Элементы математического программирования

Учебно-методический комплекс

Часть 3

Методические указания

К выполнению контрольных работ

Для студентов всех специальностей и направлений

Заочной формы обучения

 

 

УФА 2012

УДК 51(076.1)

М 54

 

 

Математика. УМК. Часть 3: Методические указания по выполнению контрольных работ для студентов заочной формы обучения / Сост.: Р.Р. Сафин, Г.А.Ларичева, М.А. Богданова. – Уфа: Уфимская государственная академия экономики и сервиса, 2012. – 79 с.

 

Приведены контрольные задания и решения типовых задач по дисциплине «Математика».

Предназначены для студентов всех специальностей и направлений заочной формы обучения.

 

Рецензент: Бакусова С.М., канд. физ.-мат. наук, доцент кафедры «Экономическая теория и мировая экономика» Уфимской государственной академии экономики и сервиса.

 

© Сафин Р.Р., Ларичева Г.А.,

Богданова М.А., 2012

© Уфимская государственная

академия экономики и сервиса, 2012

СОДЕРЖАНИЕ

 

Рекомендации по выполнению и оформлению контрольных работ 3

Введение 4

Контрольные задания 4

Список литературы 76

 

 

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Перед выполнением контрольного задания студент должен изучить со­ответствующие разделы курса по пособиям и учебникам. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию на кафедре высшей математики.

При выполнении контрольных работ надо строго придерживаться ука­занных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

1. Контрольную работу следует выполнять в тетради, отдельной для каждой работы, чернилами любого цвета, кроме красного, оставляя поля для заме­чаний рецензента.

2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины. В конце работы следует проставить дату её выполнения и расписаться.

3. В тетради должны быть решены все задачи контрольной работы строго в соответствии со своим вариантом. Контрольные работы, содержащие не все задачи, а также содержащие задачи не своего варианта, не зачитываются.

4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.

5. Перед решением каждой задачи нужно выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие зада­чи, заменить общие данные конкретными из соответствующего номера. На­пример, условие задачи 1 должно быть переписано так: Даны вершины А(1;1), В(7;4), С(4;5) треугольника. Найти: 1) длину сторо­ны АВ и т.д.

6. Решения задач следует излагать подробно и аккуратно, объясняя и мотиви­руя все действия по ходу решения и делая необходимые чертежи.

7. После получения прорецензированной работы, как незачтенной, так и за­чтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.

Если рецензент предлагает внести в решения задач те или иные исправ­ления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.

В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

Рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями ре­цензента. Прорецензированную контрольную работу вместе со всеми исправле­ниями и дополнениями, сделанными по требованию рецензента, студент пред­ставляет к защите.

ВВЕДЕНИЕ

 

В каждом семестре выполняется одна контрольная работа. Студент должен решить задачи своего варианта, который определяется по последней цифре номера зачетной книжки студента, например: если № зачетной книжки заканчивается на 2, то студент выполняет задания 1.2, 2.2, 3.2, 4.2, 5.2, 6.2, 7.2. В задачах 32-36 данные в задачах определяются по последним трем цифрам номера зачетной книжки студента.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

 

Элементы математического программирования

Задача 37. Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения линейной функции.

37.1. 37.2.

37.3. 37.4.

37.5. 37.6.

37.7. 37.8.

37.9. 37.10

Задача 38. Предположим, что для производства двух видов продукции А и В можно использовать материал только трех сортов. При этом на изготовление единицы изделия вида А расходуется кг материала первого сорта, кг материала второго сорта и кг материала третьего сорта. На изготовление единицы изделия вида расходуется кг материала первого сорта, кг материала второго сорта, кг материала третьего сорта. На складе фабрики имеется всего материала первого сорта кг, материала второго сорта кг, материала третьего сорта кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль руб., продукции вида В прибыль составляет руб.

Определить максимальную прибыль от реализации всей продукции видов А и В. Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки задачи.

38.1.

38.2.

38.3.

38.4.

38.5.

38.6.

38.7.

38.8.

38.9.

38.10.

Задача 39. Имеются три пункта поставки однородного груза пять пунктов потребления этого груза. На пунктах находится груз соответственно в количестве т. В пункты требуется доставить соответственно т груза.

Расстояние между пунктами потребления приведено в следующей матрице таблице:

 

Пункты поставки	Пункты потребления

 

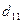
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.

39.1.

 

39.2.

 

39.3.

39.4.

39.5.

 

39.6.

 

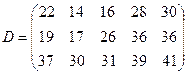
39.7.

 

39.8.

39.9.

 

39.10.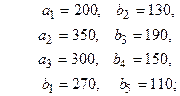

 

Решения типовых задач

Задача 37. Найти максимальное значение линейной функции при ограничениях

Решение. Построим многоугольник решений. Для этого в системе координат на плоскости изобразим граничные прямые

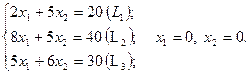
Взяв какую-нибудь, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство (эти полуплоскости на рисунке показаны стрелками). Многоугольником решений данной задачи является ограниченный пятиугольник ОАВСD.

Для построения прямой строим радиус-вектор = (50;40)=10 (5;4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора . Из рис. 1.3 следует, что опорной по отношению к многоугольнику решении эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых . Для определения её координат решим систему уравнении

Оптимальный план задачи: Подставляя значения 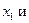в линейную функцию, получаем

 

 

8

 

А

4

 

 

 

0 D 5

 

Таким образом, для того чтобы получить максимальную прибыль в размере 260,3 руб., необходимо запланировать производство 3,9 ед. продукции и 1,7 ед. продукции

 

Задача 38. Для изготовления различных изделий А, В и С пред­приятие использует три различных вида сырья. При этом на изготовление единицы изделия вида А расходуется 18 кг материала первого вида, 6 кг материала второго вида и 5 кг материала третьего вида. На изготовление единицы изделия вида расходуется 15 кг материала первого вида, 4 кг материала второго вида, 3 кг материала третьего вида. На изготовление единицы изделия вида C расходуется 12 кг материала первого вида, 8 кг материала второго вида, 3 кг материала третьего вида. На складе фабрики имеется всего материала первого вида 360 кг, материала второго вида 192 кг, материала третьего вида 180 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 9 руб., продукции вида В прибыль составляет 10 руб., продукции вида С прибыль составляет 16 руб.

Определить максимальную прибыль от реализации всей продукции видов А, В и С. Решить задачу симплекс-методом.

Решение. Запишем данные задачи в таблицу.

Вид сырья	Нормы затрат сырья (кг) на одно изделие вида	Общее количество сырья (кг)
А	В	С
I
II
III
Прибыль от реализации единицы продукции

 

Составим математическую модель задачи. Введем новые переменные:

количество выпускаемых изделий вида А;

количество выпускаемых изделий вида В;

количество выпускаемых изделий вида С.

Так как на 1 изделие вида А предприятие расходует 18 кг сырья первого вида, то на производство общего количества продукции вида А предприятию потребуется кг того же материала. Соответственно для производства всей продукции вида В и С предприятию потребуется кг и сырья первого вида соответственно. Поскольку расходы на производство не должны превышать общего количества сырья имеющегося на складе, то при изготовлении единиц изделий вида А, единиц изделий вида 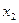В и единиц изделий вида С должно быть израсходовано не более 360 кг сырья первого вида. Таким образом, все выше сказанное можем записать в виде неравенства:

Аналогично, при затратах, на производство продукции вида А, В и С, сырья второго и третьего сорта предприятие должно учитывать количество данного сырья, имеющегося на складе. Т.е. необходимо выполнение следующих неравенств:

При этом так как количество изготовляемых изделий не может быть отрицательным, то

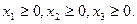
Далее, если будет изготовлено единиц изделий вида А, единиц изделий вида 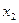В и единиц изделий вида С, то прибыль от их реализации составит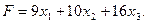

Таким образом, приходим к следующей математической задаче:

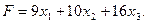(1)

(2)

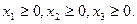
среди всех неотрицательных решений системы нера­венств (2) требуется найти такое, при котором функция (1) принимает максимальное значение.

Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-нера­венств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

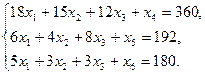
Эти дополнительные переменные означают не используемое при данном плане производства количество сырья того или иного сорта (например, - неиспользуемое количество материала I вида).

Преобразованную систему уравнений запишем в векторной форме:

где ; ; ; ; ; .

Поскольку среди векторов 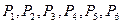имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план Х=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов , которые образуют базис трехмерного век­торного пространства.

Составляем симплексную таблицу для I итерации (табл. 1.1). В столбец записываем коэффициенты при базисных векторах в целевой функции. Коэффициенты 4-й строки вычисляются по формулам: и проверяем исходный опорный план на оптимальность:

 

 

Таблица 1.1

	Базис
			360
				-9	-10	-16

 

Как видно из табл. 1.1, значения всех основных переменных равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение це­левой функции равно нулю (т. е. стоимость произведенной про­дукции отсутствует). Этот план, конечно, не является оптималь­ным.

Это видно и из 4-й строки табл. 1.1, так как в ней имеется три отрицательных числа: . Отрицательные числа не только свидетельствуют о воз­можности увеличения общей стоимости производимой продук­ции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции. Так, число -9 означает, что при включении в план произ­водства одного изделия А обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по од­ному изделию В и С, то общая стоимость изготовляемой про­дукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отри­цательное число стоит в 4-й строке столбца вектора Р₃. Сле­довательно, в базис введем вектор . Определяем вектор, под­лежащий исключению из базиса. Для этого находим для т.е.

Найдя число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С пред­приятие может изготовлять с учетом норм расхода и имеющих­ся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно , т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, вектор подлежит исключению из базиса. Столбец вектора и 2-я строка являются направляющими. Элемент, стоящий на пересечении столбца и 2-й строки, называется разрешающим элементом. Составляем таблицу для II итерации (табл. 1.2).

 

Таблица 1.2

	Базис
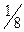
					-2

 

Сначала заполняем строку вектора, вновь введенного в ба­зис, т.е. строку, номер которой совпадает с номером направ­ляющей строки. Здесь направляющей является 2-я строка. Эле­менты этой строки табл. 1.2 получаются из соответствующих элементов табл. 1.1 делением их на разрешающий элемент (т.е. на 8). При этом в столбце записываем коэффициент , стоящий в столбце вводимого в базис вектора . Затем запол­няем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноимен­ных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.

Для определения остальных элементов табл. 1.2 применяем правило прямоугольника:

a c

d

b , где - пересчитанный коэффициент новой таблицы,

d – разрешающий элемент,

b, c – элементы, стоящие на диагонали прямоугольника.

Вычислим элементы табл. 1.2, стоящие в столбце вектора Первый из них находится в 1-й строке этого столбца. Получаем:

; записываем его в 1-й строке столбца вектора табл. 1.2.

Второй элемент столбца вектора табл. 1.2 был уже вычис­лен ранее. Вычисляем третий элемент столбца вектора : . Число 108 записываем в 3-й строке столбца вектора табл. 1.2.

Значение в 4-й строке столбца этого же вектора можно найти двумя способами:

1) по формуле ,т.е.

2) по правилу прямоугольника; в данном случае прямоугольник образован числами 0, 192, 8, -16. Этот способ приводит к тому же результату: .

Аналогично пересчитываем оставшиеся элементы табл. 1 и записываем их в новую табл. 2.

По окончании расчета всех элементов табл. 1.2 в ней полу­чены новый опорный план и коэффициенты разложения векторов через базисные векторы и значения .Как видно из этой таблицы, новым опорным планом задачи является план . При данном плане производства изготовляется 24 изделия С и остается неисполь­зованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора табл. 1.2. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели зна­чительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, на­пример, возьмем данные столбца вектора Число во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и в 1-й и 3-й строках вектора пока­зывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия B, а число -2 в 4-й строке показывает, что если будет запланирован вы­пуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными слова­ми, если включить в план производства продукции одно изде­лие В, то это потребует уменьшения выпуска изделия С на ед. и потребует дополнительных затрат 9 кг сырья I вида и кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и выступают как бы новыми «норма­ми» затрат сырья I и III вида на изготовление одного изделия В (как видно из табл. 1.1, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.

Такой же экономический смысл имеют и данные столбца век­тора табл. 1.2. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора . Число 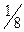во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на 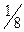ед. Одновременно потребовалось бы дополнительно кг сырья I вида и кг сырья III вида. Увеличение выпуска изделий С на 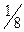ед. приведет к росту выпуска продукции на 2 руб.

Из изложенного выше экономического содержания данных табл. 1.2 следует, что найденный на II итерации план задачи не является оптимальным. Это видно и из 4-й строки табл. 1.2, поскольку в столбце вектора этой строки стоит отрицатель­ное число -2. Значит, в базис следует ввести вектор , т. е. в новом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется для 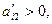т.е. находим .

Следовательно, исключению из базиса подлежит вектор , иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющих­ся объемов этого сырья предприятию следует изготовить 8 изде­лий В. Число 9 является разрешающим элементом, а столбец вектора и 1-я строка табл. 1.2 являются направляющими. Составляем таблицу для III итерации (табл. 1.3).

 

Таблица 1.3

	Базис

 

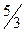
В табл. 1.3 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора . Элементы этой строки получаем из элементов 1-й строки табл. 1.2 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце данной строки записываем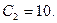

Затем заполняем элементы столбцов векторов базиса и по правилу прямоугольника вычисляем элементы остальных столб­цов. В результате в табл. 3 получаем новый опорный план и коэффициенты разложения векторов через базисные векторы и соответствующие значения

Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку табл. 1.3. В этой строке среди чисел нет отрицательных. Это означает, что найден­ный опорный план является оптимальным и

Следовательно, план выпуска продукции, включающий из­готовление 8 изделий В и 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.

Оптимальным планом производства продукции не предусмат­ривается изготовление изделий А. Введение в план выпуска про­дукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора , где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению об­щей величины стоимости на 5 руб.

Ответ: максимальная прибыль от реализации всей продукции составляет 400 руб.

Задача 39

1) На три базы поступил однородный груз в ко­личествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения соответственно в количествах 60, 70, 120, 130 и 100

Поделиться:

Воспользуйтесь поиском по сайту: