Понятие нечетких множеств и нечеткой логики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К выполнению лабораторной работы

по дисциплине "Неклассические логики"

на тему "Построение нечеткой аппроксимирующей системы"

(теория и варианты заданий) для студентов направления: 230100.62 «Информатика и вычислительная техника»,

профиль «Автоматизированные системы обработки информации и управления»,

профиль «Системы автоматизированного проектирования»

форма обучения: очная, заочная

 

Ижевск 2013

 

 

Составители: Исенбаева Е.Н., старший преподаватель кафедры АСОИУ,

Шибанова Ю.В., старший преподаватель кафедры АСОИУ.

 

 

Рекомендовано к изданию на заседании кафедры «Автоматизированные системы обработки информации и управления» ИжГТУ (протокол № от).

 

 

Исенбаева Е.Н., Шибанова Ю.В. Методические указания к выполнению лабораторной работы по дисциплине «Неклассические логики» на тему «Построение нечеткой аппроксимирующей системы» (теория и варианты заданий).- Ижевск: Издательство ИжГТУ, 2013 г.- с.

 

В методических указаниях приведено описание понятия нечетких множеств и нечеткой логики. Описаны алгоритмы нечеткого логического вывода, подробно рассмотрен алгоритм Sugeno. Приведен пример построения нечеткой аппроксимирующей системы. Методические указания содержат варианты заданий на лабораторную работу.

 

Учебное пособие предназначено для студентов очной и заочной формы обучения, направления 230100.

 

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ. 4

1. Понятие НЕЧЕТКИХ МНОЖЕСТВ И НЕЧЕТКОЙ ЛОГИКИ.. 5

2. Нечеткий логический вывод.. 7

3. ОПИСАНИЕ АЛГОРИТМА СУГЕНО.. 8

4. ПРИМЕР ПОСТРОЕНИЯ НЕЧЕТКОЙ АППРОКСИМИРУЮЩЕЙ СИСТЕМЫ 13

5. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ.. 21

6. ГЛОССАРИЙ.. 22

7. ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ.. 23

СПИСОК ЛИТЕРАТУРЫ.. 25

 

 

ВВЕДЕНИЕ

Данные методические указания предназначены для использования студентами при выполнении лабораторной работы на тему «Построение нечеткой аппроксимирующей системы». В пособии дается описание понятий нечетких множеств и нечеткой логики. Описаны алгоритмы нечеткого логического вывода. Приведен пример построения нечеткой аппроксимирующей системы.

В работе приведены варианты заданий на лабораторную работу.

Выполняя данную работу, студент должен научиться решать задачи нечеткой логики и применять полученные навыки при выполнении курсовых работ и выпускной квалификационной работы.

Понятие НЕЧЕТКИХ МНОЖЕСТВ И НЕЧЕТКОЙ ЛОГИКИ

 

Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MF_c(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MF_c(x)/x}, MF_c(x) [0,1]. Значение MF_c(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.

Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.

Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.

Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:

· названия;

· множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;

· универсального множества X;

· синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;

· семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.

Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности.

Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:

При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).

Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):

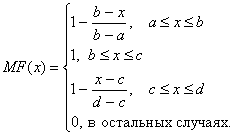
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.

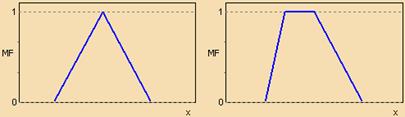
Рис. 1.1. Типовые кусочно-линейные функции принадлежности.

Функция принадлежности гауссова типа описывается формулой

и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр отвечает за крутизну функции.

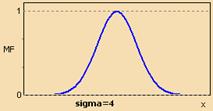
Рис. 1.2. Гауссова функция принадлежности.

Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике

 

Количество термов в лингвистической переменной редко превышает 7.

 

Нечеткий логический вывод

 

Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме "Если-то" и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:

1. Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.

2. Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечетких правил.

Пусть в базе правил имеется m правил вида:

R₁: ЕСЛИ x₁ это A₁₁ … И … x_n это A_1n, ТО y это B₁

…

R_i: ЕСЛИ x₁ это A_i1 … И … x_n это A_in, ТО y это B_i

…

R_m: ЕСЛИ x₁ это A_i1 … И … x_n это A_mn, ТО y это B_m,

где x_k, k=1..n – входные переменные; y – выходная переменная;

A_ik – заданные нечеткие множества с функциями принадлежности.

Результатом нечеткого вывода является четкое значение переменной y^* на основе заданных четких значений x_k, k=1..n.

В общем случае механизм логического вывода включает четыре этапа:

· введение нечеткости (фазификация),

· нечеткий вывод,

· композиция и приведение к четкости, или дефазификация (см. рис. 2.1).

Рис. 2.1. Система нечеткого логического вывода

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.

 

ОПИСАНИЕ АЛГОРИТМА СУГЕНО

 

Формально алгоритм Сугено,предложенный Сугено и Такаги, может быть определен следующим образом.

1. Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукций в форме:

ПРАВИЛО: ЕСЛИ «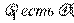» И «», ТО «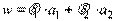», (3.1)
где , 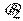– некоторые весовые коэффициенты. При этом значение выходной переменной в заключении определяется как некоторое действительное число.

2. Фазификация входных переменных. Фазификация выполняется одинаково во всех методах нечеткого вывода. Фазификацию еще называют введением нечеткости.
Целью этапа фазификации является установление соответствия между конкретным (обычно – численным) значением отдельной входной переменной системы нечеткого вывода и значением функции принадлежности соответствующего ей терма входной лингвистической переменной.

После завершения этого этапа для всех входных переменных должны быть определены конкретные значения функций принадлежности по каждому из лингвистических термов, которые используются в подусловиях базы правил системы нечеткого вывода.

Этап фазификации считается законченным, когда будут найдены все значения для каждого из подусловий всех правил, входящих в рассматриваемую базу правил системы нечеткого вывода. Это множество значений обозначим через .

Для иллюстрации выполнения этого этапа рассмотрим пример процесса фазификации трех нечетких высказываний: «скорость автомобиля малая», «скорость автомобиля средняя», «скорость автомобиля высокая»для входной лингвистической переменной – скорость движения автомобиля. Им соответствуют нечеткие высказывания следующего вида: «», «», «».

Предположим, что текущая скорость автомобиля равна 55 км/ч, т.е. 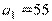км/ч.

Тогда фазификация первого нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значения 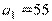км/ч в качестве аргумента функции принадлежности терма (Рис. 3.1, а).

Фазификация второго нечеткого высказывания дает в результате число 0,67 (приближенное значение), которое означает его степень истинности и получается подстановкой значения км/ч в качестве аргумента функции принадлежности терма (Рис. 3.1, б).

Фазификация третьего нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значения км/ч в качестве аргумента функции принадлежности терма (Рис. 3.1, в).

 

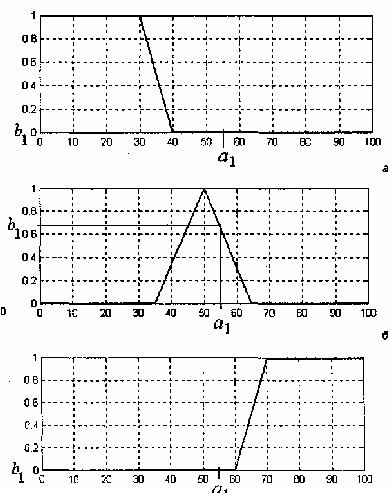Рис. 3.1. Пример фазификации входной лингвистической переменной «скорость автомобиля» для трех нечетких высказываний

3. Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min-конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

4. Активизация подзаключений в нечетких правилах продукций. Во-первых, использованием метода (3.1) находятся значения степеней истинности всех заключений правил нечетких продукций. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила. Это выполняется с использованием формулы для заключения (3.1), в которую вместо 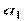и подставляются значения входных переменных до этапа фазификации. Тем самым определяются множество значений и множество значений выходных переменных – общее количество правил в базе правил.

5. Аккумуляция заключений нечетких правил продукций фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами .

6. Дефазификация выходных переменных. Используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств.

Метод центра тяжести для одноточечных множеств

 

Центр тяжести (CoGS, Centre of Gravity for Singletons) для одноточечных множеств рассчитывается по формуле:

Рис.3.2. Пример дефаззификации выходной лингвистической
переменной «скорость движения автомобиля» методом центра тяжести для одноточечных множеств.
где n – число одноточечных (одноэлементных) нечетких множеств, каждое из которых характеризует единственное значение рассматриваемой выходной переменной. Для дефазификация выходных переменных используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств:

,
где п – общее количество активных правил нечетких продукций, в подзаключениях которых присутствует выходная лингвистическая переменная .
Р исунок 3.2.- пример дефазификации выходной лингвистической
переменной «скорость движения автомобиля» методом центра тяжести для одноточечных множеств. В этом случае км/ч (приближенное значение).

 

 

Краткие теоретические сведения о пакетах программ нечетких экспертных систем

Пакеты программ, дающие возможность создавать и эксплуатировать нечеткие экспертные системы появились в начале 90-х годов. К настоящему времени известны более 100 таких пакетов. Наиболее популярны CubiCalc, FuziCalc, FuzzyTech, Fuzzy Logic Toolbox. Подробно остановимся на пакете Fuzzy Logic Toolbox.

Пакет Fuzzy Logic Toolbox (пакет нечеткой логики) - это совокупность прикладных программ, позволяющих конструировать нечеткие экспертные и/или управляющие системы [1]. Данный пакет является одним из инструментальных средств широко известной и распространенной в нашей стране математической системы MATLAB. Основные возможности пакета:

• Построение систем нечеткого вывода (экспертных систем, регуляторов, аппроксиматоров зависимостей)
• Построение адаптивных нечетких систем (гибридных нейронных сетей)
• Интерактивное динамическое моделирование в Simulink
• 
  Пакет позволяет работу:

• в режиме графического интерфейса,
• в режиме командной строки,
• с использованием блоков и примеров пакета Simulink.
  
  Ниже рассмотрены основные свойства и правила работы с пакетом Fuzzy Logic Toolbox версий 2.0.1 и 2.1, используемых, соответственно, в системах MATLAB версий 5.3 и 6.12.
  
  Графический интерфейс Fuzzy Logic Toolbox
  В состав программных средств Fuzzy Logic Toolbox входят следующие основные программы, позволяющие работать в режиме графического интерфейса:

· редактор нечеткой системы вывода Fuzzy Inference System Editor (FIS Editor или FIS-редактор) вместе со вспомогательными программами - редактором функций принадлежности (Membership Function Editor), редактором правил (Rule Editor), просмоторщиком правил (Rule Viewer) и просмоторщиком поверхности отклика (Surface Viewer);

• редактор гибридных систем (ANFIS Editor, ANFIS-редактор);
• программа нахождения центров кластеров (программа Clustering - кластеризация).

Набор данных программ предоставляет пользователю максимальные удобства для создания, редактирования и использования различных систем нечеткого вывода.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: