Экономное кодирование сообщений в отсутствие шума

 

Фактическая скорость передачи информации может быть максимальной (равной пропускной способности), если статистические характеристики источника сообщений определенным образом согласованы со свойствами информационного канала. Для каждого источника сообщений это согласование может быть достигнуто специальным выбором способа кодирования и декодирования сообщений. Такое кодирование сообщений, при котором достигается наилучшее использование пропускной способности канала связи (т.е. наибольшая скорость передачи информации), называется эффективным (или экономным).

Очевидно, что эффективное кодирование должно обеспечивать:

1) при заданной статистике источника сообщений формирование кодированных сигналов с оптимальными статистическими характеристиками, при которых достигается наибольшая скорость передачи информации;

2) возможность декодирования сигналов на приемной стороне, т.е. разделение сигналов отдельных сообщений или последовательностей сообщений, опознание этих сигналов и восстановление переданных сообщений.

Способы эффективного кодирования зависят от вида и свойств информационного канала. В настоящее время разработано большое количество различных способов эффективного кодирования, однако практическое применение пока находят лишь немногие из них. Рассмотрим примеры эффективного кодирования.

Пусть алфавит системы состоит из m символов. Средствами этого алфавита требуется представить любой из М возможных сигналов { x_i }, i = 1, М, вероятности которых { p (x_i)} заданы. Обычно М > m,поэтому каждый из сигналов, подлежащих передаче, невозможно обозначить только одним символом и приходится ставить им в соответствие некоторые последовательности символов; назовем их кодовыми слова­ми. Так как возможна последовательная передача разных кодовых слов, то они не только должны различаться для разных x_i, но и не должны быть продолжением других, более коротких. Пусть сигналу x_i соответ­ствует кодовое слово длиной m _i символов.

Операция кодирования тем более экономична, чем меньшей длины кодовые слова сопоставляются сообще­ниям. Поэтому за характеристику экономичности кода примем среднюю длину кодового слова

, (7.11)

где – длина кодового слова, сопоставляемая x_i сооб­щению.

Общие положения теории информации позволяют ука­зать оптимальные границы для средней длины L кодовых слов, которые ни при каком кодировании не могут быть уменьшены. Установим эти оптимальные границы для L из следующих соображений. Во-первых, количество ин­формации, несомое кодовым словом, не должно быть меньше количества информации, содержащегося в соот­ветствующем сообщении, иначе при кодировании будут происходить потери в передаваемой информации. Во-вто­рых, кодирование будет тем более экономичным, чем большее количество информации будет содержать в себе каждый кодовый символ; это количество информации максимально, когда все кодовые символы равновероят­ны, и равно log m. При этом i -е кодовое слово будет нести количество информации, равное .

Таким образом,

,

откуда

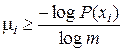. (7.12)

 

Умножив обе части последнего равенства на P (x_i)и просуммировав по всем i от 1 до п, получим

.

 

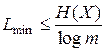Так как правая часть неравенства (7.12), как правило, не является целым числом, для достижения знака равенст­ва в нем (с учетом экономности кода) необходимо, чтобы

, (7.13)

 

где квадратными скобками обозначена целая часть числа, стоящего в них. Усредняя (7.13), получаем

.

 

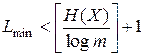Таким образом,

. (7.14)

Так, из общих соображений находим нижние границы для L и m _i.

В теории информации доказываются теоремы об условиях достижимости этих границ.

Соотношения (7.13) и (7.14) полностью отвечают на вопросы о принципиальных возможностях оптимального кодирования при отсутствии шума и являются выражением основной теоремы для дискретных систем без шума.

Приведем без доказательства фундаментальную теорему Шеннона о кодировании при отсутствии шума:

При кодировании множества сигналов с энтропией H (X) в алфавите, насчитывающем т символов, при условии отсутствия шумов, средняя длина кодового слова не может быть меньше чем H (X)/log m. Если вероятности сигналов не являются целочисленными отрицательными степенями числа т, то точное достижение указанной нижней границы невозможно; но при кодировании достаточно длинными блоками к этой границе можно сколь угодно приблизиться.

Фундаментальная теорема о кодировании при отсутствии шума является теоремой существования: она доказывает, что оптимальные коды существуют, но не дает никаких указаний на то как построить такой код.

Из теоремы однако вы­текает, что для достижения минимальной средней длины кодового слова необходимо стремиться к тому, чтобы ко­довые символы были равновероятными и статистически независимыми друг от друга. То есть для обеспечения минимальности средней длины кодового слова избыточность в кодовых словах должна быть сведена к минимуму (желательно – к нулю). Если требования независимости и равновероятности символов почему-либо невыполнимы, то, чем лучше они выполняются, тем ближе к оптимальному код.

Приведем два известных способа построения кодов, которые позволяют прибли­зиться к равновероятности и независимости кодовых символов.

1. Код Шеннона – Фано. Для составления этого кода все сообщения х_i (i = 1, 2,..., п) выписываются в порядке убывания их вероятностей (табл. 7.1).

 

Таблица 7.1

 

xi	P (xi)	Разбиение сообщений на подгруппы	Код	μ i
x 1	0,35			—	—	—
x 2	0,15			—	—	—
x 3	0,13				—	—
x 4	0,09				—	—
x 5	0,09					—
x 6	0,08					—
x 7	0,05					—
x 8	0,04
x 9	0,02

 

Записанные так сообщения затем, разбиваются на две по возможности равновероятные подгруппы. Всем сообще­ниям, входящим в первую подгруппу, приписывают циф­ру 1 в качестве первого кодового символа, а сообщениям, входящим во вторую подгруппу, – цифру 0. Аналогичное деление на подгруппы продолжается до тех пор, пока в каждую подгруппу не попадет по одному сообщению.

Убедимся, что таким образом найденный код весьма близок к оптимальному. В самом деле, энтропия сообщений

H (X) = – P (x_i) logP (x_i)» 2,75,а средняя длина кодового слова: L = m _i P (x_i)=2,84, что находится в соответствии с оптимальным характером этого кода.

Заметим, что описанный метод построения эффективного кода Шэннона-Фано может быть распространен и на коды с основанием больше двух.

2. Код Хаффмана. Для получения кода Хаффмана все сообщения выписывают в порядке убывания вероятно­стей. Две наименьшие вероятности объединяют скобкой (табл. 6.2) и одной из них приписывают кодовый символ 1, а другой 0. Затем эти вероятности складывают, ре­зультат записывают в промежутке между ближайшими вероятностями. Процесс объединения двух сообщений с наименьшими вероятностями продолжают до тех пор, пока суммарная вероятность двух оставшихся сообщений не станет равной единице. Код для каждого сообщения строится при записи двоичного числа справа налево путем обхода по линиям вверх направо, начиная с вероятности сообщения, для которого строится код.

Средняя длина кодового слова при кодировании ме­тодом Хаффмана (см. табл. 7.2) L = 2,82, что несколько меньше, чем в методе Шеннона–Фано (L = 2,84).

Таблица 7.2

 

xi	P (xi)	Объединение сообщений	Код	Pi
x 1	0,35	0,35	0,35	0,35	0,35	0,35	0,37	0,63	1,0
x 2	0,15	0,15	0,15	0,17	0,20	0,28	0,35	0,37
x 3	0,13	0,13	0,13	0,13	0,17	0,20	0,28
x 4	0,09	0,09	0,11	0,13	0,15	0,17
x 5	0,09	0,09	0,09	0,11	0,13
x 6	0,08	0,08	0,09	0,09
x 7	0,05	0,06	0,08
x 8	0,04	0,05
x 9	0,02

 

 

Согласование источника с двоичным каналом путем статистического кодирования по методу Хаффмена позволяет повысить эффективность передачи по сравнению с методом Шеннона–Фано.

Заметим, что можно синтезировать статистический код с более экономичными двоичными кодовыми комбинациями, чем в коде Хаффмена, но для разделения кодовых комбинаций будут необходимы сигналы синхронизации и поэтому эффективность передачи информации окажется все-таки хуже, чем при использовании кода Хаффмена.

До сих пор при кодировании сообщения дискретного источника предполагалось, что последний не имеет памяти. Обычно реальные источники сообщений обладают памятью, а избыточность, обусловленная памятью источника, не может быть уменьшена при независимом статистическом кодировании отдельных элементов сообщения по методикам Шеннона-Фано, Хаффмена.

Универсальным способом сокращения избыточности, в том числе обусловленной памятью источника, является укрупнение. В этом случае кодирование осуществляется длинными блоками, поскольку вероятностные связи между блоками меньше, чем между отдельными элементами сообщения. При этом вероятностные зависимости тем меньше, чем длиннее блоки.

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: