 |
Пояснения к выполнению работы.
|
|
|
|
1. С геометрической точки зрения определенный интеграл 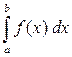 – есть площадь фигуры, ограниченной графиком функции
– есть площадь фигуры, ограниченной графиком функции  и прямыми
и прямыми  ,
,  ,
, 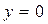 . Функция
. Функция  называется подынтегральной функцией.
называется подынтегральной функцией.
Чтобы приближенно вычислить эту площадь, разделим интервал интегрирования  на
на  равных отрезков длиной
равных отрезков длиной  каждый. Тогда координата левого конца i -го отрезка определяется по формуле
каждый. Тогда координата левого конца i -го отрезка определяется по формуле  , где
, где  ,
,  . Простейший приближенный расчет площади под кривой
. Простейший приближенный расчет площади под кривой  состоит в нахождении суммы площадей прямоугольников, у каждого из которых основание совпадает с отрезком
состоит в нахождении суммы площадей прямоугольников, у каждого из которых основание совпадает с отрезком  , а высота равна значению функции в точке
, а высота равна значению функции в точке  (метод левых прямоугольников). Можно высоту брать равной значению функции в точке
(метод левых прямоугольников). Можно высоту брать равной значению функции в точке  (метод правых прямоугольников) или в точке
(метод правых прямоугольников) или в точке  (метод центральных прямоугольников). При использовании метода левых прямоугольников формула для вычисления площади выглядит следующим образом:
(метод центральных прямоугольников). При использовании метода левых прямоугольников формула для вычисления площади выглядит следующим образом:
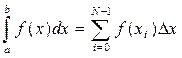 .
.
Можно повысить точность вычисления определенного интеграла, если заменить на каждом интервале  ,
,  дугу графика
дугу графика  отрезком (хордой), соединяющем точки с координатами
отрезком (хордой), соединяющем точки с координатами  и
и  . В этом случае фигура, ограниченная графиком функции и прямыми
. В этом случае фигура, ограниченная графиком функции и прямыми 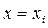 ,
,  , приближенно заменяется не прямоугольником, а трапецией, и искомый определенный интеграл рассчитывается как сумма площадей всех таких трапеций:
, приближенно заменяется не прямоугольником, а трапецией, и искомый определенный интеграл рассчитывается как сумма площадей всех таких трапеций:
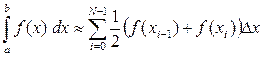 .
.
Формула может быть существенно упрощена, но мы оставим это для курса вычислительной математики (сейчас можете попытаться упростить ее самостоятельно).
2. Замена графика функции  хордами, описанная в методе трапеций, позволяет при помощи электронных таблиц довольно легко определять приближенное значение длины дуги графика
хордами, описанная в методе трапеций, позволяет при помощи электронных таблиц довольно легко определять приближенное значение длины дуги графика  на интервале
на интервале  . В этой задаче рассматриваемая кривая представляется в виде ломанной, длина s которой равна сумме длин
. В этой задаче рассматриваемая кривая представляется в виде ломанной, длина s которой равна сумме длин  её звеньев. Длину
её звеньев. Длину  звена, построенного на отрезке
звена, построенного на отрезке  , можно найти как длину гипотенузы прямоугольного треугольника с катетами, равными
, можно найти как длину гипотенузы прямоугольного треугольника с катетами, равными  и
и  , используя известную теорему Пифагора. В результате суммирования длин всех звеньев, получаем:
, используя известную теорему Пифагора. В результате суммирования длин всех звеньев, получаем:
|
|
|
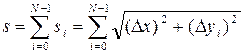 .
.
Следует отметить, что точность приближенного вычисления интегралов зависит от величины  , то есть от количества отрезков, на которые разбивается интервал интегрирования
, то есть от количества отрезков, на которые разбивается интервал интегрирования  . При отсутствии погрешностей округления, чем больше
. При отсутствии погрешностей округления, чем больше  , тем выше точность (с ростом N погрешность вычислений сходится к нулю).
, тем выше точность (с ростом N погрешность вычислений сходится к нулю).
3. В качестве примера вычислим интеграл  с точностью представления результатов вычислений до 4 знаков после запятой.
с точностью представления результатов вычислений до 4 знаков после запятой.
В ячейку А6 вводим нижнюю границу интервала интегрирования  , равную 0,5. В следующую ячейку А7 вводим значение 0,51, отстоящее от нижней границы на шаг
, равную 0,5. В следующую ячейку А7 вводим значение 0,51, отстоящее от нижней границы на шаг 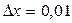 . Рекомендуется выбирать шаг в зависимости от требуемой точности вычисления интеграла. Затем выделяем обе ячейки А6 и А7. В правой нижней части выделенной области есть жирная черная точка – маркер заполнения, – тянем её мышкой вниз, пока не получим число, соответствующее верхней границе интеграла, т. е. значению
. Рекомендуется выбирать шаг в зависимости от требуемой точности вычисления интеграла. Затем выделяем обе ячейки А6 и А7. В правой нижней части выделенной области есть жирная черная точка – маркер заполнения, – тянем её мышкой вниз, пока не получим число, соответствующее верхней границе интеграла, т. е. значению  . Это достигается в ячейке А206.
. Это достигается в ячейке А206.
Выделим мышкой столбцы С, Е и G, указывая мышкой их заголовки. Вызовем с помощью правой кнопки мыши контекстное меню выделенных столбцов и выберем в нем опцию Формат ячеек. Далее, на закладке Число, выберем в качестве числового формата – Числовой и укажем отображаемое число десятичных знаков 4. Нажмем клавишу OК.
3.1. Теперь вычислим определенный интеграл с помощью метода левых прямоугольников. Для этого введем в ячейку С6 формулу =(А7-А6)*(Ln(А6)) (величина логарифма и есть высота соответствующего прямоугольника). Выделим ячейку С6 и протянем маркер заполнения вниз, до ячейки С205. Таким образом, в столбце C мы получили площади всех прямоугольников.
Выделим ячейку С206 и нажмем на кнопку Автосумма на панели Стандартные. Нажмем Enter, подтверждая этим предложенную формулу. В результате получим сумму всех выше расположенных чисел в столбце, т. е. значение интеграла, вычисленное методом прямоугольников.
|
|
|
3.2. Вычислим определенный интеграл с помощью метода трапеций. Для этого введем в ячейку Е6 следующую формулу =(А7-А6)*(Ln(А7)+Ln(А6))/2. Выделите ячейку Е6 и протяните маркер заполнения вниз до ячейки Е205. Так мы вычислили площади всех трапеций. Выделив ячейку Е206, вычислите их сумму с помощью кнопки Автосумма на панели Стандартные. Мыполучили значение интеграла, найденное методом трапеций.
3.3. Вычислим длину графика функции  на интервале [0,5; 2,5].
на интервале [0,5; 2,5].
Для вычисления длин хорд введите в ячейку G6 формулу
=((A7-A6)^2+(Ln(A7)-Ln(A6))^2)^(0,5). Выделите ячейку G6 и протяните маркер заполнения вниз до ячейки G205. В ячейке G206, используя Автосумму, найдите приближенное значение искомой длины графика.
3.4. Повторите в соседних столбцах все расчеты при меньшем шаге интегрирования, например, при шаге 0,001. Сравните результаты с полученными ранее. Проанализируйте их и сделайте выводы.
3.5. Вычисления провести по варианту и записать в отчет.
ВАРИАНТЫ ЗАДАНИЙ К РАЗДЕЛУ 1 И 2
Ниже приводятся типовые варианты заданий.
1). 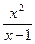 ; 1,5 ≤ x ≤3,5. 11).
; 1,5 ≤ x ≤3,5. 11).  ; 0 ≤ x ≤ 2.
; 0 ≤ x ≤ 2.
2). 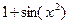 ;
;  ≤ x ≤до 5
≤ x ≤до 5  . 12).
. 12).  ; 0,5 ≤ x ≤2,5.
; 0,5 ≤ x ≤2,5.
3).  ;
;  ≤ x ≤до
≤ x ≤до  . 13).
. 13).  ; 1 ≤ x ≤ 3.
; 1 ≤ x ≤ 3.
4).  ; -2 ≤ x ≤до 1. 14).
; -2 ≤ x ≤до 1. 14).  ;
; 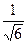 ≤ x ≤
≤ x ≤  .
.
5).  ; 4,3 ≤ x ≤до 6,8. 15).
; 4,3 ≤ x ≤до 6,8. 15).  ; 4,3 ≤ x ≤ 6,8.
; 4,3 ≤ x ≤ 6,8.
6). 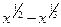 ; 0 ≤ x ≤ 4. 16).
; 0 ≤ x ≤ 4. 16).  ; 0 ≤ x ≤
; 0 ≤ x ≤  .
.
7). 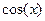 ;
;  ≤ x ≤ 2
≤ x ≤ 2  . 17).
. 17).  ; 2 ≤ x ≤4.
; 2 ≤ x ≤4.
8).  ; 5 ≤ x ≤ 8. 18).
; 5 ≤ x ≤ 8. 18).  ; 0,14 ≤ x ≤3,67.
; 0,14 ≤ x ≤3,67.
9). 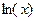 ; 0,5 ≤ x ≤ 2,5. 19).
; 0,5 ≤ x ≤ 2,5. 19).  ; 5 ≤ x ≤8.
; 5 ≤ x ≤8.
10). 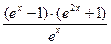 ; 5 ≤ x ≤ 8. 20).
; 5 ≤ x ≤ 8. 20). 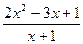 ; 5 ≤ x ≤8.
; 5 ≤ x ≤8.
|
|
|


