 |
Теорема 2 (Формула Эйлера).
|
|
|
|
,
где p j - j -ое простое число и, таким образом, бесконечное произведение справа берется по всем простым числам.
Доказательство. Пусть X ³ 1, Re(s) > 1. Ряды
абсолютно сходятся (ибо мажорируются геометрическими прогрессиями). По теореме 1 это значит, что бесконечное произведение в формуле Эйлера сходится. Имеем (значок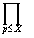 
означает произведение по всем простым числам, не превосходящим X):
.
Здесь при получении первого равенства использовалась формула суммы геометрической прогрессии, при получении последнего равенства существенную роль сыграла основная теорема арифметики. Через R (s, X) обозначен остаточный член, приписывание которого в нужном месте, вообще-то, позволяет поставить знак равенства между любыми величинами. На самом же деле, R (s, X) содержит бесконечное число слагаемых вида 1/ n s , не вошедших в стоящую перед ним сумму. Оценим остаточный член:
,
т.е. R (s, X) ® 0, при X ® ¥. Это и означает справедливость формулы Эйлера.
¨
Следствие 2. При Re(s) > 1, z (s) не имеет нулей.
Доказательство. Имеем:
,
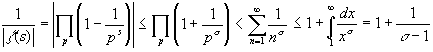значит,
.
¨
Продолжим z (s) в полуплоскость Re(s) > 0. Следующие лемма и следствие из нее призваны лишь показать один из возможных способов реализации такого продолжения, поэтому их доказательство можно пропустить без всякого ущерба для дальнейшего понимания.
Лемма 1. При Re(s) > 0, N ³ 1
Доказательство. Имеем при Re(s) > 1:
Но последний интеграл справа определяет аналитическую функцию даже при Re(s) > 0. Поэтому, в силу принципа аналитического продолжения, утверждение леммы 1 справедливо.
¨
Следствие 3. Функция z (s) является аналитической в полуплоскости Re(s)>0 за исключением точки s = 1; в точке s = 1 дзета-функция имеет простой полюс с вычетом, равным 1.
|
|
|
¨
Оказывается, что дзета-функция имеет бесконечно много нулей в "критической полосе" 1 > Re(s) > 0. Известно, что эти нули лежат симметрично относительно прямых Re(s) =1/2 и Im(s) = 0; известно, что в области Re(s) ³ 
, где b = Im(s), а с - абсолютная постоянная, нулей у z (s) нет (Теорема Ш. Валле-Пуссена). Однако знаменитая гипотеза Римана о том, что все нули z (s) лежат на прямой Re(s) = 1/2 до сих пор не доказана, хотя проверена для более 7 миллионов корней. Хотите посмотреть на первые десять корней z (s) = 0? Вот они:
r 1,2=1/2±14,134725 i,
r 3,4=1/2±21,022040 i,
r 5,6=1/2±25,010856 i,
r 7,8=1/2±30,424878 i,
r 9,10=1/2±32,935057 i.
(Шутка: предлагаю непосредственной подстановкой убедиться, что это - корни z (s) = 0.)
Приведу еще, в качестве красивой картинки, без комментариев, ту самую удивительную формулу Римана, о которой уже упоминалось в этом пункте мелким шрифтом, для числа p (x) простых чисел, не превосходящих x:
,
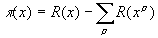где суммирование справа ведется по всем нулям z (s), а
.
К сожалению, рассказ о серьезных и нетривиальных применениях дзета-функции Римана выходит за рамки этой скромной книжки, поэтому, чтобы хоть как-то представить всю мощь этой функции, немного постреляем из пушки по воробьям - докажем с ее помощью пару известных утверждений.
Утверждение 1. Простых чисел бесконечно много.
Доказательство первое. Ну пусть p 1 , p 2 ,..., p k - все простые. Тогда, так как
,
получаем (при s = 1 и достаточно больших N):
,
ибо 
.
Но это невозможно, ибо гармонический ряд
расходится.
¨
Доказательство второе. Ну пусть p 1 , p 2 ,..., p k - все простые.
Тогда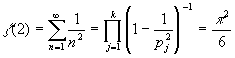 
, что невозможно, ибо конечное произведение суть рациональное число, чего никак не скажешь о числе p 2/6.
¨
Следующее утверждение гораздо менее известно, чем бесконечность множества простых. Возмем гармонический ряд и сильно проредим его, оставив в нем только слагаемые, обратные к простым числам и выкинув все слагаемые, являющиеся обратными к составным. Это действительно сильное прорежение, так как в натуральном ряде имеются сколь угодно длинные промежутки без простых чисел, например:
|
|
|
n! + 2, n! + 3, n!+4,..., n! +n.
Гармонический ряд, как известно, расходится. Удивительно, что
Утверждение 2. Ряд 
из обратных величин ко всем простым числам расходится.
Доказательство. Пусть X Î N. Имеем:
где значок Ñ означает, что суммирование ведется по всем n> X, в разложении которых нет простых сомножителей, больших Х. Значит:
и 
,
так как гармонический ряд расходится. Из последнего вытекает, что бесконечное произведение
- расходится к нулю, т.е.
.
Значит,
.
Мы помним замечательный предел:
,
из которого следует, что:
,
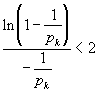откуда моментально:
.
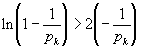Таким образом, в ряде
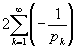
каждый член меньше соответствующего члена расходящегося к - ¥ ряда
,
следовательно, ряд
расходится к + ¥.
¨
Справедливости ради отмечу: несмотря на то, что ряд самым невероятным образом расходится, он расходится все-таки медленнее гармонического. Про частичные суммы этих рядов известно, что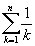 
растет как ln n, (1) в то время, как
растет только как ln(ln p n ).
Позвольте мне быстренько закончить этот уже порядком поднадоевший пункт, а вместе с ним и весь третий параграф, установлением связи между дзета-функцией (которая не мультипликативна) и функцией Мебиуса m (n) (которая мультипликативна). Из этой связи понятно, что z (s) очень близка к мультипликативным функциям - просто единица, деленная на дзета-функцию, есть сумма (правда, бесконечная) мультипликативных функций.
Лемма 2. Пусть Re(s) > 1. Тогда:
Доказательство. Пусть n 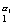= p 
p 
· · · p 
. В лемме 1 из пункта 14 положим q (x)=1/ xs - мультипликативная функция. Тогда:
,
,
где значок Ñ, как и ранее означает, что суммирование ведется по всем n > X, в разложении которых нет простых сомножителей, больших Х. Далее, устремляя Х к бесконечности и вспоминая определение функции Мебиуса, получаем:
,
следовательно:
.
¨
Конечно, пункт 15 получился великоватым, поэтому на экзамене я не буду спрашивать его целиком - радуйтесь, ребятишки! Однако, если вы будете плохо себя вести: плеваться из трубочек на лекциях жеванными бумажками и тащить с пола в рот всякую гадость, то я спрошу на экзамене этот пункт целиком и, как следствие, поставлю двойку.
|
|
|
Завершим этим мажорным аккордом наше знакомство с дзета-функцией, а вместе с этим знакомством завершается и весь третий параграф. Ура!
Задачки 
| 1. Сделайте что угодно, но вычислите z (3), после чего можно пойти погулять.
2. Докажите, что ряд, составленный из обратных величин к простым числам, встречающимся в арифметической прогрессии 3, 7, 11, 15, 19, 23,..., расходится.
3. Пусть L (a) = ln p для a = p l , где p - простое, l - натуральное; L (a) = 0 для остальных натуральных а. (2) Докажите, что при Re(s) > 1 выполнено:
 .
4. Пусть Re(s) > 2. Докажите, что
 ,
где j (n) - функция Эйлера.
5. Определим вероятность Р того, что k натуральных чисел x 1 , x 2 , …, x k будут взаимно простыми, как предел при N ®¥ вероятности P N того, что будут взаимно простыми k чисел x 1 , x 2 , …, x k , каждому из которых независимо от остальных присвоено одно из значений 1, 2,..., N, принимаемых за равновозможные. (3) Докажите, что P =1/z(k).
|
(1) Более того, известен поразительный результат Л. Эйлера о том, что предел 
существует и g»0,5772.... Число g называется теперь постоянной Эйлера.
(2) Функция L(a) называется функцией Мангольдта - весьма примечательный персонаж в теории чисел, знакомство с которым осталось, к сожалению, за рамками этой книжки.
(3) Сравните с определением, данным в пункте 3 этой книжки. Обратите внимание, что результат пункта 3 - теорема Чезаро - находится в прекрасном соответствии с утверждением этой задачи: P =6/p2=1/z(2).
Путь к решению этой весьма сложной задачи станет полегче, если вы докажете предварительно следующий факт:
Пусть k>1 и заданы системы x 1(1), x 2(1),..., xk (1); x 1(2), x 2(2),..., xk (2); x 1(n), x 2(n),..., xk (n) целых чисел, не равных одновременно нулю. Пусть, далее, для этих систем однозначно определена некоторая (произвольная) функция f (x 1, x 2, xk). Тогда
,
где: m - функция Мебиуса, SÑ обозначает сумму значений f (x 1, x 2,... xk), распространенную на системы взаимно простых чисел, Sd обозначает сумму значений f (x 1, x 2,... xk), распространенную на системы чисел, одновременно кратных d, а d пробегает натуральные числа.
Теория сравнений
Эпиграфом к этому параграфу могла бы послужить крылатая фраза "Все познается в сравнении!", но я сознательно отказался от обыкновения писать эпиграфы к каждому параграфу, так как мне неохота их выдумывать. В этом параграфе мы займемся изучением арифметики в кольцах вычетов – в объектах, хорошо знакомых еще из начального университетского курса алгебры. При этом мы будем пользоваться преимущественно терминологией и традиционными теоретико-числовыми обозначениями, нежели обозначениями и терминологией теории колец – такова традиция элементарного изложения этой теории для школьников десятого класса и студентов математико-механического факультета третьего и четвертого курсов. Эта традиция имеет железное обоснование: школьники понятия кольца еще не знают, студенты понятие кольца уже забыли. Но и те, и другие счастливы.
|
|
|
|
|
|
