 |
Основные свойства неопределенного интеграла.
|
|
|
|
1. 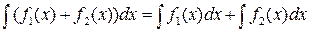
2. 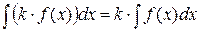
3. 
4. 
Основные методы интегрирования
1. Метод непосредственного интегрирования.
2. Метод замены переменной (метод подстановки) заключается во введении новой переменной интегрирования. При этом заданный интеграл сводится к новому, который является табличным.
 (35)
(35)
3. Интегрирование по частям.
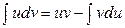 (36)
(36)
Выделяют два типа интегралов, берущихся по частям:
1)  ;
;  ;
; 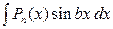 ;
; 
Здесь за u принимают многочлен 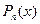 , а за
, а за  – остальные сомножители.
– остальные сомножители.
2)  ;
; 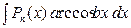 ;
;  ;
;
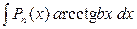
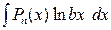
Здесь за  принимают
принимают  , а за u – остальные сомножители.
, а за u – остальные сомножители.
4. Интегрирование рациональных дробей
Рациональной дробью называется функция, равная отношению двух многочленов, т.е. 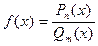 . Для интегрирования рациональной дроби необходимо представить ее в виде суммы простейших дробей видов:
. Для интегрирования рациональной дроби необходимо представить ее в виде суммы простейших дробей видов:
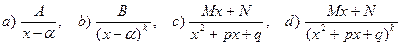 ,
,
где k, – целое положительное число, а трехчлен 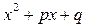 не имеет действительных корней.
не имеет действительных корней.
Если дробь  неправильная, то необходимо выделить целую часть дроби.
неправильная, то необходимо выделить целую часть дроби.
5. Интегрирование некоторых тригонометрических функций
Для нахождения интегралов типа  используют:
используют:
a) формулы понижения степени:
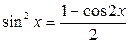 ,
,  (37)
(37)
b) подстановку  , если n – нечетное;
, если n – нечетное;
c) подстановку 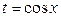 , если m – нечетное/
, если m – нечетное/
Для нахождения интегралов вида 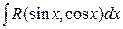 , где R – рациональная функция, используют универсальную подстановку:
, где R – рациональная функция, используют универсальную подстановку: 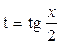 , при этом.
, при этом.
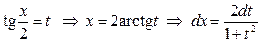 ,
, 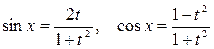 (38)
(38)
Тема Интегральное исчисление функции одной переменной.
Определенный интеграл.
1. Формула Ньютона–Лейбница
Если функция 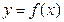 непрерывна на
непрерывна на 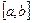 и
и 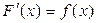 , то имеет место формула:
, то имеет место формула:
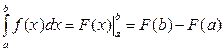 , (39)
, (39)
2. Несобственные интегралы первого и второго рода
Несобственные интегралы первого рода:
 ,
,

Несобственные интегралы второго рода:
 , где a – точка бесконечного разрыва функции
, где a – точка бесконечного разрыва функции  , и
, и
 , где b – точка бесконечного разрыва функции
, где b – точка бесконечного разрыва функции  .
.
Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
|
|
|
3. Вычисление площади фигуры
Криволинейной трапецией в называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой 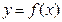 .
.
Формула для вычисления площади криволинейной трапеции:
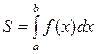 (40)
(40)
4. Вычисление объема тела вращения
Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b, y = 0 и кривой 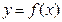 вращается вокруг оси ОX. Объем полученного при этом тела вращения вычисляется по формуле:
вращается вокруг оси ОX. Объем полученного при этом тела вращения вычисляется по формуле:
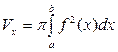 (41)
(41)
Тема Функции многих переменных
Функция f есть функция двух переменных x и y, если каждой паре  значений из некоторого множества D соответствует определённое значение величины f. Множество D называется областью определения функции
значений из некоторого множества D соответствует определённое значение величины f. Множество D называется областью определения функции  .
.
Если одной из переменных функции  придать приращение, а другую переменную не изменять, то функция получит частное приращение по одной из переменных:
придать приращение, а другую переменную не изменять, то функция получит частное приращение по одной из переменных: 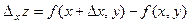 и
и 
Частной производной функции нескольких переменныхназывается предел отношения частного приращения функции к соответствующему приращению переменной при условии, что приращение переменной стремится к нулю:
 – частная производная функции z по переменной x;
– частная производная функции z по переменной x;
 – частная производная функции z по переменной у.
– частная производная функции z по переменной у.
При вычислении частной производной по одной переменной, все остальные переменные следует считать постоянными и проводить дифференцирование по правилам дифференцирования функции одной переменной.
Полный дифференциал функции  выражается формулой:
выражается формулой:
 (42)
(42)
Производные ФНП высших порядков
Так как 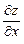 и
и 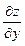 являются функциями переменных x и y, то их можно дифференцировать по x и по y. Эти частные производные от функции
являются функциями переменных x и y, то их можно дифференцировать по x и по y. Эти частные производные от функции  называются частными производными второго порядка
называются частными производными второго порядка
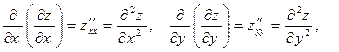

Экстремумы ФНП
Функция  имеет максимум в точке
имеет максимум в точке 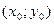 , если существует такая окрестность точки
, если существует такая окрестность точки 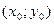 , в которой выполнено неравенство
, в которой выполнено неравенство  для всех точек
для всех точек  из этой окрестности, отличных от
из этой окрестности, отличных от 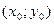 .
.
|
|
|
Функция  имеет минимум в точке
имеет минимум в точке 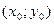 , если существует такая окрестность точки
, если существует такая окрестность точки 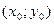 , в которой выполнено неравенство
, в которой выполнено неравенство  для всех точек
для всех точек  из этой окрестности, отличных от
из этой окрестности, отличных от 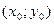 .
.
Максимум 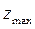 и минимум
и минимум  называют экстремумами ФНП.
называют экстремумами ФНП.
Необходимое условие экстремума ФНП: если функция  имеет экстремум в точке
имеет экстремум в точке 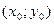 , то ее частные производные первого порядка в этой точкеравны нулю.
, то ее частные производные первого порядка в этой точкеравны нулю.
Точки, в которых выполняется необходимое условие, называются критическими точками функции.
Достаточное условие экстремума ФНП: Вычислим в критической точке 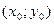 значения
значения  ,
, 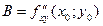 ,
,  . Обозначим
. Обозначим 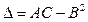 . Значение
. Значение 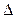 показано в таблице 5.
показано в таблице 5.
Таблица 5
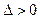
| 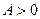

| В точке 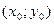 минимум
В точке минимум
В точке 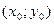 максимум максимум
|

| В точке 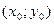 функция экстремума не имеет функция экстремума не имеет
| |

| В точке 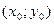 экстремум может быть, а может не быть. Необходимы дополнительные исследования. экстремум может быть, а может не быть. Необходимы дополнительные исследования.
|
|
|
|


