Определение натуральной величины (н.в.) отрезка прямой общего положения и углов наклона его к плоскостям проекций

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

 

 

Утверждено на заседании

кафедры начертательной

геометрии и черчения

12 ноября 2011 года

 

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению работ по

начертательной геометрии

 

Квалификация выпуска «Бакалавр»

 

 

Ростов-на-Дону 2011

 

УДК 514

 

Задания и методические указания к выполнению работ по начертательной геометрии (для студентов заочной формы обучения, квалификация выпуска «Бакалавр»). – Ростов – на – Дону: Рост. гос. строит. ун-т, 2011. – 20 с.

Даны исходные данные и методические указания к выполнению контрольных работ по начертательной геометрии для студентов заочной формы обучения.

 

 

Составители: Н.В. Ковалева,

О.А. Арцишевская

Редактор Н.Е. Гладких Темплан 2011 г., поз. 141.

ЛР020818 от. Подписано в печать. Формат 60х84/16 Бумага писчая. Ризограф. Уч.-изд. л. 1,5. Тираж экз. Заказ ________

Редакционно-издательский центр Ростовского государственного строительного университета. 344022, Ростов н/Д, ул. Социалистическая, 162

 

Ó Ростовский государственный

строительный университет, 2011

 

В процессе изучения начертательной геометрии студенты – заочники ускоренной формы обучения выполняют 2 контрольные работы.

Каждая контрольная работа по начертательной геометрии состоит из нескольких задач, часть из которых выполняется по индивидуальным вариантам. Вариант должен соответствовать последней цифре шифра.

Каждая задача выполняется на отдельном формате чертежной бумаги преимущественно формата А4 и частично - А3. Рекомендации по выбору формата А3 даны в комментариях к задачам. Если о формате не говорится ничего, следует применять формат А4. Поле чертежа ограничивается рамкой: слева - 20 мм от обреза листа, с других трех сторон - 5 мм. Внизу, вплотную к рамке (для формата А3 - в правом нижнем углу), помещается основная надпись размером 15><185 (рис.1).

РГСУ ЗПГС - 191 - 340058 К.Р. №…, З.№… Иванов А.П.

 

Название Номер Шифр Номер контрольной Номер Ф.И.О.

университета группы работы задачи студента

Рис.1

Все чертежи должны быть оформлены в соответствии с требованиями ГОСТов ЕСКД. Надписи и буквенно - цифровые обозначения на листах и в основной надписи должны выполняться стандартным шрифтом. Для придания наглядности решению желательно обводить: исходные данные - черным; линии построения - синим, зеленым; искомые линии, являющиеся окончательным решением, - красным. Все линии графических построений должны сохраняться. Не принимаются чертежи неаккуратные, неправильно оформленные, без четких графических построений.

Контрольные работы представляется в сброшюрованном виде и оформляются титульным листом с выходными данными студента.

Работы должны быть защищены автором до экзамена. Преподаватель вправе аннулировать представленные контрольные работы, если при собеседовании убедится, что студент выполнил их несамостоятельно.

 

Контрольная работа №1 содержит два раздела:

Первый раздел: решение позиционных и метрических задач без применения методов преобразования проекций (задачи 1 - 4).

Второй раздел: метод замены плоскостей проекций (задачи 5 - 7).

Контрольная работа №2: поверхности, их пересечение с прямой, плоскостью, а также между собой (задачи 8 - 13).

Содержание задач

Контрольная работа №1

Первый раздел. Данные для выполнения задач 1 - 7 следует брать из табл.1 в соответствии с вариантом. Координаты точек даны в мм.

1. Построить эпюры точек A, B, C. D. Через точку A провести горизонталь h под углом 45 градусов к фронтальной плоскости проекций. Отложить на построенной горизонтали от точки A отрезок, равный 50мм. Через точку B провести фронталь f под углом 30 градусов к горизонтальной плоскости проекций. Отложить на построенной фронтали от точки B отрезок, равный 40мм. Через точку C провести прямую общего положения и определить углы ее наклона к горизонтальной и фронтальной плоскостям проекций.

2. Определить расстояние от точки C горизонтали. Построить точку N, симметричную точке C относительно фронтали (данные взять из задачи 1).

3. Определить точку пересечения прямой общего положения (произвольной) с плоскостью треугольника ABC.

4. Определить расстояние от точки D до плоcкости, заданной точками A, B, C.

Второй раздел. Методом замены плоскостей проекций решить задачи 5 -7.

Ввиду громоздкости построений исходные данные к этим задачам рекомендуется вычерчивать в масштабе уменьшения и использовать формат А3.

5. Определить расстояние от точки A до прямой общего положения (данные взять из задачи 1).

6. Определить расстояние от точки D до плоcкости, заданной точками A, B, C.

7. Определить натуральную величину треугольника ABC.

Таблица 1

Вари- ант	Точки	X	Y	Z	Вари- ант	Точки	X	Y	Z
	A B C D					A B C D
	A B C D					A B C D
	A B C D					A B C D
	A B C D					A B C D
	A B C D					A B C D

Контрольная работа №2

Данные для выполнения задач 8 - 13 следует брать из табл.2 независимо от варианта. Цифры, стоящие в углах, соответствуют номерам задач. Для лучшей наглядности исходные данные к этим задачам рекомендуется вычерчивать в масштабе увеличения.

8, 9, 10. Найти точки пересечения прямой общего положения с поверхностью.

11. Найти линию пересечения плоскости общего положения с поверхностью.

12, 13. Построить линию пересечения поверхностей.

Таблица 2

 

 

Методические указания к выполнению контрольных работ

Контрольная работа №1

Первый раздел

 

1. Построить точку по координатам (к задаче №1) (рис.1)

 

А(4,3,2)

А(x, y, z)

 

 

Рис.1

2. Горизонталь - это прямая, параллельная горизонтальной плоскости проекций П₁ (рис.2).

 

h₂ || X, h₁ || X.

На плоскость П₁ горизонтальная проекция горизонтами (h₁) проецируется в натуральную величину (н.в.).

Любой отрезок, взятый на горизонтали, на П₁ (h₁) спроецируется в н.в.

 

Например:на горизонтали отложить отрезок АВ=30 мм (А­₁В₁= 30 мм ® А₂В₂).

b - угол наклона горизонтали к фронтальной плоскости проекции П₂

b = h^ÙП₂; b_П2 = h₁^ÙX.

 

3. Фронталь - это прямая, параллельная фронтальной плоскости проекции (рис.3). f₁ || X, f₂ || X.

 

Любой отрезок, взятый на фронтали, спроецируется на П₂ в натуральную величину.

Например: на фронтали отложить отрезок СД=20 мм (рис. 3).

С₂Д₂ =20 мм ® С₁Д₁ ,

 

a - угол наклона фронтали к горизонтальной плоскости проекции П₁,

a = f ^ÙП₁; a_П1 = f₂^ÙX.

 

 

4. Прямая общего положения - это прямая не || и не ^ ни одной из плоскостей проекции (рис. 4).

Обе её проекции расположены под произвольными углами к оси Х.

Поскольку эта прямая не || ни одной из плоскостей проекции, то любой отрезок, взятый на этой прямой, не спроецируется в н.в., а в задачах необходимо определять н.в. отрезка общего положения.

 

Определение натуральной величины (н.в.) отрезка прямой общего положения и углов наклона его к плоскостям проекций

Н.в. отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, один катет которого равен длине одной из проекций этого отрезка, а другой катет (рис. 5) равен разности расстояний концевых точек другой проекции отрезка от оси Х (DZ) (рис. 6).

 

 

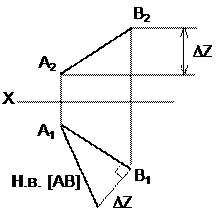Рис.5 Рис.6

 

Угол наклона прямой общего положения к плоскости проекций равен углу между н.в. отрезка прямой и проекцией прямой на соответствующую плоскость проекций (рис. 7).

 

 

b_П2=E₂F₂^ÙН.в.[EF]

 

 

 

Рис. 7

Теорема о проецировании прямого угла (к задаче №2)

При ортогональном проецировании прямой угол проецируется в прямой, если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна этой плоскости. Из теоремы следует, что одной из сторон прямого угла является линия уровня (горизонталь, фронталь) (рис.8).

 

 

 

Ð ВАС = 90^о Ð EDF = 90^о

Ð В₁А₁С₁ = 90^о Ð E₂D₂F₂ = 90^о

Ð В₂А₂С₂ ¹ 90^о Ð E₁D₁F₁ ¹ 90^о

Рис. 8

Построить точку, симметричную (×) М относительно горизонтали (рис.9).

План:

1. Опустить из (×) М перпендикуляр на горизонталь МО^h,

М₂О₂^h₁ ® М₁О₁.

2. На продолжении ^ отложить отрезок, равный полученному МО=NO.

М₁О₁=O₁N₁;

М₂О₂=O₂N₂.

 

 

Рис. 9

Найти расстояние от точки К до фронтали (рис. 10).

План:

1. Опустить ^ из (×) К на фронталь

КО ^ f;

К₂О₂ ^ f₂ ® K₁O_1.

2. Найти н.в. отрезка ОК.

 

Рис. 10

 

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: