 |
Двухконтурный автогенератор
|
|
|
|
Пусть с контуром L 1 C 1 R 1 автогенератора (рис. 67) индуктивно связан дополнительный колебательный контур L 2 C 2 R 2, например, резонансная нагрузка.
Рис. 67. Генератор с двумя степенями свободы с реактивной связью между контурами.
|
Уравнения для токов в первом и втором контурах имеют вид
Из рисунка видно, что
, 
.
Введём следующие обозначения
, 
, 
, 
, 
, 
.
Характеристику полевого транзистора можно аппроксимировать следующим выражением
 .
| (7.31) |
Введя все эти обозначения, получим уравнения колебаний напряжений в контурах:
Введём среднюю крутизну (колебательную характеристику) 
(см. пункт 6.2). Её введение позволяет перейти к следующим уравнениям:
Решение этой системы будем искать в виде, аналогичном (7.5)
, 
(фазовый сдвиг мы должны вводить, так как система диссипативна).
Будем в дальнейшем считать, что изменяющейся величиной является лишь парциальная частота n 1, а n 2 остаётся постоянной. Подставляем решение в систему, и вводя относительные расстройки относительно той частоты, для которой мы ищем решение
, 
,
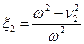получаем уравнения гармонического баланса
| (7.32) |
Здесь h 1,2 = 2 d 1,2/ w - декременты затухания первого и второго контуров соответственно.
Из последних двух уравнений системы (7.32) найдём отношение амплитуд колебаний в первом и втором контурах и сдвиг фаз между этими колебаниями:
, 
.
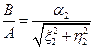Подставляя полученные выражения в первые два уравнения системы (7.32), имеем
 ,
| (7.33) |
 ,
| (7.34) |
где k 2 = a 1 a 2 - коэффициент связи между контурами.
Для определения средней крутизны подставим в (7.31) гармоническое решение, тогда
.
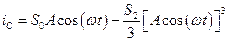Выписав выражение только для первой гармоники тока стока, и вспомнив определение средней крутизны, получим колебательную характеристику в виде
|
|
|
 ,
| (7.35) |
где IС 1 - амплитуда первой гармоники тока стока, A - амплитуда напряжения. Теперь подставляя (7.35) в (7.34), получим выражение для амплитуды стационарных колебаний:
 ,
| (7.36) |
где обозначено
, 
.
В наших обозначениях A 0 - это установившаяся амплитуда генератора в отсутствии второго контура. Увеличение связи с дополнительным контуром уменьшает установившуюся амплитуду колебаний. Из (7.36) следует, что включение в схему второго контура эквивалентно появлению дополнительного затухания, которое зависит от частоты генерации.
В частном случае при равенстве парциальных частот контуров (x 1 = 0) получается, что уравнение (7.33) выполняется только в случае, когда
.
Это уравнение имеет три корня:
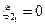и 
.
Последние два корня дают действительные значения x 2 только в том случае, когда k > h 2. Полученное неравенство указывает на существование критической связи между контурами kкр = h 2. При ненулевой расстройке и слабой k < k кр связи генерируемая частота w однозначно связана с парциальной частотой первого контура. Если k > kкр, то существуют три действительных корня уравнения. Проведём исследование этих двух случаев отдельно.
Рис. 68. Зависимость частоты генерируемого колебания от расстройки x 1 при слабой связи.
| Случай слабой связи между контурами (k < kкр). Зависимость x 2 от x 1 имеет вид, изображённый на рис. 68. Как уже было сказано, генерируемая частота однозначно связана с парциальной частотой первого контура. При этом если x 2 < 0 (n 2 > w), то эквивалентная парциальная частота понижается, т. е. дополнительный контур влияет как подключенная к основному контуру шунтирующая ёмкость. Если x 2 > 0 (n 2 < w), то добавка к парциальной частоте положительна, т. е. дополнительный контур эквивалентен подключению шунтирующей индуктивности. Амплитуду автоколебаний можно найти из соотношения (7.36). Наибольшее уменьшение амплитуды (отсос энергии из первого контура во второй) имеет место при равенстве парциальных частот (синхронизме), т. е. при x 1 = 0. Минимум амплитуды при этом: | |
 .
| (7.37) | |
Зависимость амплитуды автоколебаний от относительной расстройки изображена на рис. 69.
|
|
|
Рис. 69. Зависимость амплитуды генерируемого колебания от расстройки x 1 при слабой связи.
| 
Рис. 70. Зависимость амплитуды генерируемого колебания от расстройки x 1 вблизи области гашения.
|
Рис. 71. Зависимость частоты генерируемого колебания от расстройки x 1 при сильной связи.
| 
Рис. 72. Области отсоса энергии, гашения и затягивания колебаний.
|
Из (7.37) видно, что уменьшение амплитуды генерации при синхронизме тем больше, чем больше связь между контурами и меньше потери второго контура (больше добротность). При достаточно высокой добротности второго контура автоколебания в системе вблизи синхронизма контуров вообще могут быть подавлены, т. е. возможен режим с A = 0 (гашение колебаний). Условие такого гашения: k 2/ h 2 > MnS 0 - h 1. Зависимость амплитуды колебаний A от расстройки x 1 при наличии области гашения изображена на рис. 70 (область гашения заштрихована).
Случай сильной связи между контурами (k > kкр). В этом случае зависимость частоты генерации w от парциальной частоты первого контура n 1, т. е. x 2 от x 1 становится неоднозначной (имеет три ветви соответствующие трём корням уравнения (7.33)). Эта зависимость изображена на рис. 71. Исследование устойчивости колебаний показывает, что средняя ветвь частотной характеристики всегда неустойчива, т. е. генерируемая частота зависит от предыстории системы; генерация происходит либо на нижней ветви, либо на верхней. Это явление получило название затягивания. На рис. 72 показано расположение областей гашения, затягивания и отсоса энергии колебаний.
Затягивание колебаний
Затягивание колебаний обусловлено взаимодействием двух гармонических колебаний на активном нелинейном элементе (например, полевом транзисторе). Пусть вблизи равенства парциальных частот (рис. 71) в автогенераторе устойчивы колебания с нормальными частотами w 1 и w 2, следовательно, и их взвешенная сумма также будет устойчивым колебанием. Поэтому в режиме затягивания уже надо брать не гармоническое, а бигармоническое приближение. Таким образом, вблизи равенства парциальных частот нужно пользоваться бигармоническим балансом, тогда напряжение затвор-исток представим в виде
|
|
|
.
В рассматриваемом случае колебанию на каждой частоте соответствует своя средняя крутизна. Поэтому колебательная характеристика вычисляется на каждой частоте отдельно (в этом особенность бигармонического баланса). Тогда, подставляя выражение для напряжения в (7.31), найдём компоненты тока стока с частотами w 1 и w 2:
, 
.
Таким образом, колебательные характеристики на частотах w 1 и w 2:
 ,  .
| (7.38) |
Как видно, с ростом амплитуды обоих колебаний характеристики уменьшаются на каждой частоте. Но уменьшение колебательной характеристики на частоте w 1 в большей степени зависит от A 2, чем от A 1; уменьшение характеристики на частоте w 2 определяется в основном амплитудой A 1. Если подставить выражение (7.38) в уравнение (7.34), получим следующие выражения, связывающие амплитуды колебаний A 1 и A 2 с параметрами контуров:
| (7.39) |
где обозначено
, 
.
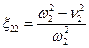Левые части уравнений (7.39) описывают вклад энергии в контуры, правые части - потери. Если при A 1 = A 2 = 0 подкачка энергии больше потерь (это соответствует мягкому режиму возбуждения), то развиваются оба колебания с нормальными частотами w 1 и w 2. Амплитуда их начинает расти, пока для одного из колебаний (для определённости, на частоте w 2) вклад не сравняется с потерями
, 
.
С этого момента амплитуда A 2 перестанет увеличиваться, а A 1 будет продолжать расти. Это приведёт к тому, что при расстройке x 22 накачка станет меньше потерь и A 2 начнёт уменьшаться, что увеличит скорость возрастания A 1. В итоге A 2 уменьшится до нуля, а A 1 возрастёт до такой величины, что будут выполняться соотношения
| (7.40) |
Первое из соотношений (7.40) - условие установления одномодовых колебаний на частоте w 1 с амплитудой A 1; неравенство показывает, что на частоте w 2 подкачка меньше потерь.
Аналогичным образом можно получить условия установления одномодового колебания с частотой w 2 и амплитудой A 2. Они имеют вид аналогичный (7.40)
|
|
|
, 
.
Простые соображения показывают, что гармонические колебания, описываемые соотношениями (7.40), устойчивы. Пусть, например, амплитуда A 1 немного возрастёт, тогда левая часть равенства (7.40) станет меньше правой и A 1 вновь уменьшится. Если A 1 уменьшится по сравнению со своим стационарным значением, то накачка на этой частоте станет больше потерь и A 1 вновь возрастёт. Вместе с тем небольшие изменения A 1 слабо сказываются на неравенстве (7.40) и накачка на частоте w 2 не сможет превысить потерь. Аналогичные рассуждения доказывают устойчивость колебаний, описываемых последними соотношениями.
Бигармонический режим, описываемый соотношениями (7.39), неустойчив. Действительно, при небольшом увеличении A 1 накачка на частоте w 2 уменьшается сильнее, чем накачка на частоте w 1; это приводит к быстрому уменьшению A 2, что увеличивает накачку на частоте w 1. Поэтому небольшое увеличение A 1 по сравнению со стационарным значением ведёт к резкому уменьшению A 2 и росту A 1. Система переходит к гармоническим колебаниям с частотой w 1. Наоборот, небольшое уменьшение A 1 по сравнению со стационарным значением переводит систему в режим гармонических колебаний с частотой w 2.
Рис. 73. Зависимость амплитуды генерируемого колебания от расстройки x 1 в режиме затягивания.
| Рассмотрим теперь поведение системы в зависимости от изменения парциальной частоты первого контура, т. е. относительно расстройки x 1. При частоте n 1 << n 2 (x 1 < 0) в системе существует гармоническое колебание с частотой w 1 близкой к n 1. При увеличении n 1 система входит в область, где возможно существование колебаний как частоты w 1, так и частоты w 2. Эта область носит название области затягивания частоты. В области затягивания режим генерации зависит от предыстории. Если система вошла в область со стороны x 1 < 0 (рис. 71 и 73), то в ней будут существовать колебания с частотой w 1 и амплитудой A 1. При |
дальнейшем увеличении x 1 система при x 1 = x 11 скачком перейдёт в режим генерации с частотой w 2 и амплитудой A 2. Если система входит в область затягивания со стороны x 1 > 0, то в ней происходят колебания с частотой w 2 и амплитудой A 2. Переход в режим с частотой w 1 и амплитудой A 1 наступает при x 1 = x 12. Расстройки x 11 и x 12, определяющие границы области затягивания, можно найти из условия нарушения устойчивости соответствующих колебаний.
|
|
|
