Общее уравнение динамики (принцип Даламбера-Лагранжа)

Метод кинетостатики (в некоторых источниках - принцип Даламбера-Лагранжа), обсужденный ранее в [8], позволяет обобщить принцип возможных перемещений на случай движения любой механической системы.

Рассмотрим несвободную механическую систему из материальных точек (), подчиненную идеальным связям. Согласно принципу Даламбера – Лагранжа, если к материальным точкам механической системы добавить их силы инерции, можно считать, что система сил уравновешена, то есть

; , (3.1)

где 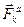- равнодействующая активных сил, приложенных к -ой точке системы, - равнодействующая реакций связей, а - сила инерции.

Определим из (3.1) равнодействующую реакций связей

. (3.2)

Сообщим точкам системы возможные перемещения , умножим обе части уравнения (3.2) на и просуммируем левые и правые части по индексу . Поскольку связи идеальные, то . (3.3) Тогда или . (3.4)

Уравнение (3.4), называемое общим уравнением динамики, является математической записью принципа Даламбера-Лагранжа: при движении механической системы, подчиненной идеальным связям, сумма работ активных сил и сил инерции на возможных перемещениях точек системы равна нулю. Название обусловлено тем, что из (3.4) можно вывести уравнения равновесия и общие теоремы механики.

В том случае, когда возможные перемещения точек механической системы можно выразить через независимые возможные перемещения (на механическую систему наложены геометрические связи), принцип Даламбера – Лагранжа может быть применен для каждого из этих перемещений. Очевидно, что в силу этой независимости количество выражений, аналогичных (3.4), будет равно числу степеней свободы механической системы.

Уравнение (3.4) справедливо и для систем с неидеальными связями. В этом случае следует формально включить силы реакций неидеальных связей в число задаваемых сил; эти силы должны быть рассчитаны предварительно каким-либо образом (например, используя уравнение равновесия, как это было сделано при решении примера 2.4, либо - общие теоремы механики, как это сделано ниже при решении примера 4.5; возможно и экспериментальное получение этих реакций).

ПРИМЕР 3.1. Составить дифференциальное уравнение движения первого груза механической системы из примера 2.3. Осевой момент инерции блоков полагать заданным.

РЕШЕНИЕ. На рис.3.1 изображена механическая система, внешние силы, на нее действующие, а так же силы и момент сил инерции.

Дадим системе возможное перемещение. Составим выражение суммы работ всех этих усилий на соответствующих возможных перемещениях и приравняем его к нулю. Тогда

где , , и -силы и момент сил инерции, приложенные к соответствующим телам, - сила вязкого сопротивления демпфера, - сила

упругости пружины.

Уравнения кинематических связей остаются прежними:

.

Тогда, в силу голономности и стационарности связей системы,

.

Вынесем за скобки, выражение в скобках приравняем к нулю. Соотношения между линейными ускорениями грузов и угловым ускорением блоков аналогичны приведенным выше (они получаются дифференцированием по времени уравнений кинематических связей). Выразим теперь кинематические характеристики в уравнении для суммы работ через скорость и ускорение первого груза. После несложных преобразований и учета условия статического равновесия (см. решение примера 2.3), получим дифференциальное уравнение колебаний системы около положения статического равновесия при наличии линейно-вязкого сопротивления:

.

Для получения решения уравнения необходимо задать начальные условия.

Замечания: - если есть необходимость получить дифференциальное уравнение движения другого тела системы следует воспользоваться уравнениями кинематических связей;

- алгоритм получения дифференциального уравнения не отличается от алгоритма получения уравнения равновесия; наличие сил, зависящих от кинематических характеристик, обуславливает различие структур этих уравнений;

- в случае движения системы с несколькими степенями свободы придется составить соответствующее число дифференциальных уравнений; в общем случае будет получена замкнутая система связанных дифференциальных уравнений второго порядка. Алгоритм получения каждого из уравнений остается прежним.