Каноническая форма задач линейного программирования

Общая и основная задачи линейного программирования

В предыдущем параграфе были рассмотрены примеры задач линейного программирования. Во всех этих задачах требовалось найти максимум или минимум линейной функции при условии, что ее переменные принимали неотрицательные значения и удовлетворяли некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этих задач является частным случаем общей задачи линейного программирования.

Определение 1.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

(8)

при условиях

(9)

(10)

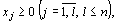(11)

где - заданные постоянные величины и .

Определение 2.

Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.

Определение 3.

Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.

Определение 4.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.

Определение 5.

Совокупность чисел ,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).

Определение 6.

План , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через 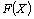. Следовательно, X^* – оптимальный план задачи, если для любого Х выполняется неравенство [соответственно ].

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции , можно перейти к нахождению максимума функции , поскольку .

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

преобразуется в ограничение-равенство

(12)

а ограничение-неравенство

– в ограничение-равенство

(13)

В то же время каждое уравнение системы ограничений

можно записать в виде неравенств:

(14)

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными и , приняв .

 

 

Каноническая форма задач линейного программирования

В каждой задаче ЛП ищутся значения переменных при условии, чтобы:

• эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
• при этих значениях целевая функция обращалась бы в минимум или максимум.

Одним из универсальных методов ЛП является симплексный метод, который, однако, можно применять, если задача ЛП имеет каноническую форму.

Определение. Задача ЛП имеет каноническую форму, если все ограничения системы состоят только из уравнений (кроме неравенств, выражающих неотрицательность переменных) и целевую функцию необходимо минимизировать.
Примером такой задачи ЛП в канонической форме является задача 1 – сбалансированная транспортная задача с системой ограничений (1) и целевой функцией (2).
Однако в большинстве экономических задач чаще всего в систему ограничений первоначально входят не только уравнения, а и неравенства.

Утверждение. Любая общая задача ЛП может быть приведена к канонической форме.
Приведение общей задачи ЛП к канонической форме достигается путем введения новых (их называют дополнительными) переменных.
Система ограничений (3) этой задачи состоит из четырех неравенств. Введя дополнительные переменные y ₁ ≥ 0, y ₂ ≥ 0, y ₃ ≥ 0, y ₄ ≥ 0, можно перейти к системе ограничений:

Эти дополнительные переменные y _i имеют абсолютно ясный экономический смысл, а именно означают величину неиспользованного времени работы (простоя машины i -го вида).
Например, если бы машины первого вида работали все 18 ч, то x + y = 18, следовательно, y ₁ = 0. Но мы допускаем возможность неполного использования времени работы первой машины x + y <18. В этом случае y ₁ приобретает положительное значение и может рассматриваться как неиспользованный лимит времени. Например, зная решение этой задачи из пункта 3.3.2, x = 12, y = 6, мы можем из системы ограничений (3.9) сделать вывод, что y ₁ = y ₂ = y ₃ = 0, а y ₄ = 12 – 6 = 6. Т. е. машины первого, второго, третьего вида используют свое рабочее время полностью. А вот четвертая машина загружена лишь наполовину, 6 часов, и при заданном оптимальном плане простаивает. Возможно, после таких выводов руководителю предприятия захочется загрузить ее другой работой, сдать в аренду на это время и т.д.
Итак, введением дополнительных переменных мы можем любое ограничение типа неравенства привести к уравнению.

Рассмотрим задачу о смеси. Система ограничений имеет вид:

Неравенства были обращены в сторону «больше», поэтому вводя дополнительные переменные y ₁, y ₂, y ₃ ≥ 0, их необходимо вычесть из левой части, чтобы уравнять ее с правой. Получим систему ограничений в канонической форме:

Переменные y_i также будут иметь экономический смысл. Если вы вспомните практическое содержание задачи, то переменная y ₁ будет означать количество излишнего вещества А в смеси, y ₂ –количество излишков вещества В в смеси, y ₃ – излишки С в смеси.
Задача нахождения максимального значения целевой функции может быть сведена к нахождению минимума для функции – F ввиду очевидности утверждения max F = –min (– F). Посмотрите на рисунок 3.9: если в какой-то точке x = x ₀ функция y = F (x) достигает своего максимума, то функция y = – F (x), симметричная ей относительно оси OX, в этой же точке x ₀ достигнет минимума, причем F _max = – (– F _min) при x = x ₀.

Вывод. Для представления задачи ЛП в канонической форме необходимо:

• неравенства, входящие в систему ограничений задачи, преобразовать в уравнения с помощью введения дополнительных переменных;
• если целевая функция F →max (максимизируется), она заменяется на функцию – F → min (которая минимизируется).

 

Поделиться:

Воспользуйтесь поиском по сайту: