 |
Простейшие действия с матрицами
|
|
|
|
Введение
Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «Электроэнергетика и электротехника» и профилю «электрооборудование и электрохозяйство предприятий, организаций и учреждений», в изучении линейной и векторной алгебры, аналитической геометрии, а также в выполнении контрольных работ по высшей математике по соответствующим темам: № 1, №2, №3.
В пособии содержатся три раздела, в каждом из которых имеется необходимый теоретический материал, пример выполнения соответствующей контрольной работы и задания для самостоятельного выполнения в десяти вариантах. Номер варианта определяется по последней цифре зачётной книжки (шифра).
Работу следует выполнять в тонкой ученической тетради в клетку. Выполненную работу следует снабдить титульным листом, образец которого можно найти на доске объявлений у деканата.
Поскольку пособие содержит достаточно большой теоретический материал, полезно сохранить его до конца обучения в вузе, так как он может быть востребован при дальнейшем изучении математики и других дисциплин.
Раздел 1. Контрольная работа по высшей математике №1
Теоретический материал по линейной алгебре
Комплексные числа и действия с ними
Под комплексным числом в алгебраической форме записи понимается выражение 
где 
и 
– действительные числа, а 
– мнимая единица, для которой справедлива формула 
Числа вида 
отождествляются с действительными числами, числа вида 
называются чисто мнимыми. Сопряженным числом 
к числу называется комплексное число 
Два комплексных числа 
и 
равны, если 
и 
Сложение, вычитание, умножение и деление комплексных чисел определяются следующим образом.
|
|
|
1) 
2) 
3) 
Примечание. Формулу умножения двух комплексных чисел не обязательно запоминать, так как она получается, если формально перемножить двучлены и по обычному правилу умножения двучленов и затем заменить 
на –1.
Примеры.
1. Найти сумму и произведение комплексных чисел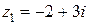 
и 
Находим сумму: 
Умножим: 
2. Найти частное комплексных чисел 
и 
Для нахождения частного умножим числитель и знаменатель дроби на число, сопряженное знаменателю:
|
Комплексное число 
можно изобразить точкой на плоскости 
имеющей координаты 
На оси 
изображаются действительные числа, поэтому она называется действительной осью; на оси 
расположены чисто мнимые числа; она называется мнимой осью.
Можно также сопоставить числу 
вектор, направленный из начала координат в точку 
Длина этого вектора 
, т.е. расстояние от начала координат до точки 
называется модулем комплексного числа 
и обозначается 
Из рисунка находим 
Следовательно:
Такая форма записи комплексного числа называется тригонометрической. Угол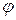 
, образованный радиус-вектором 
с положительным направлением действительной оси 
называется аргументом комплексного числа и обозначается 
. В инженерных приложениях угол 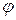также называется фазой. Величина угла 
определяется с точностью до слагаемого 
Главным называется значение , удовлетворяющее условию: 
.
Главное значение аргумента можно вычислить по следующим формулам:
Пусть 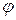– любое действительное число. Символом 
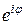обозначается комплексное число 
С помощью этого обозначения всякое комплексное число 
может быть записано в показательной форме (формула Эйлера):
Пример. Представить в тригонометрической и показательной форме комплексное число 
Находим модуль 
Аргумент находим по формуле:
.
Следовательно 
Матрицы и действия с ними
|
|
|
Матрица представляет собой прямоугольный массив чисел, образующих строки и столбцы одинаковой длины.
Для краткого обозначения матриц применяются латинские буквы A, B, C и т.д. Если в матрице m строк и n столбцов, то говорят, что матрица имеет размер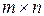 
. В общем виде элементы матрицы принято обозначать латинскими буквами a, b, c и т.д. Элемент, стоящий в i -той строке (т.е. в строке с номером i) и j -том столбце (т.е. столбце с номером j), обозначается 
и т.д. Учитывая введенные обозначения, произвольная матрица А может быть записана так:
.
Кроме больших круглых скобок, массив чисел, образующих матрицу может быть заключен в большие квадратные скобки или ограничен сдвоенными чертами. Многоточие в записи означает, что за элементом 
следуют элементы 
и т.д. до 
; за элементом 
следуют элементы 
и т.д. до элемента 
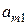. Элементами матрицы могут быть любые действительные и комплексные числа.
Если в матрице число строк и столбцов совпадает, т.е. 
, то матрица называется квадратной, а число 
указывает порядок матрицы.
Направление из левого верхнего в правый нижний угол квадратной матрицы называется главной диагональю, а элементы 
— диагональными элементами. Их сумма 
, кратко обозначаемая 
, называется следом матрицы 
. Направление, перпендикулярное главной диагонали, называется побочной диагональю.
Если в квадратной матрице все элементы, стоящие выше или ниже одной из диагоналей, равны 0, например,
то такие матрицы называются треугольными.
Если равны 0 все элементы, кроме стоящих на главной диагонали, то такая матрица называется диагональной:
.
Если все диагональные элементы равны 1, то такая матрица называется единичной:
.
Матрица, не обязательно квадратная, все элементы которой равны 0, называется нулевой.
Матрица, состоящая из одного столбца, называется матрицей-столбцом, матрица, состоящая из одной строки, называется матрицей-строкой.
Две матрицы называются равными, если они одного размера и все соответствующие элементы совпадают.
Под нормой матрицы А понимается действительное число 
, аналогичное понятию модуля для действительных чисел. Из элементов матрицы А ее норму можно составить различными способами, в дальнейшем за норму будем принимать корень квадратный из суммы квадратов всех элементов матрицы:
|
|
|
Простейшие действия с матрицами
1) Транспонирование.
Матрица 
называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
.
2) Сложение (вычитание) матриц.
Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц, например,
;
.
Замечание: исходя из определения, складывать или вычитать можно только матрицы одного размера.
3) Умножение на число (скаляр).
Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,
.
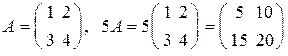Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.
Умножение матриц
Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:
.
Т.е. элемент матрицы С, стоящий в -той строке и 
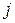-том столбце, равен сумме произведений соответствующих элементов -той строки матрицы А и 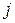-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера 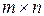на матрицу В размера 
дает матрицу С размера 
.
Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.
Пример.
.
.
Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 2, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:
;
;
.
Свойства умножения матриц
1) В общем случае 
, т.е. в общем случае перестановочное свойство умножения не выполняется.
Матрицы, для которых оно выполняется, называются перестановочными.
|
|
|
2) Сочетательное свойство: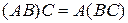 
.
3) Распределительное свойство умножения относительно сложения:
4) Умножение на единичную матрицу не меняет матрицы: 
.
5) Умножение на нулевую матрицу дает нулевую матрицу: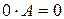 
;
замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что либо одна из них, либо обе вместе равны 0.
Матричные уравнения
Используя различные действия с матрицами, можно составлять матричные уравнения — соотношения между неизвестной матрицей Х и известными матрицами.
Например, АХ = В или ХА = В, АХВ = С, АХ + В = С, ХА — В = С и т.д.
Рассмотрим одно из простейших матричных уравнений:
.
В школьном курсе алгебры рассматривалось соответствующее ему уравнение для действительных чисел:
Решением этого линейного уравнения является 
, где число 
называется обратным к и удовлетворяет соотношению: 
.
Введем подобное понятие и для матриц. Матрица 
называется обратной к 
, если она удовлетворяет условию:
,
где 
— единичная матрица.
Из определения обратной матрицы следует, что ее можно найти только для квадратных матриц.
Существование обратной матрицы дает возможность решать матричные уравнения, например, рассмотрим уравнение . Умножим обе части уравнения слева на матрицу, обратную :
.
Аналогично можно найти решение уравнения 
, умножая теперь уже справа обе части уравнения на :
.
|
|
|
