 |
Дифференциальное исчисление функции нескольких переменных
|
|
|
|
При вычислении частной производной по одной переменной все остальные переменные считаются константами, поэтому техника дифференцирования функции нескольких переменных включает те же правила и приемы, которые используются при нахождении производных функций одной переменной.
Для функции z= f (x, y) полный дифференциал
. (54)
Если x и y – независимые переменные и функция f (x, y) имеет непрерывные частные производные, то
. (55)
Точки экстремума функции относительно некоторого множества называют точками относительного экстремума, или условного экстремума функции.
Задачу нахождения условного экстремума будем рассматривать для частного случая функции двух переменных 
, определенной на 
, при условии, что множество Е имеет вид:
,
где 
– некоторая функция, определенная на D. Уравнение 
называется в данной задаче уравнением связи.
Пример 4.2.1. <Дана функция 
. Найти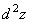 
.
Решение. Используя свойства (51), (52), (53), вычислим частные производные первого и второго порядка:
Ответ: 
►
Пример 4.2.2. Найти экстремум функции 
при условии 
.
Решение. Запишем уравнение связи в виде 
. style='color:black'>Найдем экстремум функции относительно множества 
.
Из уравнения связи выразим одну переменную через другую и получим функцию одной переменной
.
Функция 
зависит только от одной переменной, поэтому, вычисляя производную, определяем точки её экстремума
.
Так как вторая производная положительна, то имеем для функции строгий минимум. Подставляя найденное значение 
в уравнение связи, находим координаты точки условного минимума 
.
Таким образом, функция 
имеет строгий минимум относительно множества в точке 
, равный 
.
Ответ: 
. ►
Пример 4.2.3. Найти экстремум функции 
|
|
|
Решение. Область определения данной функции 
.Находим частные производные первого порядка
.
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки из системы уравнений
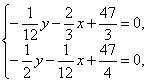или 
Решая данную систему, получаем 
, т.е. точка 
– стационарная точка.
Находим значения частных производных второго порядка в точке 
:
.
Тогда
,
следовательно, в точке функция имеет максимум: 
.
Ответ: 
►
Частные производные
2.1. Частные производные.
Множество точек М, которые удовлетворяют неравенству 
(М; М 
)< 
, называют -окрестностью точки М .
Пусть функция двух переменных z
=
f (x; у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x; у). Дадим переменной х приращение 
так, чтобы точка (х+ ; у) принадлежала этой окрестности. При этом функция z
=
f (x; у) изменится на величину
,
которая называется частичным приращением функции z
=
f (x; у) по переменной х.
Аналогично величину
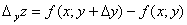
называют частичным приращением функции по переменной у.
Если существует предел
,
то его называют частной производной функции z
=
f (x; у) в точке М (x; у) по переменной х и обозначают такими символами:
, 
, 
, 
.
Аналогично
= 
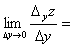
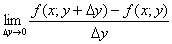
Из таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными.
Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей. Частные производные от частных производных , функции z
=
f (x; у) называются частными производными второго порядка. Функция двух переменных может иметь четыре частные производные второго порядка, которые обозначают так:
, 
,
, 
.
Производные 
и 
называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
|
|
|
Частные производные от частных производных второго порядка называются частными производными третьего порядка и т. д.
Само вычисление частной производной по существу не представляет ничего нового по сравнению с вычислением обыкновенной производной.
Пример 1: Найти частные производные функции
Решение:
(при дифференцировании по x мы считаем у=const, а при дифференцировании по у мы считаем x=const).
Пример 2: Найти частные производные функции
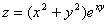
Решение: 
Пример 3: Пусть u= xу (x>0); частные производные этой функции будут: 
Первая из них вычисляется как производная степенной функции от х
(при у =const), а вторая - как производная показательной функции от у
(при х = const).
Пример 4: Если 
, то
Пример 5: Для 
имеем:
; 
; 
.
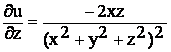Пример 6: Пусть 
, где 
- произвольная функция (имеющая производную).
Показать, что для z всегда выполняется соотношение:
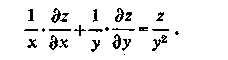
какова бы ни была функция 
.
По правилу дифференцирования сложной функции (означая штрихом производную по u) имеем:
и отсюда
Пример 7: Сторона a треугольника определяется по двум другим сторонам b
,
c и заключенному между ними углу a так: 
.
Тогда
. Геометрический смысл частных производных
Для большей геометрической наглядности и для того, чтобы не вводить новых понятий, в этом пункте ограничимся рассмотрением функций двух переменных.
Рассмотрим функцию z
= f
(
x
, у), определенную на плоском открытом множестве G
, т. е. множестве G
, лежащем на плоскости Е2.
Пусть (x
0
, у0) 
G
и пусть в точке (х0, у0) существует частная производная 
. Ее геометрический смысл сразу получается из определения частной
производной как обычной производной функции f
(
x
, у) по х при
фиксированном у и из геометрического смысла обычной производной.
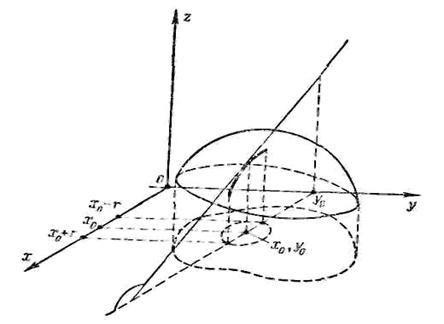
График 1 – геометрический смысл частных производных.
В самом деле, возьмем замкнутый круг Q
радиуса r
с центром в точке (x
0
, у0) и лежащий в G
*. Пусть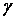 
- кривая, заданная представлением
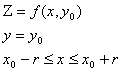
т. е. кривая, которая получается сечением графика функции z
=
f
(
x
, у), (х,
y
)
Q
плоскостью 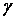= y
0.
* Такой круг Q
всегда существует. Действительно, в силу определения открытого множества существует такая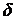 
-окрестность
O
точки (х0, у0), что О 
G
.
Тогда замкнутый круг
Q
радиуса 
с центром в точке (х0, у0) будет заведомо лежать в
G
.
|
|
|
Как известно,
где 
- угол, образованный касательной к графику функции f
(х,
у0) в точке (х0, f
(
x
0
,
у0)) с осью Ох, т. е. угол, образованный касательной к кривой 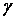в точке (x
0
, у0,
f
(х0,
у0)) с осью Ох.
Таким образом,
- в этом состоит геометрический смысл частной производной.
Совершенно аналогично устанавливается и геометрический смысл частной производной 
тангенса угла наклона, образованного касательной в точке (х0, f
(
x
0
,
у0)) к кривой, образованной сечением графика функции z=f(x, у), (х,y
)
Q
плоскостью х=х0, с осью Оу.
|
|
|
