 |
Формула Остроградского – Гаусса.
|
|
|
|
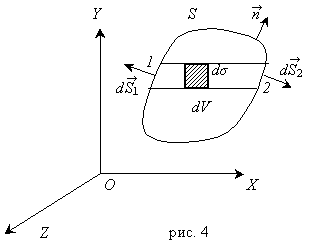
Пусть f (x, y, z) - некоторая функция, а S - замкнутая поверхность, ограничивающая объём V. На отрезке 1-2 (рис. 4), параллельном оси X, f - является функцией одного аргумента x. Интегрируя вдоль этого отрезка получим:
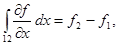
где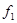 
и 
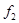- значения функции f на концах рассматриваемого промежутка.
Построим теперь бесконечно узкий цилиндр, одной из образующих которого является отрезок 1 2. Пусть dσ - площадь поперечного сечения его (величина положительная). Умножая предыдущее соотношение на dσ. Так как dσdx есть элементарный объём dV,заштрихованный на рисунке, то в результате получится:
,
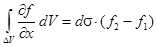где dV – часть объёма V, вырезаемого из него поверхность цилиндра. Пусть dS 1 и dS 2 эле -ментарные площадки, вырезаемые тем же цилиндром на поверхности S, а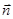 
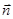1 и 2–
единичные нормали к ним, проведенные наружу от поверхности S. Тогда:
dσ = d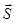 
2 
2х = - d 
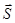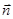1 1х,
а поэтому: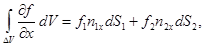 
или короче: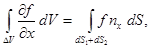 
где поверхностный интеграл распространён на сумму площадок dS 1 и dS 2. Весь объём V можно разделить на элементарные цилиндры рассматриваемого вида и написать для каждого из них такие же соотношения. Суммируя эти соотношения, получим:
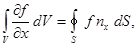(35)
Интеграл справа распространён по всему объёму V, справа – по поверхности S, ограничивающей этот объём. Аналогичные соотношения можно написать для осей Y и Z.
Возьмём теперь произвольный вектор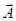 
и применим к его компонентам соотношение (35). Получим:
|
|
|
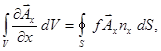
и аналогично для компонент A y и A z . Складывая эти соотношения, найдём:
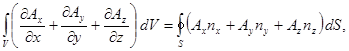
или:
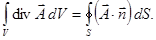
Эту формулу Остроградского – Гаусса можно также записать в виде:
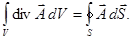
Смысл её заключается в том, что полный поток вектора 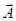через некоторую поверхность S равен суммарной алгебраической мощности источников, порождающих векторное поле.
Если объём V бесконечно мал, то величина div 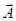внутри него может считаться постоянной. Вынося её за знак интеграла и переходя к пределу V → 0, получим:
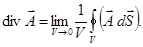
Предельный переход надо понимать в том смысле, что область V должна стягиваться в точку, т.е. размеры этой области должны беспредельно уменьшаться по всем направлениям. Эти рассуждения показывают, что величина, стоящая в правой части вышеуказанной формулы, не зависит от формы поверхности S, стягиваемой в точку. Поэтому это выражение можно принять за исходную формулировку дивергенции. Такое определение обладает преимуществом, потому что оно инвариантно, т.е. никак не связано с выбором координат.
Формула Стокса.
По определению ротор (вихрь) некоторого вектора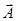 
:
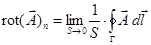(36)
Зная ротор вектора 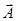в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру 
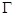, ограничивающему S, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы 
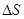. Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора 
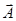по контуру, ограничивающему 
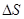, может быть представлена в виде.
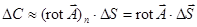(37)
|
|
|
где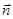 
- положительная нормаль к элементу поверхности .
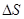Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем 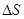, и тогда получим циркуляцию вектора 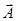по контуру 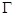, ограничивающему S:
.
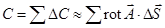Осуществив предельный переход, при котором все 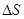стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:
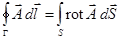(38)
Соотношение (38) носит название теоремы Стокса. Смысл её состоит в том, что циркуляция вектора 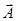по произвольному контуру 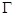равна потоку вектора 
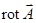через произвольную поверхность S, ограниченную данным контуром.
Список использованной литературы
1. Федорченко А. М. Классическая электродинамика. – К.: Вища школа, 1988. – 280 с.
2. Сивухин Д. В. Общий курс физики. Электричество. – М.: Наука, 1983. – 688 с.
3. Савельев И. В. Курс обшей физики. 3 том. – М.: Наука, 1988. – 496 с.
|
|
|
