Главная | Обратная связь | Поможем написать вашу работу!

Неравенство Клаузиуса. Закон возрастания энтропии

Равенство Клаузиуса. Энтропия

Рис. 13.1

Рассмотрим какую-либо термодинамическую систему и проведем с ней цикл Карно (рис. 13.1), состоящий из изотерм a-b и c-d и адиабат b-c и d-a. Согласно теореме Карно и определению термодинамической температуры, КПД цикла Карно, независимо от природы системы, равен

. (13.1)

Здесь Т ₁ и Т ₂ температуры на изотермах, Q_ab = Q ₁ – количество тепла, полученное системой от нагревателя на изотерме a-b, Q_cd = – Q ₂ – количество тепла, полученное системой от холодильника на изотерме c-d. Легко видеть, что соотношение (13.1) можно переписать в виде

. (13.2)

Отношение полученного системой количества тепла к температуре, при которой это тепло было получено, называют приведенным количеством теплоты. Как следует из соотношения (13.2) сумма приведенных количеств теплоты, полученных системой в цикле Карно, равна нулю.

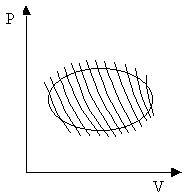Рис. 13.2

Покажем, что в любом обратимом цикле сумма приведенных количеств теплоты равна нулю. Чтобы цикл был обратимым, необходимо, чтобы на каждом его этапе температура рабочего тела бесконечно мало отличалась от температуры теплового резервуара (нагревателя или холодильника), с которым происходит теплообмен. Поэтому, вообще говоря, для проведения обратимого цикла требуется бесконечно большое число тепловых резервуаров.

Рассмотрим на P-V диаграмме произвольный обратимый цикл, изображенный на рис. 13.2. Проведем множество бесконечно близких адиабат, которые разобьют рассматриваемый цикл на «узкие» циклы, каждый из которых можно считать циклом Карно. К каждому такому циклу применим формулу (13.2). Сложив полученные выражения, придем к соотношению

. (13.3)

Это соотношение, являющееся следствием второго начала термодинамики, называется равенством Клаузиуса.

Рис. 13.3

Запишем равенство Клаузиуса для обратимого цикла 1-a-2-b-1 (рис. 13.3).

. (13.4)

Учитывая обратимость цикла, соотношение (13.4) можно переписать в виде

. (13.5)

Независимость интеграла (13.5) от пути перехода между состояниями 1 и 2 означает, что этот интеграл представляет собой изменение некоторой функции состояния системы, названной Клаузиусом энтропией S.

Энтропия - это функция состояния термодинамической системы, изменение которой в обратимом процессе равно приведенному количеству тепла. Энтропия в термодинамике определена с точностью до произвольной постоянной. В этом отношении с определением энтропии дело обстоит так же, как с определением потенциальной энергии в механике. Физический смысл имеет не сама энтропия, а лишь разности энтропий. Разность энтропий в состояниях 1 и 2 можно найти по формуле

, (13.6)

где интеграл вычисляется вдоль любого обратимого процесса, переводящего систему из 1 в 2.

В дифференциальной форме определение энтропии выглядит следующим образом:

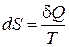. (13.7)

Используя соотношение (13.7), количество тепла, получаемое системой в бесконечно малом обратимом процессе, можно представить в виде

. (13.8)

Подставляя это выражение в первое начало термодинамики (3.3), получим

. (13.9)

Это уравнение называют основным термодинамическим тождеством. Оно объединяет первое и второе начала термодинамики. Применим соотношение (13.9) для вычисления изменения энтропии n молей идеального газа при переходе из состояния (T ₁, V ₁) в состояние (T ₂, V ₂).

Для идеального газа dU = n ×C_V×dT, P = n ×R×T/V. Подставляя dU и Р в (13.9) и деля на T, найдем

Интегрируя (при C_V = const), получим

. (13.10)

Процессы на T-S диаграмме

Формула (13.8) для элементарного количества тепла весьма похожа на формулу элементарной работы .

Ввиду этого сходства, Гиббс предложил называть энтропию S термодинамической координатой, а температуру Т – термодинамической силой. Так же, как работа связана с изменением механической координаты (объема), подвод тепла связан с изменением термодинамической координаты – энтропии.

a 2

1 b

S₁ S₂ S

Рис. 14.1

Геометрическая интерпретация количества тепла на диаграмме T-S совершенно аналогична интерпретации работы на диаграмме P-V. Полученное системой количество тепла выражается формулой

Геометрически оно равно площади фигуры, лежащей под кривой, изображающей процесс (рис. 14.1). Так как температура зависит не только от энтропии, а и от других параметров состояния (объема или давления), площадь под кривой (полученное тепло) зависит не только от начального и конечного состояний, но и от всего хода процесса (Q ₁_a₂ > Q ₁_b₂).

Рассмотрим цикл 1-а-2-b-1. На участке 1-а-2 энтропия растет, и система получает положительное количество тепла, равное площади фигуры 1-а-2-S₂-S₁-1. На участке 2-b-1 энтропия уменьшается, и система получает отрицательное количество тепла, абсолютная величина которого равна площади фигуры 2-b-1-S₁-S₂-1. Полное количество тепла Q, полученное системой при прохождении цикла, равно площади фигуры 1-а-2-b-1 (площади цикла). Так как внутренняя энергия U – функция состояния, ее изменение при обходе цикла равно нулю. Тогда из первого начала термодинамики следует, что Q = A, где А – полная работа, совершаемая системой за цикл. Таким образом, площади циклов на P-V плоскости и на T-S плоскости одинаковы.

Политропическим процессом (политропой) называют процесс, проходящей с постоянной теплоемкостью С. Найдем уравнение политропы в переменных T-S. Согласно определениям теплоемкости и энтропии, можно записать

Разделяя переменные, получим

Интегрируя, найдем уравнение политропы, проходящей через точку (S ₀ ,T ₀)

, .

Окончательно получим

. (14.1)

T C =0

C <0 C_V

C_P

T ₀ C = ¥

S ₀ S

Рис. 14.2

Таким образом, на T-S плоскости политропы с разными теплоемкостями образуют систему экспоненциальных кривых. На рис. 14.2 изображены изотерма (С = ¥), адиабата (С = 0), изохора (С = С_V), изобара (С = С_Р) и одна из политроп с отрицательной теплоемкостью (С < 0).

Подставляя в уравнение (14.1) выражение для изменения энтропии идеального газа можно получить уравнение политропы идеального газа в переменных T-V:

где n = (C – C_P) / (C – C_V) называется показателем политропы.

В переменных P-V уравнение политропы для идеального газа имеет вид:

Цикл Карно на T-S диаграмме всегда изображается прямоугольником, стороны которого параллельны координатным осям, тогда как на P-V диаграмме его форма зависит от вида рабочего вещества.

Докажем теорему: КПД цикла Карно больше, чем КПД любого обратимого цикла (отличного от цикла Карно), в котором максимальная температура равна температуре нагревателя, а минимальная – температуре холодильника в цикле Карно.

Для доказательства изобразим на T-S плоскости заданный цикл abcd и опишем вокруг него цикл Карно ABCD (рис. 14.3). КПД цикла Карно

где полученное от нагревателя количество тепла Q ₁ изображается на диаграмме площадью прямоугольника ABFE, а тепло Q ₂, отданное холодильнику, - площадью прямоугольника DCFE.

Обозначим сумму площадей фигур aAb и bBc через q ₁ (q ₁ > 0), а сумму площадей aDd и cCd через q ₂ (q ₂ > 0). Тогда КПД цикла abcd

Таким образом h_К > h. Теорема доказана.

Неравенство Клаузиуса. Закон возрастания энтропии

Напомним, что согласно второй теореме Карно (см. § 10), КПД h любой тепловой машины, проходящей цикл с использованием двух тепловых резервуаров, не может превышать КПД цикла Карно (h £ h_к). Обозначим температуры резервуаров Т_Н и Т_Х (Т_Н > Т_Х), а количества тепла, получаемые от них рабочим телом Q_Н и Q_Х соответственно (Q_Х < 0). Тогда h£ h_к, или

Отсюда следует, что

, (15.1)

т.е. сумма приведенных количеств теплоты в рассматриваемом цикле меньше или равна нулю. Соотношение (15.1) представляет собой частный случай неравенство Клаузиуса для цикла, в котором рабочее тело обменивается теплом с двумя тепловыми резервуарами.

Для произвольного цикла, в котором рабочее тело контактирует с большим числом тепловых резервуаров, неравенство Клаузиуса можно получить, разбивая цикл близкими друг к другу адиабатами на большое количество элементарных циклов, аналогично тому, как было получено равенство Клаузиуса в §13. Записывая для малых циклов соотношения (15.1) и суммируя, получим неравенство Клаузиуса, справедливое для любого цикла:

. (15.2)

Здесь Т – температура теплового резервуара, от которого рабочее тело получает элементарное количество теплоты d Q. Когда все процессы в цикле обратимы, при каждом элементарном акте теплопередачи температуры рабочего тела и резервуара неотличимы, и неравенство (15.2) переходит в равенство Клаузиуса (13.3).

Рассмотрим произвольный процесс 1-а-2 (обратимый или необратимый), переводящий систему из состояния 1 в состояние 2 (Рис. 15.1.). Вернемся в состояние 1, используя обратимый процесс 2-b-1. Запишем неравенство Клаузиуса для цикла 1-а-2-b-1:

. (15.3)

Для обратимого процесса 2-b- 1 приведенное количество теплоты равно изменению энтропии

Подставляя это выражение в неравенство (15.3), получим

. (15.4)

Таким образом, изменение энтропии в каком-либо процессе не может быть меньше приведенного количества теплоты. Неравенство (15.4) часто записывают в дифференциальной форме для бесконечно малых процессов

. (15.5)

Если процессы обратимы, выражения (15.4) и (15.5) переходят в равенства.

Для процессов, происходящих в теплоизолированной системе, d Q = 0. Тогда из неравенств (15.4) и (15.5) следует закон возрастания энтропии: энтропия адиабатически изолированной системы не может убывать. При обратимых процессах она остается неизменной, при необратимых процессах возрастает.

Чтобы найти изменение энтропии в необратимом процессе следует рассмотреть какой-либо обратимый процесс с теми же начальным и конечным состояниями, и рассчитать для него приведенное количество тепла.

В качестве примера найдем изменение энтропии идеального газа при расширении в пустоту от объема V ₁ до объема V ₂ в теплоизолированном сосуде. Так как в этом процессе газ работу не совершает и не получает тепла, его внутренняя энергия не меняется. Для идеального газа неизменность внутренней энергии означает постоянство температуры Т. Чтобы вычислить изменение энтропии газа рассмотрим квазистатический изотермический процесс, в котором газ находится в тепловом контакте с нагревателем, имеющим температуру Т. Медленно уменьшая давление на газ можно увеличить его объем от V ₁ до V ₂. При этом газ получит от нагревателя количество тепла Q, за счет которого совершит работу А.

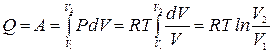Отсюда

Такое же возрастание энтропии будет при расширении в пустоту, хотя газ тепла не и получает. Увеличение энтропии вызвано необратимостью процесса.

Воспользуйтесь поиском по сайту: