 |
Некоторые примеры применения метода термодинамических функций
|
|
|
|
Термодинамические функции
С помощью энтропии можно получить много важных термодинамических соотношений и ввести в рассмотрение ряд новых полезных термодинамических функций.
Согласно первому началу термодинамики, изменение внутренней энергии в бесконечно малом процессе равно 
. Если процесс обратимый, то d Q = TdS.
Тогда выражение для бесконечно малого приращения внутренней энергии примет вид, характерный для полного дифференциала функции двух переменных - энтропии S и объема V:
. (16.1)
Если рассматривать внутреннюю энергию как функцию энтропии и объема
U = U (S,V), (16.2)
то ее дифференциал
. (16.3)
Сравнение соотношений (16.1) и (16.3) дает
, 
. (16.4)
Как отмечалось ранее (см. § 5), для полной характеристики термодинамических свойств системы надо знать термическое уравнение состояния f (P,V,T) = 0, связывающее температуру, давление и объем,и калорическое уравнение состояния, которое определяет зависимость внутренней энергии от каких-либо двух параметров состояния, например U = U (T,V). Однако, если независимыми переменными для внутренней энергии являются S и V, то температуру Т и давление Р можно найти с помощью соотношений (16.4), и необходимость в термическом уравнении состояния отпадает. По этой причине внутреннюю энергию U в переменных S и V (соотношение (16.2)) называют характеристической функцией. Производные от U (S,V) по характеристическим переменным выражают все термодинамические свойства системы.
Из математического анализа известно, что вторые смешанные частные производные функции двух переменных не зависят от порядка дифференцирования, поэтому 
.
Тогда из соотношений (16.4) следует, что
. (16.5)
Такие выражения в термодинамике называют соотношениями взаимности, или соотношениями Максвелла. Они широко используются для установления связей между термодинамическими величинами. Для получения подобных соотношений помимо внутренней энергии U могут быть использованы другие термодинамические функции, такие как энтальпия H, свободная энергия F, термодинамический потенциал G. Эти функции при надлежащем выборе независимых переменных так же являются характеристическими, т.е. позволяющими находить все термодинамические характеристики системы. Определения этих функций, их характеристические переменные, дифференциалы, производные и соотношения Максвелла приведены в таблице 16.1.
|
|
|
| Внутренняя энергия | Энтальпия | Свободная энергия Гельмгольца | Термодинамический потенциал Гиббса |
| U U = U (S,V) | H = U + PV H = H (S,P) | F = U – TS F = F (T,V) | G = U + PV – TS G = G (T,P) |
| dU = TdS – PdV | dH = TdS + VdP | dF = - SdT – PdV | dG = - SdT + VdP |
| 
| 
| 
|
|
(16.5)
| 
(16.6)
| 
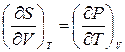(16.7)
| 
(16.8)
|
Функции U, H, F, G, имеющие размерность энергии, часто называют термодинамическими потенциалами. Термин «потенциал» указывает на аналогию этих функций с потенциальной энергией, дифференцирование которой по координатам дает значения соответствующих компонент силы. Изменения некоторых термодинамических потенциалов можно связать с обменом энергией между системой и окружающей средой:
изменение внутренней энергии U равно работе, совершенной над системой в адиабатическом процессе, или теплоте, полученной системой в изохорическом процессе;
изменение энтальпии Н равно теплоте, полученной системой в изобарическом процессе;
изменение свободной энергии F равно работе, совершенной над системой в изотермическом процессе.
Пользуясь таблицей 16.1 можно установить связь между термодинамическими функциями:
, 
Þ 
; (16.9)
, 
Þ 
. (16.10)
Соотношения (16.9) и (16.10) называются уравнениями Гиббса-Гельмгольца.
Некоторые примеры применения метода термодинамических функций
|
|
|
Пример 1. Исследуем зависимость внутренней энергии от объема. Для этого найдем производную (¶ U/ ¶ V) T. Изменение внутренней энергии в бесконечно малом обратимом процессе дается выражением (16.1)
dU = TdS –PdV.
Записав это равенство для изотермического процесса и поделив на dV, получим
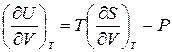. (17.1)
Учитывая соотношение Максвелла (16.7) 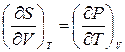, найдем
. (17.2)
Для идеального газа P = RT/V, (¶ P/ ¶ T) V = R/V, следовательно
и 
.
Значит, внутренняя энергия идеального газа не зависит от объема, а является функцией только температуры. Это закон Джоуля, который ранее уже использовался нами как эмпирический факт. Теперь мы видим, что он является следствием уравнения Клапейрона-Менделеева и второго начала термодинамики.
Напомним, что 
. Пользуясь независимостью вторых смешанных частных производных от порядка дифференцирования, получим
.
Отсюда следует, что теплоемкость CV идеального газа не зависит от объема, но может зависеть от температуры.
Пример 2. Совершенно аналогично можно найти производную (¶ H/ ¶ P) T.
,
, Þ
. (17.3)
Для идеального газа 
, 
. Таким образом, энтальпия идеального газа и его теплоемкость СР зависят только от температуры.
Пример 3. Разностьтеплоемкостей CP – CV.
В § 4 на основании первого начала термодинамики была получена формула
. (17.4)
Для вычисления CP – CV по этой формуле необходимо знать и термическое и калорическое уравнения состояния. Второе начало термодинамики и основанный на нем метод термодинамических функций дают возможность решить ту же задачу без использования калорического уравнения состояния. С помощью соотношения (17.2) можно исключить из формулы (17.4) производную (¶ U/ ¶ V) T. Это дает
. (17.5)
С помощью тождества (2.4)
формулу (17.5) можно преобразовать к виду
. (17.6)
Зная термическое уравнение состояния, можно по любой из этих формул найти CP – CV. В частности, для идеального газа PV = RT. В этом случае формулы (17.5) и (17.6) приводят к соотношению Майера CP – CV = R.
Если ввести в рассмотрение температурный коэффициент объемного расширения 
и изотермический модуль объемной упругости 
, то первую из формул (17.6) можно переписать в виде
. (17.7)
Так как КТ всегда больше нуля, из этого равенства следует, что для всех веществ CP > CV.
|
|
|
|
|
|
