 |
Апериодическое (инерционное) звено или звено 1-го порядка.
|
|
|
|
Звено, которое описывается уравнением вида:
где t - коэффициент передачи (усиления),

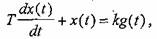
Т - постоянная времени, характеризующая инерционность (с), называется апериодическим звеном.
2. Переходя к преобразованию Лапласа

| (1) |
получим по определению передаточную функцию

| (2) |
3.1 Переходная характеристика такого звена при  представляет собой экспоненту
представляет собой экспоненту
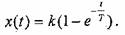
Переходный процесс достигает своего установившегося значения 0,95% практически за ЗГ (рис 12).

3.2 Импульсная переходная функция при  находится дифференцированием
находится дифференцированием 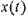 при
при  =1, получим
=1, получим


Если эти характеристики получены экспериментально, то по ним МОЖНО определить Ги &, как показано на рис. 33 и 34. и, таким образом, получить уравнение звена (что очень важно).
3.3.1 Частотная характеристика:
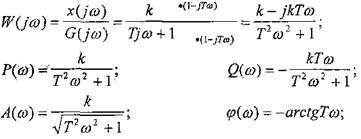
График ЧХ в обычном масштабе (рис.35).

3.3% ЛАХ: 
При k=1 
Построение:
- При малых частотах, где
 , пренебрегаем
, пренебрегаем  - 0.
- 0.

- При больших частотах, где
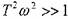 , пренебрегаем 1, тогда
, пренебрегаем 1, тогда

В области средних частот  , отсюда определяем частоту сопряжения низкочастотной и высокочастотном составляющей:
, отсюда определяем частоту сопряжения низкочастотной и высокочастотном составляющей: 
 Определим наклон высокочастотное составляющей, для чего вычислим изменение
Определим наклон высокочастотное составляющей, для чего вычислим изменение  при изменении частоты в 10 раз. т.е. при изменении частоты на одну декаду (в 10 раз),
при изменении частоты в 10 раз. т.е. при изменении частоты на одну декаду (в 10 раз),

ЛАХ уменьшается на 20 дБ, следовательно, наклон высокочастотной составляющей равен -20 дБ/дек.
Это мы построили приближенную характеристику. Действительная АЧХ отличается в частоте сопряжения, как известно из практики на 3 дБ (что допустимо для инженерных расчетов) (рис.15).
ЛФХ (рис.15):  -тангенсоида, при
-тангенсоида, при 
при 
при 
При  ЛАХ перемещается параллельно самой себе по оси ординат на величину
ЛАХ перемещается параллельно самой себе по оси ординат на величину  , ЛФХ - остается той же самой (рис.15).
, ЛФХ - остается той же самой (рис.15).
Лекция №6
Структурные преобразования
|
|
|
В результате разбиения САУ на типовые звенья направленного действия и получения их передаточных функций,
составляется структурная схема всей системы.
- Структурная схема - это диаграмма прохождения сигналов управления и их преобразования в САУ.
- Структурная схема - это математическая модель системы.
Структурные схемы для реальных САУ имеют сложный и запутанный вид. С целью упрощения
структурной схемы или приведения ее к более удобному виду, можно производить структурные преобразования по определенным правилам:


| (1) |
Правила преобрзвания структурных схем Преобразование последовательного соединенных звеньев.
Решая(1) совместно, получим  или передаточная функция двух последовательно соединенных звеньев
или передаточная функция двух последовательно соединенных звеньев
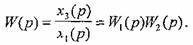
| (2) |
Итак, при n последовательно соединённых звеньев с передаточными функциями 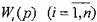
результирующая передаточная функция равна произведению передаточных функций отдельных звеньев:

2. Прсобрачованне параллельного соединенных звеньев.
- 
Решая (1) совместно, получим  или
или

Таким образом, перздаточная функция n параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев:

3. Звено, охваченное обратной связью:
3.1. ООС.

Решая (1) относительно  и
и 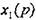 , получим:
, получим:

3.2. ПОС. Проводя аналогичные рассуждения, получим:

3.3. Частный случай: при единичной ОС.
Причём знак "+" соответствует
ООС.

Знак  "-" соответствует ПОС.
"-" соответствует ПОС.
Пример:

обозначив  и
и  ,получим
,получим  ;
;
Таким образом, интегрирующее звено, охваченное безынерционной обратной связью, эквивалента типовому апериодическому звену, т.е. уже не является интегрирующим.
Правила переноса сигнала
В общем случае структурные схемы могут иметь различного рода перекрещивающиеся связи поэтому для приведения структуры к одноконтурной - удобной для исследования, разработаны правил; переноса сигналов из одной точки структуры в другую:
1. При прямом переносе сигнала через ПФ W1:

2. При обратном переносе сигнала через ПФ W1:
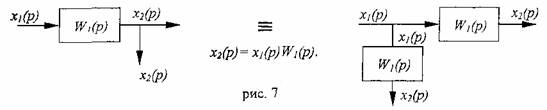
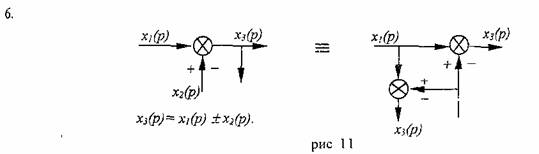
3. При прямом переносе суммирующего звена:

4. При обратном переносе суммирующего звена:

|
|
|
Замечание:
- Структурные преобразования можно производить только в том случае, если анализ динамической системы производится при нулевых начальных условиях. В противном случае структурные преобразования приводят к потере начальных условий и погрешностям при дальнейшем анализе.
- Структурные преобразования лишены физического смысла.
Лекция №7
Устойчивость - это основное качественное свойство системы автоматического управления, без которого она неработоспособна. Физически устойчивость означает, что процессы в системе стремятся к определенной величине при любых начальных условиях. На рис. 1. приведены переходные характеристики неустойчивой и устойчивой системы. Для последней справедливо условие

|
| Рис. 1. Переходные характеристики системы |

1 - сходящийся процесс, система устойчива.
2 - расходящийся процесс, система неустойчива.
Об устойчивости можно судить также по импульсным переходным функциям (рис. 2), которые для устойчивой системы удовлетворяют условию

В случае линейных САУ устойчивость определяется только ее структурой и параметрами и не зависит от внешних воздействий. Рассмотрим, как оценить это свойство для систем типа:

|
| Рис. 2. Импульсная переходная функция |

| (1) |
Переходные процессы в ней определяются как решение матричного уравнения состояния следующим образом:

| (2) |
Здесь первое слагаемое соответствует свободной составляющей движения, второе - вынужденной.
Основным режимом работы системы является равновесный (статический) режим, при котором переменные состояния с течением времени не меняются, а все производные координат состояния равны нулю.
Покажем, что процgесс движения к равновесию можно считать свободным. Предварительно запишем уравнение равновесия, полагая в (1) 

| (3) |
откуда при det  A определим равновесное значение переменных состояния
A определим равновесное значение переменных состояния

| (4) |
Введем новые координаты, равные отклонениям от точки равновесия,

| (5) |
и запишем уравнение в отклонениях:
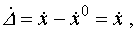 так как так как 
| (6) |
После подстановки в (6) вместо  его значения из (1) с учетом (5) получим
его значения из (1) с учетом (5) получим
|
|
|

Окончательно уравнение в отклонениях имеет вид:

| (7) |
Определение. Линейная система называется устойчивой, если для ее процессов выполняется свойство:

| (8) |
Вид процессов системы (7) определяется ее решением, которое находится через матричную экспоненту в виде

| (9) |
Поскольку выражение (9) соответствует первой составляющей решения (2), то устойчивость линейной системы (1) определяется только свойствами автономной системы и не зависит от внешних воздействий. Это означает, что можно не переходить к уравнениям в отклонениях от состояния равновесия, а для анализа устойчивости исследовать свойства матрицы A.
Лекция №8
Устойчивость (продолжение).
(Алгебраические критерии устойчивости.)

W = ∑ простые звенья.
 , где
, где  ,
, 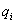 - корень полинома знаменателя передаточной функции W.
- корень полинома знаменателя передаточной функции W.
Пример:
 ,
,  . При
. При  , устойчивая система.
, устойчивая система.
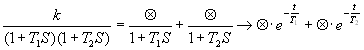 .
.
Если  - положительные числа, то система устойчивая.
- положительные числа, то система устойчивая.
Пример:
 система неустойчивая. Т.к.
система неустойчивая. Т.к.  - положительное числа, а
- положительное числа, а  - отрицательное.
- отрицательное. 

Т.к. не все корни знаменателя находятся в левой полуплоскости плоскости С, то система неустойчивая (есть одна растущая экспонента).
Определение: Корни знаменателя W называются полюсами.
Корни числителя W называются нулями.
Комментарий:
 ноль:
ноль:  , полюса:
, полюса:  .
.
 x – полюс.
x – полюс.
о – ноль.
Система устойчивая.
Правило: Для того, чтобы система была устойчивой необходимо и достаточно, чтобы все полюса системы находились в открытой левой полуплоскости С.
Для анализа, синтеза необходимо уметь отвечать на вопрос: “ Лежат ли все корни в левой полуплоскости плоскости С?” по коэффициентам полинома, не вычисляя корни:
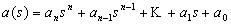 .
.
Определение: Правила, позволяющее получить ответ на вопрос об устойчивости системы без вычисления корней называются критериями устойчивости.
Имеются 2 группы критериев: алгебраические и частотные. Алгебраические: критерии Роуса и Гурвица.
|
|
|


