Прямоугольная система координат

ВВЕДЕНИЕ

 

Курс ’Начертательная геометрия. Инженерная и компьютерная графика’ входит в число дисциплин, составляющих основу инженерного образования.

Предметом начертательной геометрии является изложение и обоснование способов построения плоской модели трехмерного пространства и способов решения задач геометрического характера на базе этой модели. Однако, методы построения и преобразования чертежа преимущественно основаны на словесном описании и запоминании стандартных положений.

Такая трактовка трехмерного пространства не имеет явного сходства с положениями алгебры и тригонометрии, которые предлагают свою математическую модель трехмерного пространства.

Следовательно, начертательная геометрия в классической форме не предполагает использование ЭВМ, т.к. вычислительная техника воспринимает цифровую информацию с последующей математической обработкой ее в графическую. На базе графоматематической модели работают системы автоматизированного (с участием оператора) и автоматического управления объектами.

Одним из условий овладения техническими знаниями является умение читать (выполнять) конструкторские документы с учетом требований ЕСКД (единая система конструкторской документации) и СПДС (система проектной документации для строительства) и использовать при этом ЭВМ в режиме пользователя.

 

ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ

 

В данной работе рассматривается один из вариантов геометрической модели трехмерного пространства, позволяющей использовать понятия начертательной геометрии на ЭВМ.

Аппарат геометрической модели предполагает измерение длин в метрах и плоских углов в градусах или радианах.

Под длиной подразумевается расстояние между двумя точками. Измерение длины ведется вдоль некоторой прямой от заранее выбранной на ней точки - текущей базы БТ (БТ - точка, координаты которой внутри объекта равны нулю) (рис.1).

Рис. 1. Прямая a. БТ - текущая база; a - обозначенное направление; L - положительное расстояние до точки С; (-В) - отрицательное расстояние до точки D.

 

Линия на чертеже обозначается строчной буквой латинского алфавита.

 

Если измерение длины ведется в обозначенную сторону прямой, то длина считается положительной и наоборот.

Таким образом, прямая имеет положительное или отрицательное линейное направление.

Кроме того, она имеет угловое направление. Измерение угла принято вести от тригонометрического нуля.

Тригонометрический ноль – луч 0 с началом в БТ и направлен горизонтально вправо (рис.2).

Измеряется угол до положительного направления прямой. Если измерение угла против часовой стрелки, то угол положительный, по часовой - отрицательный.

Обозначается угол строчной буквой греческого алфавита.

Рис.2. Прямая a; j - положительный угол; (-j) - отрицательный угол; БТ – текущая база; 0 – тригонометрический ноль.

 

Математическая модель той же прямой Y=K ´ X + Y^БТ (изменение координаты Y точки прямой с изменением координаты Х; K = tg j).

 

Прямоугольная система координат

 

Приняв прямую за единственный элемент для моделирования трехмерного пространства, можно тремя пересекающимися в одной точке и не лежащими в одной плоскости прямыми образовать трехмерное пространство, обеспечивая измерение в трех направлениях.

В прямоугольной системе координат три прямые X, Yи Z взаимно перпендикулярны и пересекаются в одной точке, которая совпадает с началом координат 0 (рис. 3).

 

Для работы в системе необходим аппарат, который позволял бы определять и изменять положение объекта в этом пространстве, т.е. измерять и изменять расстояния и углы.

Если принять точку БТ(X, Y, Z) за базу параллелепипеда, то положение его в пространстве можно определить расстояниями от базы БТ до плоскостей П₁, П₂, П₃ и углами наклона граней к тем же плоскостям. БТ(X, Y, Z) – математическое уравнение точки.

 

Рис. 3

Если построить проекции БТ на плоскости плоскостей П₁, П₂, П₃ соответственно БТ₁, БТ₂ и БТ₃ и соединить проекции линиями связи (линия связи – ломаная линия, которая соединяет 2 проекции точки и перпендикулярна соответствующей оси), то:

 

координата X равна

расстоянию от БТ до П₃ или

расстоянию от БТ до проекции БТ₃ на П₃ или

расстоянию от БТ₂ до оси Z по линии связи к оси Z или

расстоянию от БТ₁ до оси Y по линии связи к оси Y или

расстоянию от 0 до линии связи к оси Х;

 

координата Y равна

расстоянию от БТ до П₂ или

расстоянию от БТ до проекции БТ₂ на П₂ или

расстоянию от БТ₁ до оси X по линии связи к оси X или

расстоянию от БТ₃ до оси Z по линии связи к оси Z или

расстоянию от 0 до линии связи к оси Y;

 

координата Z равна

расстоянию от БТ до П₁ или

расстоянию от БТ до проекции БТ₁ на П₁ или

расстоянию от БТ₂ до оси X по линии связи к оси X или

расстоянию от БТ₃ до оси Y по линии связи к оси Y или

расстоянию от 0 до линии связи к оси Z.

 

 

Прямые X^A, Y^A и Z^A образуют внутреннюю прямоугольную систему координат объекта с базой в точке БТ. Если менять координаты БТ, то изменится положение объекта в пространстве (изменятся расстояния до плоскостей проекций).

На рис. 3 уменьшена координата Х базы параллелепипеда. В результате параллелепипед из исходного положения вместе с внутренней системой координат переместился вправо в 1 текущее положение (текущая база БТ¹).

Объект можно вращать вокруг его внутренних осей координат. j^Х – направление вращения вокруг оси Х^А, j^Y - направление вращения вокруг оси Y^А, j^Z - направление вращения вокруг оси Z^А. При этом будут меняться углы наклона граней объекта к П₁, П₂, П₃.

На рис.3 в 1 текущем положении параллелепипед повернут вокруг оси Y^A1 на угол a. На тот же угол изменилось направление осей X^A1, Z^A1 и углы наклона граней к плоскостям П₁ и П₃. При этом на плоскостях П₁ и П₃ изменились геометрические размеры проекций, т.к. длина проекции прямой на плоскость П₁

А₁В₁ = АВ ´ Cos a, (1)

длина проекции прямой на плоскость П₃

А₃В₃ = АВ ´ Cos g. (2)

Угол наклона к П₂ не изменился, т.к. ось вращения Y^A1 перпендикулярна данной плоскости проекций. Не изменяются и геометрические размеры проекции на плоскости П₂, т. к. длины проекций прямых

А₂В₂ = АВ ´ Cos b. (3)

 

Длина проекции отрезка прямой на плоскость изменяется от 0 до натуральной величины отрезка (предел изменения Cos угла от 0 до 1).

a - угол наклона к горизонтальной плоскости.

b - угол наклона к фронтальной плоскости.

g - угол наклона к профильной плоскости.

 

Следовательно, по проекциям объекта можно определить место его в пространстве и углы наклона к плоскостям проекций, а так же взаимное положение объектов.

Изображение объекта на плоскость - проекция объекта, обозначается именем объекта с индексом плоскости, на которой он изображен. БТ₁(X, Y, 0) - горизонтальная проекция точки БТ, БТ₂(X, 0, Z) - фронтальная, БТ₃(0, Y, Z) - профильная.

На основании изложенного, возможна плоская модель трехмерного пространства, которая заменит при измерении длин и углов объемную модель.

 

Для формирования плоской модели введем определения:

 

- точка A - пересечение двух линий, обозначается

прописной буквой латинского алфавита; (4)

Математическое уравнение точки А(X, Y, Z). X, Y, Z – цифры, которые не имеют физического смыла, следовательно, их можно получить при решении системы двух уравнений, каждое из них имеет физический смысл, например, линий Y=f(X) и Z=f(X).

 

- плоскость Σ - две пересекающиеся прямые, обозначается

прописной буквой греческого алфавита; (5)

 

- отрезок (AB) – участок прямой между двумя точками. (6)

 

В соответствии с определением (5):

 

- прямые X и Y образуют горизонтальную плоскость П₁ (рис. 4а), на ней изображаются только горизонтальные проекции, например, БТ₁(X, Y);

- прямые X и Z образуют фронтальную плоскость П₂ (рис. 4б), на ней изображаются только фронтальные проекции, например, БТ₂(X, Z);

- прямые Y и Z образуют профильную плоскость П₃ (рис. 4в), на ней изображаются только профильные проекции, например, БТ₃(Y, Z).

Плоскости П₁, П₂, П₃ называются основными плоскостями проекций, т.е. на них будем изображать расположенный в пространстве объект, например, точку БТ. При этом объект находится между наблюдателем и плоскостью проекций.

Рис. 4

 

Чтобы получить проекцию точки, достаточно из нее опустить перпендикуляр на плоскость. Точка пересечения перпендикуляра с плоскостью - проекция точки на соответствующую плоскость.

 

Если три изображения рис. 4 совместить (наложить одно на другое), то получим плоскую модель прямоугольной системы координат (рис. 5).

 

 

Рис. 5

 

Оси X, Y и Z для различных плоскостей проекций совпадают, но отличаются линейным или угловым направлением.

 

Оси X1 (уравнение Y=0) и X2 (уравнение Z=0) совпадают, ось Y3 (уравнение X=0) совпадает с ними, но имеет противоположное направление.

Оси Z2 (уравнение X=0) и Z3 (уравнение X=0) совпадают, ось Y1 (уравнение X=0) совпадает с ними, но имеет противоположное направление.

Дуга t означает, что расстояние Y, отложенное по оси Y1 с некоторой степенью точности, перенесено на ось Y3 c той же погрешностью. Дуга t не принадлежит линии связи и ее можно заменить прямой под углом 45°. В обеих случаях точка пересечения l _y1 с осью y ₁ будет перенесена на ось y ₃, через эту точку пройдет линия связиl _y3 к оси y ₃.

 

Пример: Построить точку В(-20, -15, 25).

Построить точку - значит построить ее проекции в прямоугольной системе координат В(В₁, В₂, В₃).

Если горизонтальная и фронтальная проекции имеют одинаковую координату х, то они лежат на одной линии связи к оси x (рис. 6). Для построения ее отложим по оси x координату X = -20 и проведем l_X (X = -20 - математическое уравнение прямой l_X.

 

По линии связи l_X отложим от оси Х координату Z = 25, получим фронтальную проекцию В₂. На той же линии связи отложим Y = -15, получим горизонтальную проекцию В₁.

Профильную проекцию В₃

следует получить на пересечении линий связи к осям z и y l _Z и l _y3.

Если заданы проекции точки, то положение ее в реальном пространстве, например, в комнате, где расположен наблюдатель, можно описать следующим образом:

- поскольку координата X отрицательная, то точка находится за боковой стеной;

- поскольку координата Y отрицательная, то точка находится за фронтальной стеной;

- поскольку Z положительная, то точка находится над полом.

Рис. 6

 

Положение объекта в пространстве определено, если есть проекции его на 2 плоскости, например, П₁ и П₂ (рис. 7), т.е. известны координаты X = ½0 l _X ½, Y = ½C₁ x ₁₂½, Z = ½C₂ x ₁₂½.

 

Рис. 7

 

Домашняя работа выполняются к очередному практическому

занятию.

Выполняются домашние и аудиторные работы на чертежной бумаге формата А4 (страница 51, литература [1]). На первом листе выполняется основная надпись типа рис.42, на остальных типа рис.44. (страница 52, литература [1]). При наличии методических указаний задачи можно выполнять непосредственно в них.

 

Задания:

1. Построить фронтальные проекции параллелепипеда в исходном и первом положениях (рис. 3). Построить профильную проекцию параллелепипеда в первом положении.

2. Обозначить оси. Построить недостающие проекции точек А, В, С (Рис. 8).

Рис. 8

Прямая линия

 

Прямая в прямоугольной системе координат задается положением ее текущей базы, например, точкой A(X, Y, Z) и углами наклона к плоскостям проекций a к П₁, b к П₂, g к П₃ (рис. 9).

 

 

Угол наклона прямой к плоскости измеряется между (7)

самой прямой и ее проекцией на эту плоскость

 

Под самой прямой на плоской модели будем подразумевать проекцию, длина которой равна модулю.

На основании (4): угол a = (MN)^(M₁N₁);

угол b = (MN)^(N₂M₂);

угол g = (MN)^(M₃N₃).

На рис. 9 прямая задана отрезком АВ. Построены проекции отрезка А₁В₁- горизонтальная, А₂В₂ – фронтальная и А₃В₃ – профильная. Если прямая бесконечна, то она пересекает горизонтальную плоскость П₁ в точке М, фронтальную плоскость П₂ в точке N и профильную плоскость П₃ в точке Р. Точки пересечения прямой с плоскостями проекций называются следами.

 

Рис. 9

 

В пространстве точка пересечения прямой АВ, например, с горизонтальной плоскостью проекций П₁ будет точка М – пересечение АВ с ее горизонтальной проекцией А₁В₁.

На плоской модели прямоугольной системы координат сама прямая АВ отсутствует, есть только ее проекции А₁В₁, А₂В₂ и линии связи к оси Х l _X.

 

Следовательно, можно построить только горизонтальную проекцию М₁, которая совпадет с М, и фронтальную М₂.

Уравнение точки М(Х, Y, Z=0). Если точка – пересечение двух прямых, то возможна система уравнений

Z=0 - линия, совпадающая с осью Х

Z=tg j2 ´ X + Z^A - фронтальная проекция А₂В₂

 

Пересечение этих линий определит фронтальную проекцию М₂ (X ^М, Z=0).

X ^М – расстояние от начала координат до М₂.

 

Система уравнений для определения координаты Y точки М

X = X ^М - линия связи l x к оси Х через М₂

Y=tg j1 ´ X + Y^A - горизонтальная проекция А₁В₁

 

Пересечение этих линий определит горизонтальную проекцию М₁ (X ^М, Y ^М).

Y ^М – расстояние от оси Х до горизонтальной проекции М₁.

 

Фронтальный след прямой АВ – точка N(X, Y=0, Z).

 

Система уравнений для определения координаты X точки N

Y=0 - линия, совпадающая с осью Х

Y=tg j1 ´ X + Y^A - горизонтальная проекция А₁В₁

 

Пересечение этих линий определит горизонтальную проекцию N₁ (X ^N, Y =0).

X ^N – расстояние от начала координат до N₁.

 

Система уравнений для определения координаты Z точки N

X = X ^N - линия связи l x к оси Х через N₁

Z=tg j2 ´ X + Z^A - фронтальная проекция А₂В₂

 

Пересечение этих линий определит фронтальную проекцию N₂ (X ^N, Z^N).

Z ^N – расстояние от оси Х до фронтальной проекции N₂.

 

Профильный след АВ – точка Р(X=0, Y, Z).

 

Система уравнений для определения координаты Y точки P

X=0 - линия, совпадающая с осью Y

Y=tg j1 ´ X + Y^A - горизонтальная проекция А₁В₁

 

Пересечение этих линий определит горизонтальную проекцию P₁ (X=0, Y^P ).

Y ^P – расстояние от начала координат до P₁.

 

Система уравнений для определения координаты Z точки P

 

Y = Y ^P - линия связи l _Y к оси Y через P₁

Z=tg j3 ´ Y + Z^A - профильная проекция А₃В₃

 

Пересечение этих линий определит профильную проекцию P₃ (Y^P_, Z^P).

Z ^P – расстояние от P₃ до оси Y.

 

 

Длина отрезка и углы наклона к плоскостям проекций

 

Угол наклона к П₁ a прямой АВ (рис. 9) измерен между горизонтальной проекцией А₁В₁ и самой прямой АВ.

Рис. 10

 

На рис. 10 прямая задана проекциями А₁В₁ и А₂В₂.

 

Угол наклона к П₁ a можно измерить между фронтальной и горизонтальной проекциями при условии, что А₂В₂ равна АВ.

А₂В₂ = АВ ´ Соs (b) (b – угол наклона АВ к П₂)

 

Если угол b = 0, то Соs (b) =0 и А₂В₂ = АВ.

b = arctg(½Y^A - Y^B½ / A₂B₂)

Угол b = 0, если разность координат Y^A - Y^B = 0.

 

Перенесем горизонтальную проекцию во второе текущее положение А²₁В²₁ (изменятся координаты X и Y) и повернем вокруг оси Z^A (рис. 3) до положения, в котором Y^A = Y^B. Координаты Z точек А и В при этом не изменятся, т. к. траектории вращения параллельны П₁.

Фронтальные проекции точек А²₂, В²₂ будут на пересечениях линий связи к осям X и Z. Фронтальная проекция А²₂В²₂ = АВ.

Измерим a = А²₂В²₂ ^Ù А²₁В²₁.

Угол наклона к П₂ b можно измерить между горизонтальной и фронтальной проекциями при условии, что А₁В₁ равна АВ.

А₁В₁ = АВ ´ Соs (a)

Если угол a = 0, то Соs (a) =0 и А₁В₁ = АВ.

a = arctg(½Z^A - Z^B½ / A₁B₁)

Угол a = 0, если разность координат Z^A - Z^B = 0.

 

Перенесем фронтальную проекцию первое текущее положение А¹₂В¹₂ (изменятся координаты X и Z) и повернем вокруг оси Y^A (рис. 3) до положения, в котором Z^A = Z^B. Координаты Y точек А и В при этом не изменятся, т. к. траектории вращения параллельны П₂.

Горизонтальные проекции точек А¹₁, В¹₁ будут на пересечениях линий связи к осям X и Y. Горизонтальная проекция А¹₁В¹₁ = АВ.

Измерим b = А¹₁В¹₁ ^Ù А¹₂В¹₂.

 

Домашняя работа

 

 

Плоскость

 

В общем виде плоскость задана двумя пересекающимися прямыми (2). Если на этих прямых взять 3 точки, не лежащие на одной прямой, то плоскость будет задана тремя точками. Если 3 упомянутые точки соединить прямыми, то плоскость будет задана треугольником (плоской фигурой в том числе окружностью, проходящей через три точки). Если через точку на первой прямой провести прямую, параллельную второй прямой, то плоскость будет задана двумя параллельными прямыми.

 

Параметры плоскости:

База, например, точка А(X, Y, Z) в треугольнике АВС (рис. 11).

Угол a - наклон треугольника к плоскости П_1.

Угол b - наклон треугольника к плоскости П_2.

Угол g - наклон треугольника к плоскости П_3.

Перечисленные параметры считаются внешними, их изменение будет менять положение треугольника в пространстве относительно плоскостей проекций.

Натуральная величина треугольника – геометрические размеры (внутренний параметр плоскости).

Рис. 11

 

Двугранный угол между плоскостями (a ^Ù П₁, b ^Ù П₂, g ^Ù П₃) измеряется линейным углом между линиями пересечения граней этого угла

с третьей плоскостью, которая перпендикулярна данным

 

Плоскость треугольника D(АВС) на рис. 11 задана проекциями горизонтальной А₁В₁С₁ и фронтальной А₂В₂С₂.

Для определения, например, угла a можно изменить угол наклона АВС к плоскости П₂ до 90°. Треугольник АВС на плоскость П₂ спроецируется в прямую линю А¹₂В¹₂С¹₂ (рис. 11), с которой совпадет линия пересечения D¹₂ треугольника с плоскостью П₂. Плоскость П₁ перпендикулярна П₂ и плоскости пересекаются по оси Х₁₂.

Следовательно, угол a=D¹₂ ^Ù Х₁₂.

Две плоскости взаимно перпендикулярны, если одна

из них содержит перпендикуляр к другой плоскости.

Чтобы изменить угол ^A треугольника АВС, в нем надо взять прямую, угол b которой определяется на чертеже. Такой прямой может быть любая прямая, угол a которой = 0.

Возьмем прямую АD(A₂D₂, A₁D₁), координаты Z^A=X^D. A₁D₁ = AD. Следовательно, угол b ^AD = A₂D₂ ^Ù A₁D₁.

Повернем горизонтальную проекцию А₁В₁С₁ вокруг оси Z^A на угол 90° - b ^AD и перенесем в положение А¹₁В¹₁С¹₁. Проекция А¹₁D¹₁ ^ Х₁₂, при этом АD будет перпендикулярна П₂ и треугольник АВС ^ П₂. Фронтальная проекция А¹₂В¹₂С¹₂ совпадет с линией пересечения треугольника с фронтальной плоскостью D¹₂. Угол a^АВС будет измерен между D¹₂ ^Ù Х₁₂.

Натуральную величину треугольника можно найти, если расположить его, например, параллельно плоскости П₁. Повернем фронтальную проекцию А¹₂В¹₂С¹₂ треугольника вокруг оси Y^A1 на угол a^АВС и перенесем в положение А²₂В²₂С²₂. Горизонтальные проекции точек А²₁В²₁С²₁ определим на пересечении линий связи к осям Х и Y. Треугольник будет параллелен П₁. Горизонтальная проекция треугольника А²₁В²₁С²₁ равна ½АВС½.

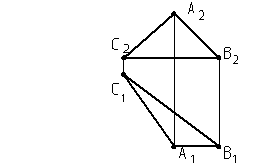
Домашняя работа

 

Определить углы a и b

треугольника АВС

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: