Поверхности, получение критериальных уравнений

Цель работы:

1. Изучение методики и получение экспериментальных значений критериев Нуссельта, коэффициентов теплоотдачи, коэффициентов сопротивления по длине, потерь давления для исследуемой теплопередающей поверхности.

2. Обработка экспериментальных данных, получение критериальных уравнений.

 

Многообразие условий охлаждения сжатого газа и других теплоносителей в компрессорных, холодильных, технологических установках и системах кондиционирования требует использования теплообменных аппаратов (ТА) разнообразных конструкций. Их проектирование является важнейшим этапом жизненного цикла теплообменного оборудования, основой которого в свою очередь служат различные виды расчетов. Прежде всего это проектные и поверочные расчеты теплообменных аппаратов, которые содержат в свою очередь тепловые, гидромеханические, конструктивные, экономические, прочностные и оптимизационные. Расчеты основаны на соответствующих математических моделях. Универсальная математическая модель рекуперативных ТА может быть записана в виде системы уравнений: переноса количества движения, сплошности, переноса энергии (тепла), переноса тепла в твердом теле, состояния теплообменивающихся сред, уравнений теплофизических свойств и граничных условий. Данная математическая модель, учитывающая изменение теплофизических характеристик многомерного нестационарного процесса теплообмена, позволяет провести наиболее точные численные исследования работы теплообменных аппаратов. Однако в настоящее время решение таких сопряженных задач связано с преодолением значительных математических и технических трудностей. Поэтому при расчете ТА принимается ряд упрощающих допущений и, в частности, проводится декомпозиция (отдельное рассмотрение) задач течения и переноса энергии (тепла).

Разрывая связь между влиянием сил вязкости на распределение скоростей в потоке (прежде всего в пограничном слое) и на теплообмен между теплоносителем и твердым телом, вводится коэффициент теплоотдачи a, определяющий условие равенства потока тепла, отданного движущимся теплоносителем и воспринятого твердым телом. Вводится также коэффициент гидравлического сопротивления x. Таким образом, сложность теоретических проблем совместного решения систем диффуравнений заменяется проблемами определения эмпирических зависимостей коэффициентов теплоотдачи a и сопротивления x в каналах различной геометрии с определяющими параметрами (критериями) в форме корреляционно-статических уравнений множественной регрессии Nu=f(Re,Pr,…), x=f(Re).

Здесь Nu – критерий Нуссельта, характеризующий меру отношения теплового потока, передаваемого конвекцией в направлении по нормали к поверхности стенки – к тепловому потоку, передаваемому путем теплопроводности через пограничный слой. Re – критерий Рейнольдса, характеризующий соотношение между инерционными силами и силами трения, определяющий наиболее важные свойства течения среды, например, режим течения. Pr – критерий Прандтля, определяющий подобие температурных и скоростных полей в потоке.

При обобщении экспериментальных данных, наряду с критерием Нуссельта, используется также критерий Стентона St=Nu/RePr, который можно рассматривать как отношение удельного потока теплообмена среды с поверхности к удельному потоку конвективного переноса тепла средой. Тогда St=q_s/q_конв=aÑT/Mc_pÑT, или St=a/wc_pr.

 

Если информации о моделируемом объекте (процессе) недостаточно или он настолько сложен (имеет случайный характер), что невозможно составить его детерминированную модель, используют стохастические модели и соответствующие экспериментально-статистические методы.

На практике весьма распространенной является задача определения функции (аналитической зависимости), которая должна соответствовать некоторым данным, полученным, например, при проведении экспериментальных исследований. При этом можно выделить два направления приближения функции – процесс интерполяции, определяющий вид функции, совпадающей с табличными данными, а также процесс аппроксимации, направленный на восстановление функциональной зависимости по данным эксперимента, возможно содержащего ошибки. Аппроксимация при этом должна обеспечивать оптимальное расположение линии (поверхности для многофакторного эксперимента) функции среди множества экспериментальных точек, не обязательно совпадающей с ними.

Наиболее употребительным способом аппроксимации данных, содержащих ошибки, является метод наименьших квадратов. Он позволяет определить вид функции (в виде регрессии) с минимальной суммой квадратов отклонений ее значений от экспериментальных. В общем случае задача аппроксимации данных решается для нелинейной функции многих переменных.

Так как в реальном процессе всегда существуют неуправляемые и неконтролируемые переменные, результат эксперимента есть случайная величина. Пусть, например, требуется исследовать зависимость y(x₁, x₂,…x_m), причем величины y и Х={x₁, x₂,…x_m} измеряются в одних и тех же экспериментах. Будем считать, что величины x_j измеряются точно, в то время как измерение величины y содержит случайные погрешности. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(X), зависящей от X, как от параметра.

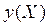Регрессией называют зависимость условного математического ожидания величины h(X) от переменной X. Задача регрессионного анализа состоит в этом случае в восстановлении функциональной зависимости по результатам измерений (X_i, y_i), i=1,2,…, N. Аппроксимируем неизвестную зависимость при помощи заданной функции уравнения регрессии . Это значит, что результаты измерений можно представить в виде , где – неизвестные параметры регрессии, z_i – случайные величины, характеризующие погрешности эксперимента. С учетом разложения исследуемой зависимости в ряд Тейлора в окрестности X₀ и использования выборочных коэффициентов , как оценок теоретических (b₀=f(X₀), b₁=¶ f(X₀)/¶ x₁,…) уравнение регрессии можно записать в следующем общем виде [7]

 

(3.1)

 

где b₀ – свободный член уравнения регрессии; b_j – линейные эффекты; b_jj – квадратичные эффекты; b_jk – эффекты взаимодействия.

Коэффициенты уравнения (3.1) определяются методом наименьших квадратов

 

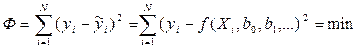, (3.2)

 

где N – объем выборки.

Необходимым условием минимума является равенство нулю соответствующих частных производных , . Тогда после преобразования получим

 

(3.3)

 

Система (3.3) содержит столько же уравнений, сколько неизвестных коэффициентов входит в уравнение регрессии и называется в математической статистике системой нормальных уравнений. Для решения системы (3.3) необходимо задать конкретный вид функции .

 

Обычно после обработки экспериментальных данных для теплогидравлических характеристик теплопередающих поверхностей получают критериальные уравнения в виде:

– для оценки интенсивности теплообмена при помощи критерия Нуссельта Nu (характеризует меру отношения теплового потока, передаваемого конвекцией в направлении по нормали к поверхности стенки – к тепловому потоку, передаваемому путем теплопроводности через пограничный слой)

 

; (3.4)

 

– для оценки уровня гидравлического сопротивления

 

. (3.5)

 

С учетом упрощений и принимая значение критерия Прандтля для сжатого воздуха Pr=0.76 (примерно соответствует 70-80 ºС) и =0,33 выражение (3.4) можно преобразовать к виду

 

. (3.6)

 

Таким образом, и для критерия Нуссельта Nu и для коэффициента гидравлического сопротивления x искомые зависимости можно представить в виде трансцендентной регрессии одного параметра дробно-степенного типа . Вычисления данного вида регрессии можно упростить, если провести замену переменных и линеаризовать приведенные выше зависимости путем логарифмирования:

 

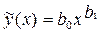à à , (3.7)

 

где , .

Коэффициенты в выражении (3.7) уже для линейной регрессии определяются методом наименьших квадратов, значения которых далее используются для нахождения [1].

Искомые коэффициенты для уравнения регрессии можно найти и при помощи средств MATLAB.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: