Расчет системных характеристик экспоненциальных СеМО

Характеристики СеМО определяются обычно на уровне средних значений и делятся на локальные и системные. К локальным характеристикам СеМО откосятся характеристики всех входящих в нее CМО (рассмотрены в п. 1.4.1). Системные характеристики отражают свойства сети в целом, рассматриваемой как единая, неделимая на части система.

Наиболее важными системными характеристиками СеМО являются:

1) Среднее время пребывания в сети. Временем пребывания в сети называется время между приходом заявки в сеть и ее уходом из сети.

2) Передаточные коэффициенты . Пусть заявка входит в сеть из i -го входного потока. Её маршрут в сети случаен, поэтому случайно и число приходов в j -ю СМО за время пребывания в сети. Среднее значение a _ij этого числа приходов будем называть передаточным коэффициентом. Он однозначно определяется для любых i, j, матрицей Р вероятностей передач.

3) Входовые средние времена F₁,...,F _N пребывания в сети. Величина F_j определяется как среднее время пребывания в сети заявки, поступающей из j -го входного потока .

4) Условные пропускные способности B₁,...,B _N. Предположим, что в заданной СеМО значение интенсивности I _j заменено на максимальное значение, при котором сеть ещё стационарна. Это значение B _j будем называть условной пропускной способностью по входу j.

При заданных I _k (k ¹ j) сеть стационарна для любых значений I _j £ B _j.

5) Абсолютные пропускные способности A _j. Предположим, что в заданной СеМО интенсивности всех входных потоков, кроме j -го, заменены на нулевые, а I _j заменена на предельное значение, при котором сеть ещё стационарна. Это значение B _j будем называть абсолютной пропускной способностью по j -му входу.

Если I _j > A _j, то сеть нестационарна, каковы бы ни были интенсивности остальных входных потоков.

6) Запасы D₁,...,D_N по пропускным способностям. Запас 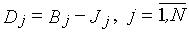. Запас D_j показывает, насколько может быть увеличена интенсивность прихода заявок на j -м входе (при заданных остальных) без нарушения условия стационарности.

Если в виде СеМО моделируется некоторая реальная система, то характеристики 1 - 6 могут дать ценную информацию о свойствах этой реальной системы. Например, если СеМО изображает вычислительную систему реального времени, то среднее время пребывания Е характеризует среднее время ответа системы, а запасы D_i выражают готовность системы продолжать устойчивое функционирование при увеличении нагрузки (интенсивности запросов) по тому или иному входу.

Среднее время пребывания заявки в СеМО рассчитывается по формуле

,
(2.3)

где I = I₁ +,...,+ I _N. Эта формула выводится ниже.

Для СеМО (рис. 6)

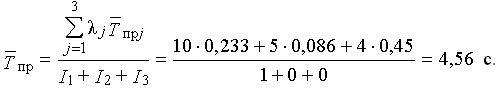
Передаточные коэффициенты

Важное и полезное свойство передаточных коэффициентов состоит в следующем. В стационарном режиме при любых I₁ +,...,+ I _N для l₁,...,l _N справедливо

(2.4)

Обратим внимание на то, что строка передаточных коэффициентов в (2.4) представляет собой столбец матрицы ||a _ij ||. Система (2.4) выражает интенсивности l _j прихода заявок в СМО через интенсивности I₁ +,...,+ I _N входных потоков сети.

Значения коэффициентов a _ij однозначно определяются матрицей Р вероятностей передач. Из (2.4) вытекает, что при I₂ =... = I _N = 0, I₁ = 1имеет место

(2.5)

Это позволяет найти строку коэффициентов a _{1 j} - матрицы ||a _ij || путем решения уравнений баланса сети для случая I₁ = 1, I₂ =... = I _N = 0: согласно (2.5), найденные значения l₁,...,l _N будут численно равны коэффициентам a ₁₁,..., a _{1 N} . Аналогично для случая, когда I _k =1, остальные I _i = 0. Решение уравнений баланса даст значения a _{k 1},..., a _kN. Исходя из этого, можно рекомендовать следующий алгоритм вычисления матрицы ||a _ij ||.

1) Составить уравнения баланса сети, включающие интенсивности I ₁,… I_N в буквенном виде.

2) Положить k =1.

3) Решить уравнения баланса для случая, когда I _k =1, остальные I _i = 0. Полученные значения l₁,...,l _N записать в k -ю строку матрицы передаточных коэффициентов.

4) Положить k = k +1.

5) Если k < N, перейти к шагу 3, иначе к шагу 6.

6) Конец.

Найдем, например, матрицу ||a _ij || для CeМO (рис.6), составим уравнения баланса:

(2.6)

Решим эти уравнения для I ₁=1, I ₂= I ₃=0. Получим l₁=10, l₂=5, l₃=4. Для I ₂=1, I ₁= I ₃=0 решением будет l₁=10, l₂=6, l₃=4 и для I₃=1, I₁=I₂=0 получаем l₁=10, l₂=5, l₃=5.

Следовательно, матрица ||a _ij || этой СеМО имеет вид:

Свойства суммы, смеси и суммы случайного числа слагаемых

Среднее значение суммы случайных величин равно сумме их средних, для y = x₁+...+x _n справедливо

M(y) = M(x₁)+...+M(x _n) (2.8)

Смесью случайных величин х ₁,..., х_n называется величина z, которая принимает значение х ₁ с вероятностью р ₁, х_n - с вероятностью р_n.

Выбор i -й случайной величины х_i и ее значение статистически независимы.

Смесь обладает следующим свойством:

M(y) = p ₁M(x₁)+...+ p_n M(x _n). (2.9)

Свойства суммы и смеси легко выводятся из определения понятий функции распределения вероятностей и математического ожидания.

Суммой t случайного числа слагаемых назовем сумму вида;

 

число g слагаемых случайно; x_i - независимые случайные величины с одинаковыми средними t = х ₁,..., х _g. Тогда

M (t)= M (g) M (x). (2.10)

Свойство (2.10) выводится из (2.8) и (2.9).

Входовое среднее время пребывания

Рассмотрим СеМО (рис. 6) и проследим, как. формируется входовое время пребывания в сети заявки первого потока. Видно, что это время состоит из двух слагаемых. Первое слагаемое есть время пребывания в СМО1, составляющее в среднем . Второе слагаемое с вероятностью р ₁₀ равно нулю (заявка уходит из сети), с вероятностью р ₁₂ равно входовому времени пребывания для входа 2 (заявка входит в сеть через СМО2) и с вероятностью р ₁₃ - входовому времени пребывания для входа 3.

Из свойства смеси вытекает, что в среднем второе слагаемое составляет величину

p ₁₀ · 0 + p ₁₂F₂ + p ₁₃F₃ = p ₁₂F₂ + p ₁₃F₃.

В целом среднее входовое время пребывания F ₁ по свойству суммы равно сумме средних значений первого и второго слагаемых:

F₁=T_пр1+ p ₁₂F₂+ p ₁₃F₃. (2.11)

Рассуждая аналогично о входовых средних временах пребывания F ₂ и F ₃ можно записать для них сходные с (2.11) уравнения, которые вместе с (2.11) составят следующую систему уравнений:

(2.12)

Из этой системы при известных (найденных при расчете схемы на рис. 6) нетрудно найти F ₁ = 4,56; F ₂ = 4,64; F ₃ = 5,01.

По аналогии с (2.10) можно составить уравнения относительно F _i для.любой экспоненциальной СеМО.

Характеристики F_i могут быть вычислены и без (2.10) по формуле

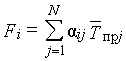. (2.13)

В этом случае уравнения вида (2.12) можно использовать для проверки правильности вычислений, произведенных по (2.13).

Формулу (2.13) можно вывести следующим образом. Пусть заявка входит в СеМО по i -му входу. Ee среднее число посещений j -й СМО есть a _ij. При каждом посещении заявка задерживается в среднем на время . По свойству суммы случайного числа слагаемых суммарное время, проведенное заявкой в j- й СМО, составит a _ij · . Общее время пребывания заявки в СеМО складывается из времен, проведенных в каждой СМО. По свойству суммы из этого вытекает (2.13).

Выведем теперь формулу для вычисления среднего времени пребывания в сети. Это среднее определяется для произвольной приходящей в сеть заявки без различения того, по какому входу она поступает.

Пусть р ₁ для такой заявки означает вероятность того, что она вошла по входу 1, …, р _N – вероятность того, что она вошла по входу N.
Из свойства смеси .

Поскольку p_i = I _i /I, где I = I₁+...+I _N, то

.

Подставляя сюда (2.13) и меняя порядок суммирования слагаемых, получим

.

Согласно (2.4), сумма по i представяяет здесь l _j , oткуда вытекает (2.3).

Развернутая форма условия стационарност

Условие стационарности СеМО эапишем в виде .

Эта запись эквивалентна следующей: .

Выражая l _j через I _j по формуле (2.4), получим развернутую форму условия стационарности:

(2.14)

Эта система неравенств эквивалентна (2.2).

Для конкретных СеМО некоторые из неравенств (2.14) оказываются излишними: такие неравенства можно исключать из (2.14), не изменяя решения системы. Например, для СеМО (рис. 6) условие (2.14) примет вид

(2.15)

или, после сокращения на положительные коэффициенты,

(2.16)

В этой системе второе неравенство вытекает из первого (сравните их,
предварительно умножив первое на 1,2). Поэтому второе неравенство может быть отброшено. Кроме того, первое неравенство вытекает из третьего, поэтому его тоже можно отбросить. Следовательно, условие стационарности (2.16) эквивалентно следующему:

I₁+I₂+1,25I₃£10/ 7. (2.17)

Абсолютная пропускная способность

Используя развернутую форму условий стационарности, абсолютную пропускную способность A_j по i -му входу можно найти непосредственно по ее определению. Действительно, если все входные интенсивности СеМО, кроме I_i, положить равными нулю, то из (2.14) получим, что для стационарности необходимо условие:

Это условие удобно переписать так:

(2.18)

Из определения A_i вытекает, что эта величина равна максимальному из значений I_i, отвечающих (2.18). Следовательно, A_i равно наименьшей из правых частей в (2.18). Для СеМО (рис.6) нахождение A_i несколько упрощается благодаря тому, что условие стационарности сети (2.17) содержит лишь одно неравенство. Так, полагая I ₂ = I ₃ =0 для I ₁ из (2.17) получим I ₁ £ 10 / 7, откуда А ₁= 10/7. Аналогично вычисляются А ₂ = 10/7 и А ₃ = 8/7. Вполне естественно, что найденные значения совпадают с максимальными значениями для I_i, показанными в правых частях (2.16).

Условная пропускная способность

Условная пропускная способность, как и абсолютная, может быть найдена из (2.14). Для нахождения B_i в (2.14) следует подставить заданные значения всех входных интенсивностей СеМО, кроме I_j. Затем полученная система разрешается относительно I_i в виде

(2.19)

и B_i находится как наименьшая из правых частой в (2.19). Если условие стационарности СеМО содержит лишь одно неравенство (рис. 5), то нахождение B_i упрощается. Из (2.17) для упомянутой СеМО найдем, что В ₁ = 10/7, В ₂ = 3/7, В ₃= 12/35.

Запасы по пропускным способностям

Формула для вычисления запасов D_i дана непосредственно в их определении. Для СеМО (Рис.6) запасы составляют D ₁ = 10/7-1=3/7, D ₂ = 3/7-0=3/7, D ₃= 12/35-0=12/35.

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: