Задачи для самостоятельного решения

Лабораторный практикум

По курсу

«Надежность электрооборудования

Электроэнергетических систем»

Учебное пособие

для студентов специальностей

«Электротехнические системы электропотребления»

и «Электрические станции»

очной и заочной форм обучения

 

Утверждено

Ученым советом университета

 

СЕВАСТОПОЛЬ

621.31

А 674

УДК 621.31.019:621.311

Омельченко Н.В.

А 674 Лабораторный практикум по курсу надежность электрооборудования электрических станций: Учеб. пособие. - Севастополь: СНУЯЭиП, 2012. - 105 с.: ил.

 

В данном учебном пособии излагаются вопросы теории надежности электрооборудования электрических станций путем решения практических задач и выполнения лабораторных работ по разделам курса надежность электрооборудования электрических станций для студентов специальности «Электрические станции» очной и заочной форм обучения.

Отличительной особенностью пособия является то, что в нем кратко изложены теоретические основы исследования показателей надежности элементов электрооборудования по методу доверительных интервалов, методология проверки гипотезы о законе распределения случайной величины с целью оценки возможности продления срока службы электрооборудования, а также предложен алгоритм расчета ЗИПа методом оптимизации при ограничении по «стоимости» ЗИПа.

Лабораторные работы носят исследовательский характер. В процессе их выполнения изучаются особенности точечных и интервальных оценок показателей надежности, свойства и эффективность различных методов повышения надежности. Особое место занимают задачи, посвященные проблеме продления срока эксплуатации оборудования.

Предназначено для студентов Севастопольского национального университета ядерной энергии и промышленности очной и заочной форм обучения.

Рецензенты:

О.Ю.Анисимов

М.Б.Углова

 

© Издание СНУЯЭиП, 2012

ЦЕЛИ И ЗАДАЧИ ЛАБОРАТОРНОГО ПРАКТИКУМА

 

Источник знаний, и притом единственный, — это наука. Лабораторные работы являются тем источником, который содержит начальные элементы научных исследований. Можно хорошо изучить теорию надежности и даже уметь решать задачи, доведя их решение до численного ответа, но не видеть проблем в теории и практике надежности, не уметь формулировать задачу. Всему этому учит лабораторный практикум.

Студент, выполняя лабораторную работу, учится ставить задачу, выбирает метод и компьютерные технологии ее решения. Анализ полученных результатов позволяет выяснить физическую сущность процессов, протекающих в исследуемой системе.

Лабораторный практикум преследует следующие цели:

· подтверждение теоретических положений, высказанных преподавателем на лекциях;

· ознакомление студента с методами научных исследований;

· изучение компьютерных технологий и приобретение навыков решения задач надежности, которые не могут быть изложены на лекциях;

· изложение физической сущности процессов, в смысле надежности, протекающих в технических и информационных системах.

Лабораторный практикум состоит из 3 лабораторных работ исследовательского характера.

Основные особенности данного практикума:

· исследовательский характер всех лабораторных работ;

· исследование надежности технических и информационных систем при произвольных законах распределения отказов и восстановлений;

· многовариантность задач в каждой лабораторной работе, обеспечивающих индивидуализацию обучения;

· необходимость представления решений в аналитическом, численном и графическом виде;

· наличие в описании каждой лабораторной работы примера ее выполнения.

По каждой выполненной лабораторной работе студент представляет отчет, который должен содержать следующие пункты:

1. постановка задачи;

2. модели и алгоритмы решения задачи;

3. краткое изложение методики выполнения работы;

4. решение задачи в виде формул, таблиц, графиков;

5. анализ полученных результатов и основные выводы.

 

Лабораторная работа № 1

Статистическая оценка числовых характеристик непрерывных и дискретных случайных величин, используемых в теории надежности

 

Постановка задачи

· По статистике отказов изделия определить точечную и интервальную оценки неизвестной вероятности отказа изделия исходя из биноминального распределения частоты отказов изделия в интервале времени (t..Δt).

· С учетом экспоненциального распределения случайной величины Т, определить доверительные границы интенсивности отказа изделия для заданной доверительной вероятности ₂.

 

Сведения из теории

Эксплуатация оборудования сложных электроэнергетических систем представляет собой наиболее информативный вид испытаний на надежность, так как при этом оборудование подвергается такому широкому спектру внешних воздействий, режимов работы и обслуживания, который невозможно воссоздать в искусственных условиях.

Процесс обработки эксплуатационной информации состоит из двух частей: этапа предварительной обработки и этапа окончательной (математической) обработки. В основе предварительной обработки ле­жит классификация нарушений работоспособности оборудования — разделение массива информации на три группы: конструкционные, про­изводственные и эксплуатационные отказы. Классификация отказов требует глубокого знания принципов функционирования и специфики эксплуатации оборудования. Классификация не всегда может быть од­нозначной. На основании данных об отказах формируют выборки, пред­назначенные для последующей математической обработки.

Классические методы математической статистики для анализа эксплуатационной информации о надежности объектов

Случайными величинами, которые подвергаются обработ­ка по эксплуатационной информации в картах неисправностей обору­дования, являются наработка до отказа, наработка на отказ, наработка до предельного состояния, время восстановления, число отказов, число восстановлений, т. е. непрерывные и дискретные случайные величины Х = {х₁, х₂,..., х_n}, где значения х_i i = 1…n, называются выборкой из генеральной совокупности N или просто выборкой, каждое отдельное значение Х — элемен­том выборки, а общее количество элементов n — объемом выборки.

Предполагается, что число членов N в генеральной совокупности велико, а объем выборки n ограничен (n «N). Обычно используется математическая идеализация, состоящая в том, что генеральная сово­купность считается бесконечной (N →∞). При этом точные (теоретиче­ские) характеристики случайной величины (закон распределения, мате­матическое ожидание, дисперсия и др.), относящиеся к генеральной совокупности, отличаются от аналогичных им выборочных (статистиче­ских) характеристик (статистических оценок) из-за ограниченности объема выборки n. Если n неограниченно возрастает, то все выбороч­ные характеристики приближаются (сходятся по вероятности) к соот­ветствующим характеристикам генеральной совокупности. Выборочные характеристики в отличие от характеристик генеральной совокупности являются случайными величинами.

Первичный статический материал при дальнейшей обработке обыч­но представляют в виде вариационного или статистического рядов. Ва­риационный ряд представляет собой совокупность упорядоченных значе­ний случайной величины вида х₁ <х₂ <х... <х_n. Если число наблюдений достаточно большое (более 50), то запись статистического материала в виде вариационного ряда становится громоздкой и мало наглядной (это замечание справедливо для ручной обработки информации и несущест­венно при записи ее на магнитных носителях). Статистическим рядом(или гистограммой) называется таблица, в которой приведены интерва­лы в порядке их расположения на числовой оси и соответствующие им частоты (частости)

где m_i — число значений случайной величины в i -м интервале.

Группировка по 10...20 интервалов, в каждый из которых попадает не более 15...20% значений случайной величины, обычно оказывается достаточной для полного выявления всех существенных свойств распределения и достоверного вычисления основных числовых характеристик случайной величины.

Если выборка однородна и достаточно большая, то с помощью ва­риационного и статистического рядов легко определяются статистиче­ские оценки показателей надежности.

Членами вариационного ряда могут быть либо наработка на отказ (или до отказа), либо время восстановле­ния, которые записываются в порядке возрастания от 1-го до k -го членов.

Как известно, наиболее полной характеристикой любой случайной величины являются их законы распределения, которые устанавливают связь между возможными значениями случайной величины и соответствующими им вероятностями.

При оценке надежности изделия на практике, как правило, закон распределения величины, характеризующей его надежность, точно не известен. Возникает задача о принятии гипотезы о законе распределения и практическом получении его параметров, точное значение которых тоже неизвестно.

Задачу по оценке параметров закона распределения сформулируем так: получить оценку, близкую к истинному значению оцениваемого параметра.

Эта задача решается с использованием точечных и интервальных оценок.

Точечные оценки параметров выбранного закона распределения. Оценкой параметра называется его значение, найденное по выборке, т.е. по ограниченному числу наблю­дений. Если оценкой параметра является число, то такие оценки назы­ваются точечными. Если же оценкой служит совокупность чисел (ин­тервал на числовой оси), то оценки называются интервальными.

Точечные оценки количественных показателей надежности при экс­поненциальном законе распределения применяются для непрерывных случайных величин, таких как средняя наработка до отказа, средняя наработка на отказ наработки и среднее время восстанов­ления. Их можно получить из выражений:

, где λ – интенсивность отказов;

, где ν - интенсивность восстановлений.

 

Для дискретных случайных величин (целых чисел), таких как точечные оценки вероятности отказа или вероятности безотказной работы при определенных условиях характерен биномиальный закон распределения (ступенчатая ломаная функция). Выражения для таких оценок приведены ниже.

Интервальные оценки параметров закона распределения.

В математической статистике разработаны точные и приближенные методы построения доверительных интервалов для параметров случайной величины. Точные методы требуют знания закона распределения случайной величины T. При использовании приближенных методов это необязательно.

Интерваль­ная оценка представляет собой случайный интервал, который с некоторой доверительной вероятностью накрывает оцениваемый параметр θ. Этот интервал называется доверительным интервалом, границы интервала — довери­тельными границами, вероятность, с какой доверительный интервал на­крывает параметр θ - доверительной вероятностью. Для заданной ве­роятности a по выборке х_i, i = 1,...,n случайной величины Х могут быть найдены такие значения случайных величин и 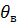, при которых

· интервал от до +∞ накроет параметр θ с вероятностью P(θ≥θ_н)=α₁;

· интервал от - ∞ до θ_В накроет параметр θ с вероятностью Р(θ≤0_В)=α₂.

Величины θ_Н и θ_В называются, соответственно, нижней и верхней доверительной границей для параметра θ; θ_Н и θ_В образуют доверитель­ный интервал для параметра θ при двусторонней доверительной вероят­ности _2.

В общем виде эта зависимость имеет вид = Р(θ_н ≤ θ ≤ θ_в).

При этом, чем больше доверительная вероятность , тем шире границы интервала и наоборот. Вероятность того, что значение θ выйдет за гра­ницы интервала (θ_Н, θ_В), называется уровнем значимости :

= Р(θ_Н > θ > θ_В) = 1 - .

Значения доверительных вероятностей обычно принимают равными 0,9; 0,95; 0,99. Соответствующие им уровни значимости составляют 0,1; 0,05; 0,01.

 

При реальной эксплуатации оборудования сложных систем п «∞, Т« ∞. Поэтому точечные и интервальные оценки показателей надеж­ности оборудования зависят от плана испытаний. В таблице 1.1[5] приведе­ны выражения для расчета точечной (средней) оценки интенсивности отка­зов, а также нижней и верхней границ интенсивности отказов λ_Н и λ_В для различных планов испытаний. Напомним, что буквы плана рас­шифровываются следующим образом: первая буква m — объем выборки; вторая буква Б или В — без восстановления или с восстановлением выборки; третья буква — t₀ или n — признак окончания наблюдений, причем t₀ — после истечения заданного времени, n — после появле­ния установленного числа отказов. Для определения границ λ необхо­димо пользоваться таблицей квантилей χ² -распределения [6], в которой да­ются доверительные вероятности (1 — ₁) или ₂ и число степеней свободы k, равное 2п, 2n+2 в зависимости от выбранного плана. Значение задается в зависимости от требований, предъяв­ляемых к системе.

Экспоненциальное распределение является однопараметрическим.

Для получения статистической оценки надежности изделия с заданной точностью и достоверностью необходимо располагать достоверной статистикой в нужном количестве, что не всегда возможно. Особенно часто такая ситуация создается при оценке надежности сложных, уникальных систем или при оценке исключительно надежных систем.

 

Таблица 1.1

Используя таблицу 1.1 [5] можно рассчитать значения показателей надеж­ности в зависимости от плана испытаний при экспоненциальном законе распределения χ² (1-α₁), 2n и χ² (α₂), 2n(2n+2) – Q% -е точки χ² распределения с 2n (2n+2) степенями свободы, определяемые по табл. 2.2,а [6].

 

Код входа в таблицу 2.2,а

 

2d(2d+2)=2n(2n+2) ----> n; χ² (α₂)= (1+δ₂)/2] ----> Q_Н(табл.)

2d=2n ----> n; χ² (1-α₁)= (1-δ₂)/2] ----> Q_В(табл.)

P_Н(t)= = ; T_0Н= ; P_В(t)= = ; T_0В= ;

 

 

Таблица 1.1

План	Интенсивность отказов
λ *	λВ	λН
[mBto]
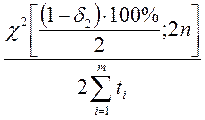
[mBn]

 

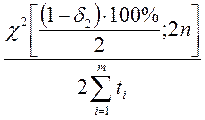
Под точностью количественного показателя надежности будем понимать ширину доверительного интервала, накрывающего данный показатель, а под достоверностью - доверительную вероятность этого результата.

Граница между принципиальной возможностью количественной оценки надежности и практической невозможностью ее получения как раз и устанавливается при имеющейся статистике той конкретной величиной точности и достоверности, которые будут признаны необходимыми для данного технического устройства.

Эту мысль проще всего разъяснить на примере конкретной количественной характеристики надежности вероятности отказа Q(t).

Будем считать отказ случайным событием, которое при неоднократном воспроизведении одного и того же опыта может произойти или не произойти. В целях оценки безотказности изделия нужно c отказом связать определенное число, которое тем больше, чем более возможен отказ. Такое число называют вероятностью отказа.

Понятие вероятности отказа в своей основе связано с понятием частоты (частости) отказа Q^*(t, Δt).

, (1.1)

где n(t,Δt) - число отказов на интервале времени (t...t+Δt);

m(t) - общее число объектов, за которыми установлено наблюдение, в момент времени t.

При небольшом числе опытов m частость отказов носит в значительной мере случайный характер и может заметно изменяться от одной группы опытов к другой. Однако при увеличении числа опытов частость отказов теряет свой случайный характер и проявляет тенденцию стабилизироваться, приближаясь к некоторой величине. Естественно предположить, что эта величина и есть вероятность отказа. На практике частость отказов при достаточно большом числе опытов принимают за приближенное значение вероятности отказа.

Достоверность и объективная ценность всех практических расчетов надежности, выполненных с применением теории вероятностей, определяется качеством и количеством экспериментальных данных, на базе которых этот расчет производится.

Доверительные интервалы для вероятности отказа

Если надежность изделия характеризуется показателем вероятности безотказной работы и условия испытания (эксплуатации) изделий не позволяют определить моменты возникновения их отказов и m(t) < = 500, а число отказов n(t,Δt) относительно небольшое, то частота отказов Q^*(t,Δt) имеет биномиальный закон распределения. На этой закономерности построены точные способы определения доверительных границ вероятности отказа.

1. В работе Большев Л.Н., Смирнов Н.В Таблицы математической статистики. - М.: Наука, 1983 приведена таблица 5.2, которая содержит заранее вычисленные значения Qв и Qн с точностью до трех десятичных знаков. Табл. 5.2 рассчитана до m < = 500 и для δ₂ = 0.9; 0.95; 0.99.

Коды входа в таблицу 5.2

наша информация		таблица
δ2	→	2P-1
число отказов n	→	μ
число исследуемых объектов m	→	n
разность m-n	→	n-μ

Пример 1.

Определить доверительные границы вероятности отказа изделий в интервале времени 0...10000 часов, если известно, что за первые 10000 часов наблюдения из 684 изделий отказало 15.

Задаемся доверительной вероятностью δ₂ = 0,95.

Решение

Частота отказов Q^* (0...10000) = n/m = 15/684 = 0,0219 = 0,022

Для входа в таблицу 5.2 определим величины:

2Р-1 = 0,95

μ = 15

n - μ = 684-15 = 669

 

Так как значащие интервалы в табл. 5.2 заканчиваются на числе 500, то можно сказать, что в данном случае доверительные границы будут не больше, чем Q_В (0...10000) = 0,047; Q_Н( 0...10000) = 0,016, а интервальная оценка вероятности отказа изделия запишется так:

0,016 < Q (0...10000) < 0,047

При доверительных вероятностях δ₂ = 0,99 и 0.9 интервальные оценки будут соответственно равны:

Q_В (0...10000) = 0,054; Q_В (0...10000) = 0,044;

Q_Н (0...10000) = 0,013; Q_Н (0...10000) = 0,018;

 

0,013 < Q (0...10000) < 0,054

0,018 < Q (0...10000) < 0,044

 

В тех случаях, когда по условиям задачи числа n и m не совпадают с табличными величинами или m > 500, или требуемая точность расчета превышает три десятичных знака, или δ₂ <> 0.9; 0.95; 0.99, доверительные границы необходимо вычислять.

Точные способы определения доверительных границ для неизвестной вероятности отказа разработаны, исходя из того, что частота отказов как дискретная случайная величина подчиняется биномиальному закону распределения.

Как показывает опыт расчетов, табл. 5.2 из работы [6] часто бывает недостаточно. В этом случае квантили B-распределения можно определить из асимптотических формул, полученных Л.Н. Большевым. Из этих формул получены асимптотические формулы для определения доверительных границ Q_В и Q_Н, в которые входят Q -процентные точки χ² -распределения с k = 2n и 2(n+1) степенями свободы, определяемые по табл. 2.2,а [6].

Код входа в табл. 2.2,а:

1. верхняя граница 2(n+1) → n; 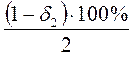→ Q_В(табл.)

2. нижняя граница 2n → n; → Q_Н(табл.)

В явном виде доверительные границы вычисляются по формулам:

 

Q_В ≈ 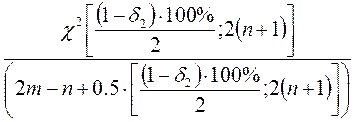(1.2)

Q_Н ≈ (1.3)

 

Пример 2.

За 8760 часов наработки изделий получена статистика по отказам:

m = 15; n = 4. С доверительной вероятностью δ₂ = 0.95 определить точечную и интервальную оценки вероятности отказа изделия за указанное время.

Решение:

 

Частота отказов Q^* (0...8760) = 4/15 = 0,2666.

По табл. 2.2,а определяем

 

 

Интервальная оценка вероятности отказа изделия в этом случае запишется так: 0.0776 < = Q (0...8760) < = 0.5652.

На практике часто приходится встречаться с задачей определения доверительного интервала для вероятности отказа, когда полученная из опыта или по данным эксплуатации частота отказов равна нулю. В этом случае для оценки надежности изделий также применим точный метод построения доверительного интервала на основе биномиального распределения. В этом случае верхняя доверительная граница вероятности отказа определяется выражением:

 

= (1.4)

Пример 3.

Пусть за время испытаний (0,t) не отказал ни один из 10 электродвигателей. Спрашивается, какова их надежность в плане безотказности?

Задавшись коэффициентом доверия δ₁ = 0.90, определим верхнюю доверительную границу:

Таким образом, если за время испытаний не возникло ни одного отказа, то с гарантией 90 % можно утверждать, что вероятность отказа данных электродвигателей не превышает 0.206 (при m = 10).

 

Вывод.

Рассмотренные примеры наглядно показывают, что при использовании вероятностных критериев при оценке надежности предполагается применение более жестких условий контроля, чем в том случае, когда заказчик выдвигает требование так называемой 100%-й надежности, а на практике довольствуется безотказной работой в течение времени t малого числа изделий (иногда даже одного).

Задачи для самостоятельного решения

Задача 1.1.

Производились испытания на надежность (велись наблюдения при эксплуатации) группы из m одинаковых изделий по методу доверительных интервалов. Испытания (наблюдения) были прекращены в момент появления n -го отказа. Эти отказы наблюдались за время t_n = 1000 часов.

Определить в пересчете на одно изделие λ^*; границы двухстороннего доверительного интервала λ_Н и λ_В при δ₂ = 0.95.

Методическое указание: использовать таблицу 1.2. для вариантов задания и для расчетов таблицы 1.1 [5] и 2.2,а [6].

 

Таблица 1.2 вариантов задания

Nп/п	m	n	Nп/п	m	n	Nп/п	m	n

 

 

Задача 1.2.

Производились испытания на надежность (велись наблюдения при эксплуатации) группы из m одинаковых изделий по методу доверительных интервалов. Испытания (наблюдения) были прекращены через 1000 часов. В течение заданного заранее интервала времени наблюдалось n отказов.

Определить в пересчете на одно изделие λ^*; границы двухстороннего доверительного интервала λ_Н и λ_В при δ₂ = 0.99.

Методическое указание: использовать таблицы для вариантов задания 1.2 и для расчетов 1.1[5] и 2.2,а [6].

Задача 1.3.

Определить продолжительность испытаний изделия, которые должны подтвердить с доверительной вероятностью δ₂ = 0.9; 0.95; 0.99, что средняя наработка на отказ T_О не ниже 500 часов, если m = 10.

Задачу решить, приняв допущение, что случайная величина T_О имеет экспоненциальный закон распределения и за период наблюдения отказы отсутствуют (n =0).

Методическое указание: для расчета использовать таблицы 1.1 и 2.2.а[6].

 

Задача 1.4.

Определить доверительные границы вероятности отказа изделий в интервале времени (0...8760) часов, если известно, что за 8760 часов наблюдения из m изделий отказало n. Заданная доверительная вероятность:

δ₂ = 0.9; 0,95; 0.99. Задачу решить с использованием таблицы 5.2 [6], которая содержит заранее вычисленные значения Q_В и Q_Н с точностью до трех десятичных знаков. Таблица 5.2 рассчитана до m <=500 и для δ₂ = 0.9; 0.95; 0.99.

Методическое указание: для вариантов задания использовать таблицу 1.2.

 

Задача 1.5.

За 8760 часов наработки изделий получена статистика по отказам:

Таблица 1.3 вариантов задания

Nп/п	m	n	Nп/п	m	n	Nп/п	m	n

 

С доверительной вероятностью δ₂ = 0.9, 0.95, 0.99 определить точечную и интервальную оценки вероятности отказа изделия за указанное время.

Методическое указание:

Задачу решить с использованием асимптотических формул для определения доверительных границ Q_В и Q_Н, в которые входят Q - процентные точки χ² - распределения с k = 2n или k=2n+1 степенями свободы, определяемые по таблице 2.2а [6].

Задача 1.6.

За время испытаний (0, t) не отказал ни один из 5, 10, 20 электродвигателей. Определить, какова их надежность, вычислив верхнюю доверительную границу вероятности отказа с заданными коэффициентами доверия δ₁ = 0.90, 0.95, 0.99.

 

 

По результатам, полученных решений задач сделать выводы о надежности изделий и дать рекомендации по использованию методов оценки вероятности безотказной работы изделий.

 

Вопросы к лабораторной работе № 1

1. Какие случайные события изучаются в теории надежности?

2. Перечислить случайные величины, соответствующие случайным событиям в теории надежности.

3. Что называется случайной величиной?

4. Классификация случайных величин. Привести примеры.

5. По какой информации получают наиболее достоверные оценки показателей надежности?

6. Что называется выборкой из генеральной совокупности?

7. Чем отличается выборка от генеральной совокупности?

8. Каким образом объем выборки влияет на анализ показателей надежности?

9. Что происходит при увеличении объема выборки с характеристиками надежности?

10. Точные (теоретические) характеристики случайных величин определяются: а) по выборке;

б) по генеральной совокупности.

11. Что необходимо знать для полной характеристики любой случайной

величины?

12. Какие показатели надежности могут быть членами вариационного ряда?

13. Что называется оценкой параметра надежности? Перечислите виды оценок показателей надежности?

14. Что является точечной оценкой?

15. Что является интервальной оценкой? Виды доверительных интервалов.

16. Почему интервал называется доверительным?

17. Что означает «точность количественного показателя надежности»?

18. Что называется достоверностью? Как обозначается?

19. Что называется уровнем значимости и как обозначается?

20. При каком условии применяются точные методы оценок показателей

надежности?

21. Когда применяются приближенные методы оценок показателей

надежности?

22. Может ли зависеть интервальная оценка показателей надежности от плана испытаний при прочих равных условиях? Если может, то привести пример.

23. При каких условиях вероятность отказа Q(t) определяется

биномиальным законом распределения?

24. Что называется «частотой» отказа, как обозначается и каким образом

определяется?

25. Каким соотношением связаны Т₀ и λ при допущении о простейшем

потоке отказов?

Лабораторная работа № 2

Метод статистических гипотез

Проверка гипотезы о законе распределения

 

Постановка задачи

Используя критерий Колмогорова, проверить, насколько справедливо предположение, что выборка интервалов времени безотказной работы изделий (таблица 2), полученная при их эксплуатации, случайна и взята из непрерывного распределения: Q(t) = 1 - exp(-t_б.р./T₀)

Сведения из теории

Общая характеристика метода. Статистической гипотезой называют всякое высказывание о генеральной совокупности, проводимое по выборке из этой совокупности. Статистические гипотезы классифицируют на гипотезы о законах распределения и гипотезы о параметрах законов распределения.

В общем виде задача проверки статистической гипотезы формулируется следующим образом. Имеем статистические данные в виде одной или нескольких выборок. Высказывается предположение о параметрах или законе распределения выборок. Это основное предположение называютнулевой гипотезой и обозначают H_О. Альтернативой исходной гипотезе H_О могут быть одна или две гипотезы H₁ и H₂. Таким образом, задача проверки гипотезы H_О для выборки, состоящей из n наблюдений Х₁,..., Х_n случайной величины X, заключается в выработке определенных правил, по которым решаем принять гипотезу H_О или H₁ (H₂). Все возможное множество выборок объема n можно разделить на два непересекающихся подмножества S_n1 и S_n2. Если наша выборка (или ее характеристики, параметры) попадают в область S_n1, то принимается исходная гипотеза H_О, если же в область S_n2, то нулевая гипотеза H_О отвергается и принимается гипотеза H₁ (H₂). Подмножество S_n1 называют областью допустимых значений случайной величины, а S_n2 - критической областью. Выбор одной из областей однозначно определяет и другую область. Возникает необходимость формирования критериев, принципов или правил для построения критической области S_n2 или области допустимых значений S_n1.

При выборе критической области и принятии или отклонении гипотезы H_О по случайной выборке принятое решение соответствует истине с некоторой доверительной вероятностью.

При выборе критической области, приняв или отклонив нулевую гипотезу H_О, можно допустить ошибки двух видов. Ошибка первого рода с вероятностью α состоит в том, что отвергается верная гипотеза H_О и принимается конкурирующая гипотеза H₁ (H₂), что символически можно записать в следующем виде: α = P{(x₁,..., x_n) Sn_n2 ‌ H₀}, то есть вероятность принятия гипотезы H₁ (H₂), когда на самом деле имеет место гипотеза H_О.

Ошибка второго рода с вероятностью β состоит в том, что принимается неверная гипотеза H_О, в то время как в действительности верна конкурирующая гипотеза H₁ (H₂), что символически записывается в виде:

β = P{(x₁,..., x_n) Sn_n1 ‌ H₁}, то есть вероятность принятия гипотезы H_О, когда на самом деле имеет место гипотеза H₁(H₂).

В технической литературе вероятность α иногда встречается под названием «риск» поставщика, а вероятность β - под названием «риск» заказчика.

Существуют различного рода статистические гипотезы: о сравнении двух вероятностей отказа; об однородности двух выборок; о законе распределения случайной величины.

 

Вопрос о сравнении двух вероятностей отказа постоянно возникает при сравнении надежности однотипного оборудования, работающего одновременно в различных условиях, или одного и того же оборудования, но за разные периоды эксплуатации. Часто требуется сравнить надежность оборудования, проработавшего одинаковое время.

 

Задача проверки однородности выборок может возникать уже на начальной стадии исследования надежности изделия с целью их объединения и получения более весомой выборки. Если гипотеза об однородности выборок подтверждается, следовательно, обе выборки извлечены из одной и той же генеральной совокупности, а расхождение статистических данных является случайным и несущественным. Для проверки исходной гипотезы предлагается использовать критерий Смирнова, согласно которому величина наибольшего абсолютного расхождения D_m,n сравнивается с критическим значением этой статистики D_m,n (α) при заданном уровне значимости α.

Если окажется, что D_m,n < D_m,n (α), то гипотеза об однородности двух выборок не бракуется, если же D_m,n ≥ D_m,n (α), то основную гипотезу Н_О отвергают в пользу альтернативной гипотезы Н₁.

 

Определение законов распределения случайных величин по эксплуатационной информации. Известно, что для полной характеристики любой случайной величины необходимо знать ее закон распределения в виде функции распределения (в нашем случае вероятности отказа) или плот­ности вероятности. Определение закона распределения отказов (восстановлений) по опытным данным, т.е. по выборке, осуществляется в 3 этапа:

1) выбор предполагаемого вида закона распределения;

2) проверка согласия выборки с принятым законом распределения, т.е. согласованности опытного распределения с теоретическ

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: