 |
Методические указания для выполнения контрольной работы
|
|
|
|
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
СТУДЕНТАМИ ЗАОЧНОГО ОТДЕЛЕНИЯ
При выполнении контрольных работ необходимо соблюдать следующие требования:
1. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки.
2. Каждую контрольную работу следует выполнять в отдельной тонкой тетради.
3. На обложке тетради должны быть ясно написаны название дисциплины; номер контрольной работы; фамилия, имя, отчество студента; шифр специальности и номер группы; номер зачетной книжки.
4. В начале работы должен быть указан номер варианта.
5. Перед выполнением каждого задания следует полностью привести его условие.
6. Каждое задание должно заканчиваться словом «Ответ» с приведением результата. Если это вычисление интеграла или производной или т.д., результат должен быть выделен подчеркиванием.
7. Выполнение заданий контрольной работы следует сопровождать краткими пояснениями.
8. В конце работы должна стоять личная подпись студента и дата выполнения контрольной работы.
Содержание контрольной работы
Задача 1.
1.1. Абонент забыл последнюю цифру номера телефона и потому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более чем в три места.
1.2. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса, содержащиеся в его экзаменационном билете; б) студент знает только два вопроса своего экзаменационного билета; в) студент знает только один вопрос своего экзаменационного билета.
1.3. Вероятность улучшения спортсменом личного достижения по прыжкам в длину равна 0,4. Чему равна вероятность того, что он улучшит свой результат, если ему предоставлена возможность прыгать три раза.
|
|
|
1.4. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складывают в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в 2 раза меньше, чем второго. Определить вероятность того, что взятая из ящика наудачу деталь будет бракованной.
1.5. В урне 10 белых и 5 черных шаров. Чему равна вероятность того, что, вынув наудачу с возвращением 6 шаров, получим белых не менее 3-х.
1.6. На факультете насчитывается 1460 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно пяти студентов.
1.7. Три стрелка в одинаковых независимых условиях произвели по одному выстрелу по одной и той же мишени. Вероятность поражения мишени первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадет в мишень; б) только два стрелка попадут в мишень; в) все три стрелка попадут в мишень.
1.8. В первой бригаде токарей 2 рабочих имеют первый разряд, 2 рабочих – второй, 5 рабочих – четвертый. Во второй бригаде 1 токарь имеет первый разряд, 4 токаря – третий, 2 токаря – четвертый. Из первой бригады во вторую переведен один токарь. Найти вероятность того, что рабочий, наудачу выбранный из нового состава второй бригады, имеет разряд не ниже второго.
1.9. В правом кармане имеется три монеты по 1 рублю и четыре монеты по 50 копеек, а в левом - шесть монет по 1 рублю и три монеты по 50 копеек. Из правого в левый карман наудачу перекладываются пять монет. Определить вероятность извлечения из левого кармана (после перекладывания) монеты в 1 рубль, если монета берется наудачу.
1.10. Вероятность нарушения работы кинескопа телевизора в течение гарантийного срока равна 0,12. Найти вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок.
|
|
|
Задача 2.
Дискретная случайная величина 
может принимать только два значения 
и 
, причем < . Известны вероятность 
возможного значения , математическое ожидание 
и дисперсия 
. Найти закон распределения этой случайной величины:
2.1. 
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 
2.7. 
2.8. 
2.9. 
2.10. 
Задача 3.
Случайная величина задана функцией распределения (интегральной функцией) 
. Найти плотность распределения вероятностей (дифференциальную функцию) 
, математическое ожидание и дисперсию . Построить графики интегральной и дифференциальной функций:
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 
3.6. 
3.7. 
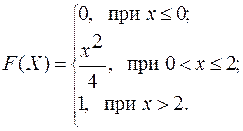3.8. 
3.9. 
3.10. 
Задача 4.
Известны математическое ожидание 
и среднее квадратическое отклонение 
нормально распределенной случайной величины . Найти вероятность попадания этой случайной величины в заданный интервал 
.
4.1. 
.
4.2. 
.
4.3. 
.
4.4. 
.
4.5. 
.
4.6. 
.
4.7. 
.
4.8. 
.
4.9. 
.
4.10.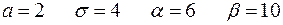 
.
Задача 5.
Из генеральной совокупности , распределенной по нормальному закону, извлечена выборка. Требуется:
1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
2. Построить полигон относительных частот;
3. Построить график эмпирической функции распределения;
4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
5. С надежностью 
найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
5.1. 
| 5,0 | 5,6 | 5,8 | 5,4 | 5,8 | 5,2 | 5,0 | 5,6 |
| 5,6 | 5,6 | 5,4 | 5,2 | 5,4 | 5,8 | 5,4 | 5,6 |
| 5,4 | 5,4 | 5,4 | 5,2 | 5,6 | 6,0 | 5,0 | 5,8 |
| 5,2 | 5,8 | 5,6 | 5,2 | 6,0 | 5,8 | 6,0 | 5,8 |
| 5,4 | 6,2 | 5,6 | 6,2 | 5,6 | 5,6 | 6,0 | 5,2 |
5.2. 
5.3.
| 7,6 | 7,8 | 7,4 | 7,8 | 7,2 | 7,6 | ||
| 7,6 | 7,6 | 7,4 | 7,2 | 7,4 | 7,8 | 7,4 | 7,6 |
| 7,4 | 7,4 | 7,4 | 7,2 | 7,6 | 7,8 | ||
| 7,2 | 7,8 | 7,6 | 7,2 | 7,8 | 7,8 | ||
| 7,4 | 8,2 | 7,6 | 8,2 | 7,6 | 7,6 | 7,2 |
5.4.
| 13,1 | 11,1 | 12,1 | 9,1 | 12,2 | 12,1 | 10,1 | 12,1 |
| 15,1 | 11,1 | 13,1 | 14,1 | 13,1 | 11,1 | 11,1 | 12,1 |
| 13,1 | 11,1 | 12,1 | 11,1 | 10,1 | 14,1 | 12,1 | 10,1 |
| 9,1 | 10,1 | 12,1 | 15,1 | 9,1 | 13,1 | 11,1 | 13,1 |
| 12,1 | 12,1 | 14,1 | 11,1 | 10,1 | 14,1 | 12,2 | 12,1 |
|
|
|
5.5.
| 11,7 | 12,3 | 11,1 | 10,8 | 11,4 | 11,1 | 11,1 | 11,4 |
| 11,4 | 11,4 | 11,7 | 11,1 | 12,3 | 11,1 | 10,5 | |
| 10,8 | 10,5 | 10,8 | 11,1 | 11,7 | 11,7 | ||
| 11,4 | 11,1 | 11,4 | 11,4 | 11,4 | 10,8 | 11,4 | |
| 10,5 | 11,7 | 11,4 | 11,4 | 11,7 | 11,4 | 11,4 | 10,8 |
5.6.
| 11,6 | 11,8 | 11,4 | 11,8 | 11,2 | 11,6 | ||
| 11,6 | 11,6 | 11,4 | 11,2 | 11,4 | 11,8 | 11,4 | 11,6 |
| 11,4 | 11,4 | 11,4 | 11,2 | 11,6 | 11,8 | ||
| 11,2 | 11,8 | 11,6 | 11,2 | 11,8 | 11,8 | ||
| 11,4 | 12,2 | 11,6 | 12,2 | 11,6 | 11,6 | 11,2 |
5.7.
| 12,5 | 10,5 | 11,5 | 8,5 | 11,5 | 11,5 | 9,5 | 11,5 |
| 14,5 | 10,5 | 12,5 | 13,5 | 12,5 | 10,5 | 10,5 | 11,5 |
| 12,5 | 10,5 | 11,5 | 10,5 | 9,5 | 13,5 | 11,5 | 9,5 |
| 8,5 | 9,5 | 11,5 | 14,5 | 8,5 | 12,5 | 10,5 | 12,5 |
| 11,5 | 11,5 | 13,5 | 10,5 | 9,5 | 13,5 | 11,5 | 11,5 |
5.8.
| 12,7 | 13,3 | 12,1 | 11,8 | 12,4 | 12,1 | 12,1 | 12,4 |
| 12,4 | 12,4 | 12,7 | 12,1 | 13,3 | 12,1 | 11,5 | |
| 11,8 | 11,5 | 11,8 | 12,1 | 12,7 | 12,7 | ||
| 12,4 | 12,1 | 12,4 | 12,4 | 12,4 | 11,8 | 12,4 | |
| 11,5 | 12,7 | 12,4 | 12,4 | 12,7 | 12,4 | 12,4 | 11,8 |
5.9.
| 13,6 | 13,8 | 13,4 | 13,8 | 13,2 | 13,6 | ||
| 13,6 | 13,6 | 13,4 | 13,2 | 13,4 | 13,8 | 13,4 | 13,6 |
| 13,4 | 13,4 | 13,4 | 13,2 | 13,6 | 13,8 | ||
| 13,2 | 13,8 | 13,6 | 13,2 | 13,8 | 13,8 | ||
| 13,4 | 14,2 | 13,6 | 14,2 | 13,6 | 13,6 | 13,2 |
5.10.
Задача 6.
Для выборки, извлеченной из генеральной совокупности и представленной интервальным рядом (в первой строке указаны интервалы значений 
исследуемого количественного признака генеральной совокупности; во второй – частоты 
, т.е. количество элементов выборки, значения 
признака которых принадлежат указанному интервалу). Требуется:
1) Построить полигон относительных накопленных частот (кумулятивную кривую);
2) Построить гистограмму частот и гистограмму относительных частот;
3) Найти выборочную среднюю, выборочную дисперсию, моду и медиану;
4) Проверить на уровне значимости 
гипотезу о нормальном распределении признака генеральной совокупности по критерию согласия Пирсона;
5) В случае согласованности с нормальным распределением найти с надежностью доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака генеральной совокупности.
|
|
|
6.1.
|
| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
|
|
6.2.
|
| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
|
|
6.3.
|
| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
|
|
6.4.
|
| 10-12 | 12-14 | 14-16 | 16-18 | 18-20 | 20-22 | 22-24 |
|
|
6.5.
|
| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
|
|
6.6.
|
| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
|
|
6.7.
|
| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
|
|
6.8.
|
| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
|
|
6.9.
|
| 0,6-0,95 | 0,95-1,30 | 1,30-1,65 | 1,65-2,00 | 2,00-2,35 | 2,35-2,70 | 2,70-3,05 |
|
|
6.10.
|
| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
|
|
Замечание: При отыскании выборочной средней и выборочной дисперсии в задачах 5 и 6 для упрощения счета рекомендуется переходить к условным вариантам.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
1. Классический способ подсчета вероятностей
Определение: Событие называется случайным по отношению к данному испытанию, если при осуществлении этого испытания оно может произойти или не произойти.
Классическое определение вероятности. Если испытание сводится к полной группе равновозможных несовместных событий (классическая схема), то вероятность события А в данном испытании равна отношению числа элементарных исходов благоприятствующих появлению этого события к общему числу элементарных исходов испытания.
Вероятность события обозначают через Р (А). По определению
0≤Р(А)≤1 (1)
В формуле (1) m – число всех исходов благоприятствующих появлению событий А, n – общее число исходов испытания.
Задача 1. Брошен наудачу шестигранный игральный кубик. Найти: 1) вероятность появления цифры три на верхней грани игральной кости, 2) вероятность появления четного числа очков.
Решение: Испытание состоит в бросании игрального кубика. Всего шесть элементарных исходов испытания: выпадение цифры 1, 2, 3, 4, 5, 6. Эти исходы являются: несовместными, так как никакие два не произойдут одновременно; равновозможными, так как бросают кубик наудачу (никакой из исходов не имеет предпочтений в появлении перед остальными); перечисленные шесть исходов образуют полную группу событий, так как в результате испытания произойдет хотя бы один из них. Таким образом, имеет место классическая схема.
1. Пусть событие А – появление цифры три на верхней грани кубика. Вероятность этого события можно вычислить по формуле (1), где m = 1, а п=6. Следовательно, Р (А) = 
.
|
|
|
2. Событие В – появление четного числа очков на верхней грани кубика. Вероятность этого события вычислим по той же формуле (1), где m = 3, так как событию благоприятствуют исходы: появление цифры 2, цифры 4, цифры 6, а n=6. Следовательно Р(В)= 
= 
.
Задача 2. В группе 25 студентов. Из них по контрольной работе 20 студентов получили хорошие и удовлетворительные оценки, остальные не справились с предложенной работой. Какова вероятность того, что два студента, вызванных к доске, имеют неудовлетворительные оценки по контрольной работе.
Решение: Имеет место классическая схема. Испытание состоит в выборе двух студентов из 25 человек. Общее число возможных элементарных исходов испытания равно числу способов выбора из 25 человек двух студентов. В комбинациях из 25 человек по два важен состав, но безразличен порядок. Такие комбинации в комбинаторике называются сочетаниями и их число можно подсчитать по формуле числа сочетаний из n элементов по m:
(2)
Где n=25, m = 2 и, следовательно, С225= 
= 
= 
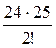=300.
Пусть событие А – два вызванных к доске студента имеют неудовлетворительные оценки. Вероятность этого события подсчитаем по формуле (1). Общее число элементарных исходов испытания подсчитано выше, а число элементарных исходов благоприятствующих появлению события А – число способов выбрать двух студентов имеющих неудовлетворительные оценки из общего числа студентов несправившихся с контрольной работой. Число таких комбинаций подсчитаем по формуле (2), где n=25-20=5, а m=2.
= 
= 
= 
=10. Итак, Р(А)= 
= 
.
|
|
|
