 |
Интегрирование по параметру
|
|
|
|
Глава 7
Собственные интегралы (Римана), зависящие от параметра
Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике
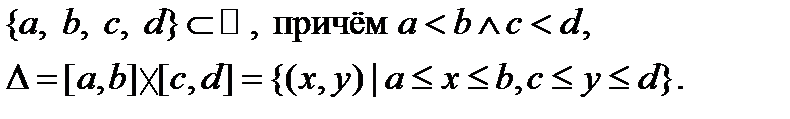
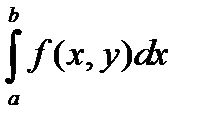
 Если для любого существует интеграл, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):
Если для любого существует интеграл, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):
Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра, т.е. определяемые т.о. функции часто используют в математических рассуждениях и приложениях.
Следует иметь ввиду, что

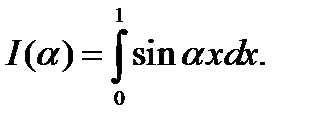 Пример 1. Рассмотрим функцию
Пример 1. Рассмотрим функцию
В этом примере интеграл легко вычислить:
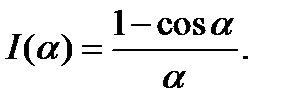
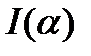
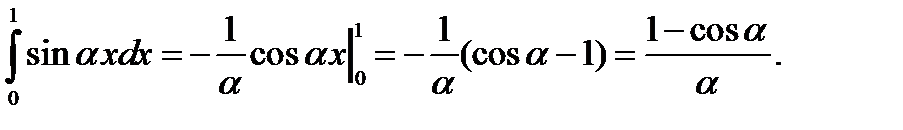
Значит, можно задать и обычным способом:
Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.
Возможна и более сложная ситуация, когда от параметра зависит не только подынтегральная функция, но и пределы интегрирования:
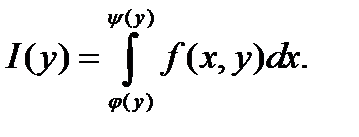
Основные теоремы
Предельный переход под знаком интеграла
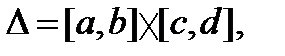 Теорема 1 ( о непрерывности интеграла с параметром ).
Теорема 1 ( о непрерывности интеграла с параметром ).
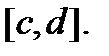
 Если функция f(x,y) непрерывна на прямоугольнике то
Если функция f(x,y) непрерывна на прямоугольнике то
функция непрерывна на отрезке
 Доказательство. По теореме Кантора, непрерывная на компактном множестве ∆ функция является равномерно непрерывной, т.е.
Доказательство. По теореме Кантора, непрерывная на компактном множестве ∆ функция является равномерно непрерывной, т.е.
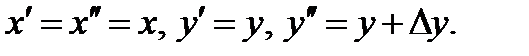
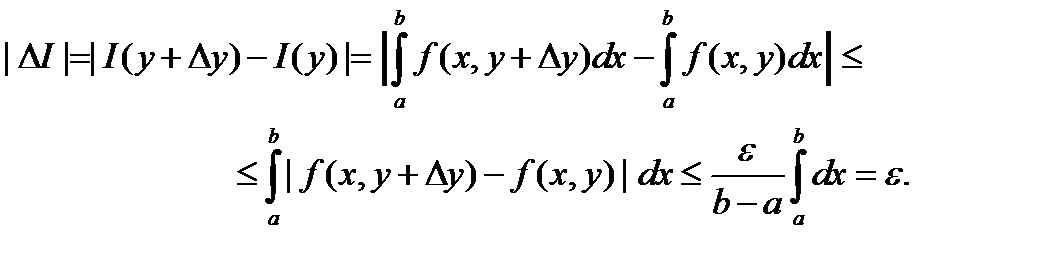
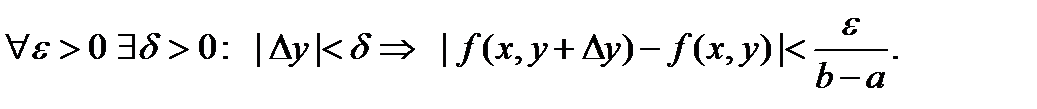 Возьмём Тогда из равномерной непрерывности следует:
Возьмём Тогда из равномерной непрерывности следует:
Оценим теперь приращение функции I (y):
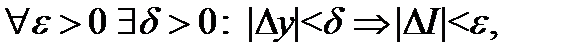
Итак, что и означает непрерывность функции I (y).
Замечание. В теореме 1 требуется, чтобы f (x,y) была непрерывной по обеим переменным в совокупности, т.е. чтобы
|
|
|
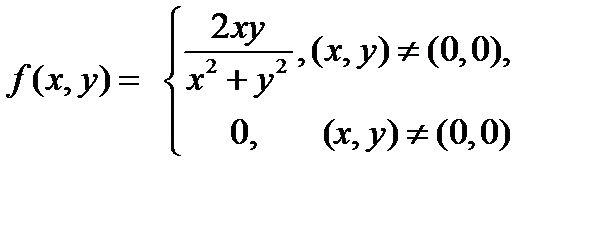 Недостаточно, чтобы f (x,y) была непрерывной по каждой из переменных. Например, функция
Недостаточно, чтобы f (x,y) была непрерывной по каждой из переменных. Например, функция
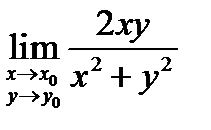 непрерывна по x (при любом фиксированном y), и непрерывна по y (при любом фиксированном x). Однако она не является непрерывной в точке (0,0) функцией (по совокупности переменных): предел не
непрерывна по x (при любом фиксированном y), и непрерывна по y (при любом фиксированном x). Однако она не является непрерывной в точке (0,0) функцией (по совокупности переменных): предел не
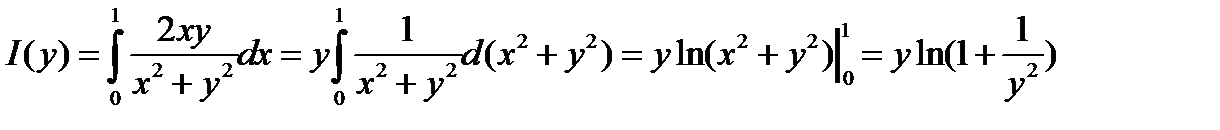 существует. В данном случае не справедлив и вывод теоремы 1; например, функция
существует. В данном случае не справедлив и вывод теоремы 1; например, функция
разрывна в точке y = 0.
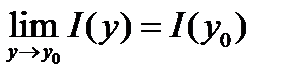 Так как непрерывность в точке I (y) означает, по определению, что
Так как непрерывность в точке I (y) означает, по определению, что
в любой точке y 0, то непосредственно из теоремы 1
вытекает
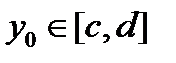
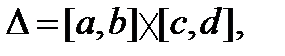 Теорема 2 ( о предельном переходе под знаком интеграла ).
Теорема 2 ( о предельном переходе под знаком интеграла ).
Если f (x,y) непрерывна на то для любого
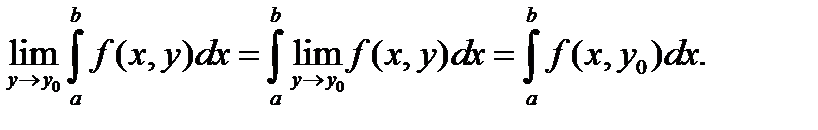
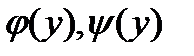 Если – непрерывные функции, а f (x, y) непрерывна на множестве
Если – непрерывные функции, а f (x, y) непрерывна на множестве
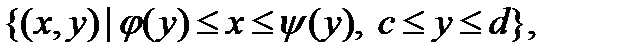
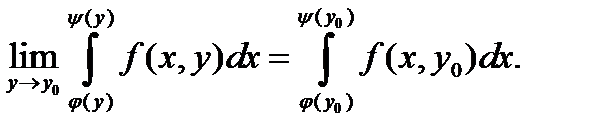 то можно доказать, что
то можно доказать, что
Это утверждение усиливает теоремы 1 и 2.
Ещё одно усиление теорем 1,2 связано с заменой требования непрерывности f (x, y) более слабым условием.
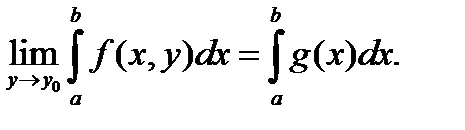 Теорема 3. Если f (x, y) непрерывна по x (при любом фиксированном y) и f (x, y) равномерно сходится к функции g (x) при y → y 0, то
Теорема 3. Если f (x, y) непрерывна по x (при любом фиксированном y) и f (x, y) равномерно сходится к функции g (x) при y → y 0, то
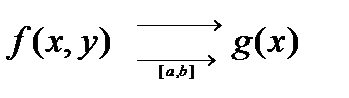
Равномерная сходимость: означает:
Доказательство. просто – оно проводится с помощью той же оценки, что и доказательство теоремы 1.
Теорема 3 справедлива также в случае y → ∞, лишь определение равномерной сходимости имеет другой вид:
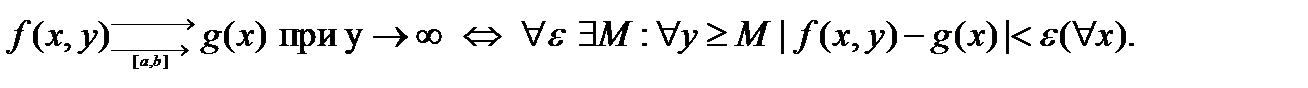
 Пример 2. Вычислить.
Пример 2. Вычислить.
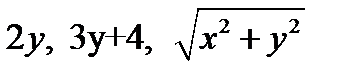
Решение. Так как функция непрерывны при любых
x, y, то возможен предельный переход под знаком интеграла:

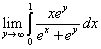
Пример 3. Вычислить.
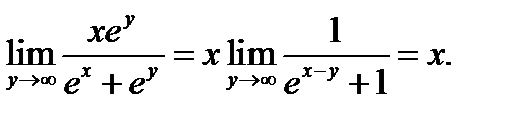 Решение. Подынтегральная функция непрерывна при любых x, y и y →∞ стремится к g (x)= x:
Решение. Подынтегральная функция непрерывна при любых x, y и y →∞ стремится к g (x)= x:
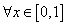
Эта система равномерная, так как

,
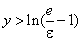
если только. Значит, возможен переход к пределу под
знаком интеграла:
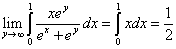
.
Дифференцирование по параметру
Дифференцируемость интеграла зависящего от параметра (Правило Лейбница)
Пусть для интеграла 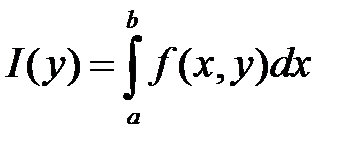 , в котором подынтегральная функция зависит от некоторого параметра «у» будет меняться, то будет меняться и значение определенного интеграла.
, в котором подынтегральная функция зависит от некоторого параметра «у» будет меняться, то будет меняться и значение определенного интеграла.
|
|
|
Т.о. определенный интеграл есть функция от «у» поэтому мы его можем обозначить через 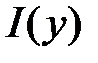
Теорема 4. Предположим, что 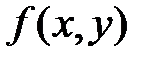 и
и 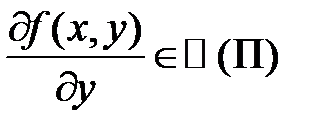 ,
,
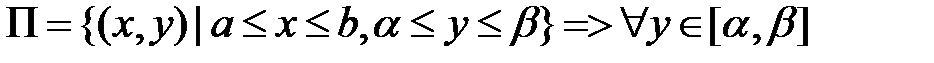
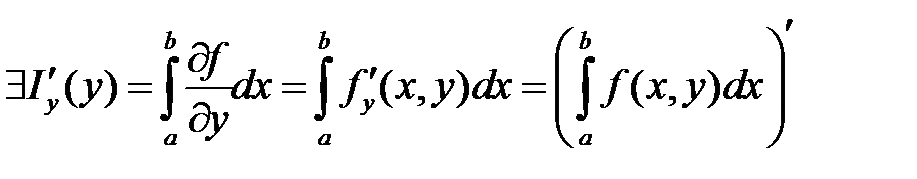
Доказательство
Найдем производную интеграла по параметру «у». Для  и приращение
и приращение  таких, что
таких, что
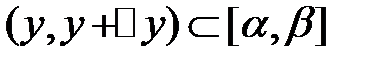 . Тогда производная
. Тогда производная 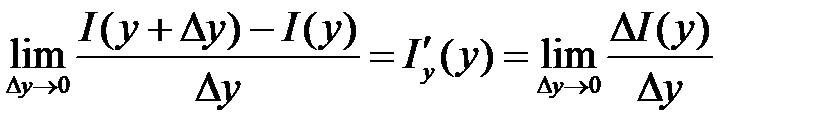
Заметим, что 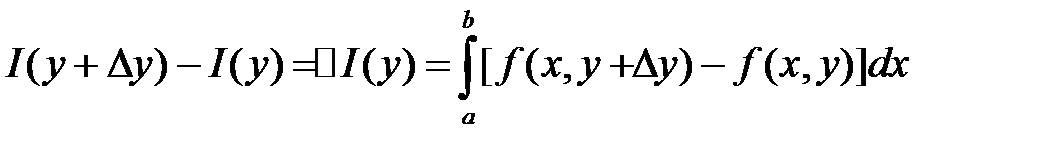
Поделим обе части последнего равенства на «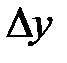 »
»
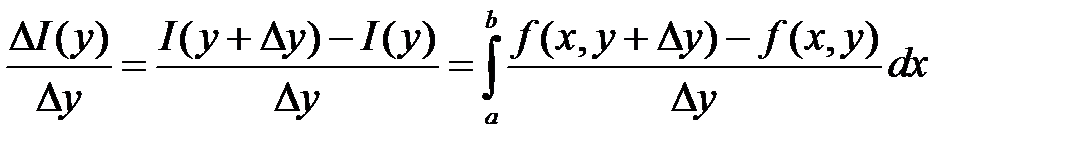
Применяя теорему Лагранжа к подынтегральной функции, будем иметь:
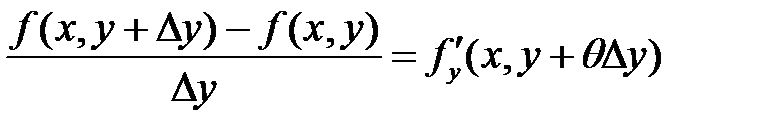 , где
, где 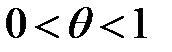
Т.к.
Осталось доказать, что можно перейти к пределу под знаком интеграла. Чтобы воспользоваться теоремой 3, докажем, что 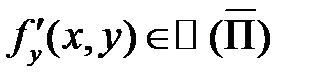 (
( - замкнутая область)
- замкнутая область)
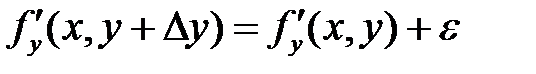 , где
, где  зависит от
зависит от 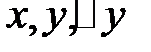 стремится к нулю при
стремится к нулю при 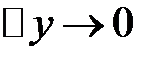
Т.о. 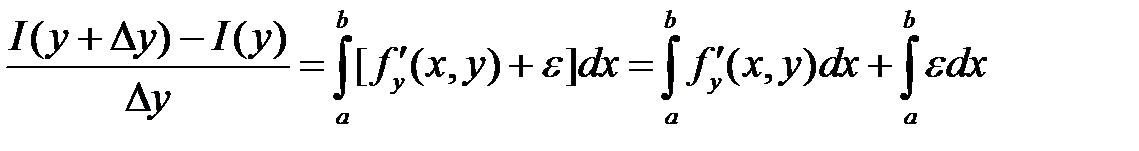
Переходя к пределу при 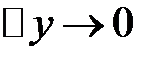 получаем:
получаем:
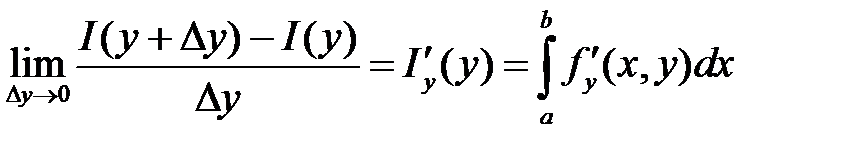
Или 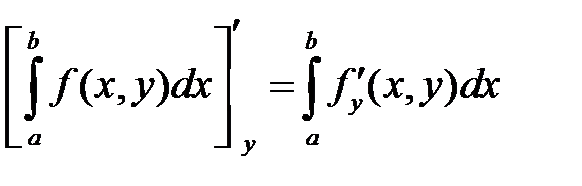
Эта формула называется формулой Лейбница.
(Замечание: Подынтегральная функция в интеграле 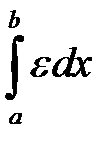 стремится к нулю при
стремится к нулю при  . Из того, что подынтегральная функция в каждой (.) стремится к нулю, не всегда следует, что интеграл также стремится к нулю. Однако в данном случае
. Из того, что подынтегральная функция в каждой (.) стремится к нулю, не всегда следует, что интеграл также стремится к нулю. Однако в данном случае  при
при 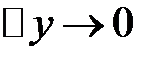 . Этот факт мы принимаем без доказательства.)
. Этот факт мы принимаем без доказательства.)
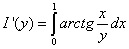
Пример 4. Найти производную функции в точке y = 2.
 Решение. Можно, вычислив интеграл, найти явное выражение для функции I (y), а затем продифференцировать. Проще, однако, применить теорему 4:
Решение. Можно, вычислив интеграл, найти явное выражение для функции I (y), а затем продифференцировать. Проще, однако, применить теорему 4:
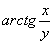
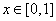
При и значениях y, близких к 2, функция и её частная
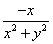
производная, очевидно, непрерывны.
Пример 5. Вычислить
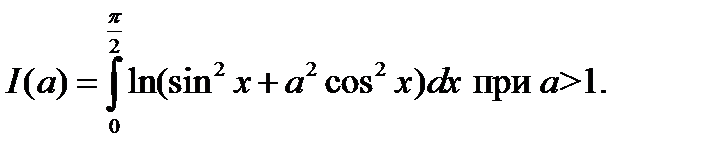

 Решение. Найдём производную интеграла по параметру. Легко проверить, что требования теоремы 4 соблюдены, поэтому
Решение. Найдём производную интеграла по параметру. Легко проверить, что требования теоремы 4 соблюдены, поэтому
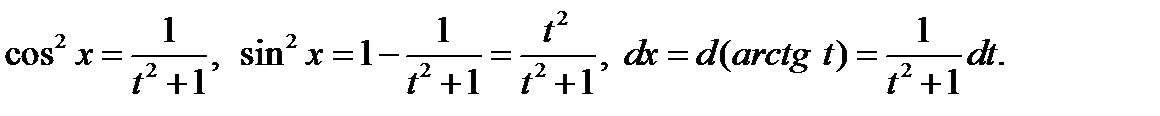
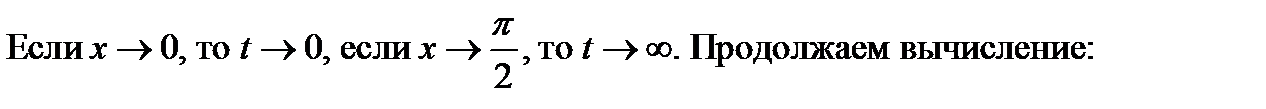 Применим подстановку t = tg x. Тогда
Применим подстановку t = tg x. Тогда
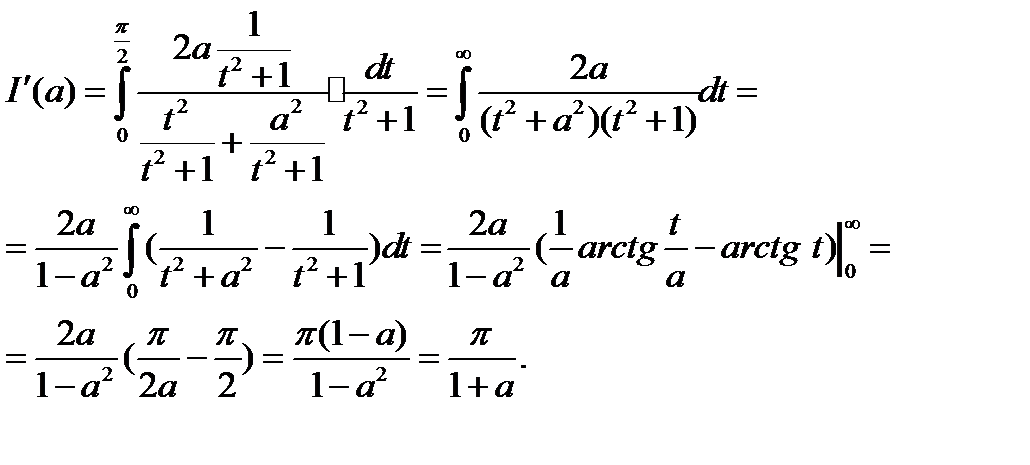
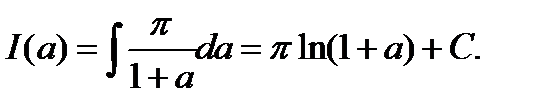 Теперь, вычисляя интеграл, получим:
Теперь, вычисляя интеграл, получим:
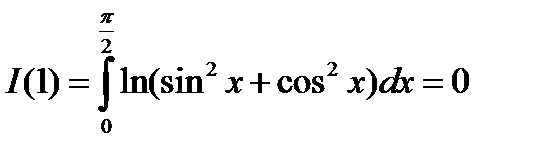 Константу C найти легко, так как
Константу C найти легко, так как
.

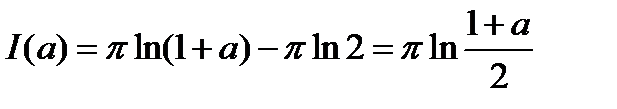
.
Научимся теперь вычислять производные в случае, если от параметра зависит не только подынтегральная функция, но и пределы интегрирования.
Теорема 5.

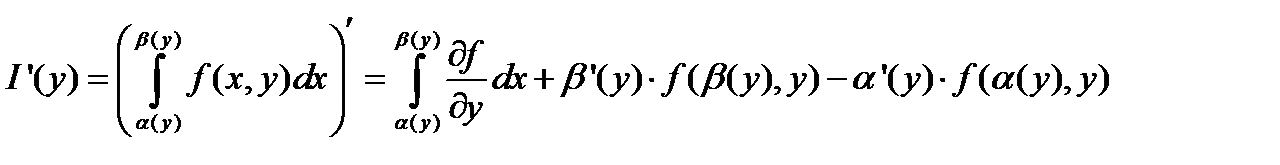
Доказательство. Возьмём произвольную точку и воспользуемся аддитивностью интеграла:
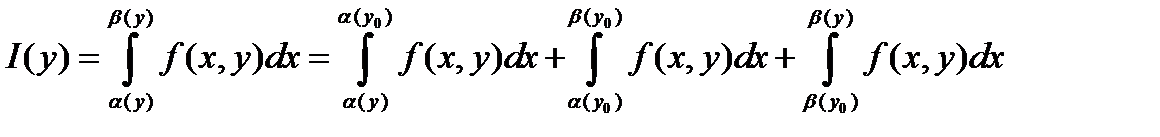
Найдём производную 3-го слагаемого по определению:
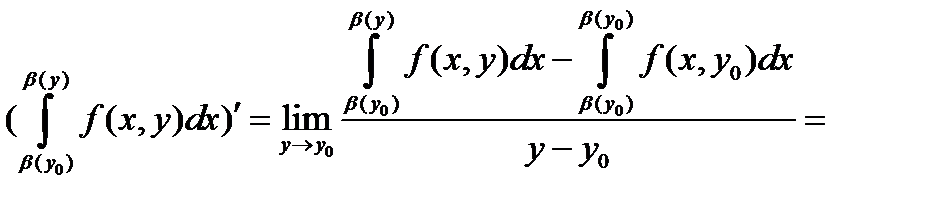
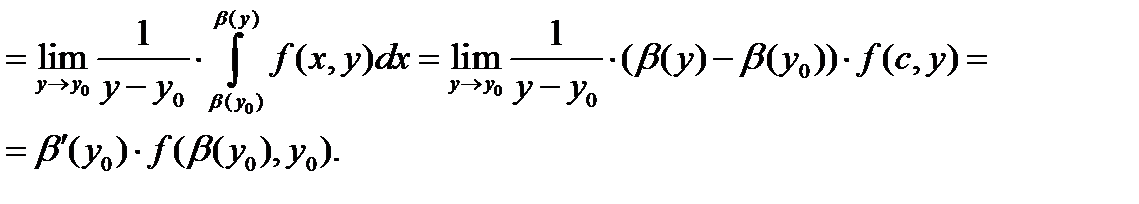
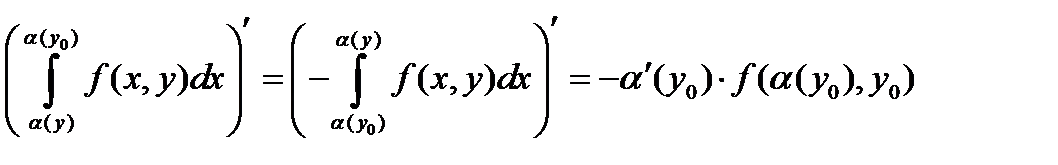 Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f (x, y) и дифференцируемостью β (y). В точности так же вычисляется и производная 1-го слагаемого:
Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f (x, y) и дифференцируемостью β (y). В точности так же вычисляется и производная 1-го слагаемого:
.
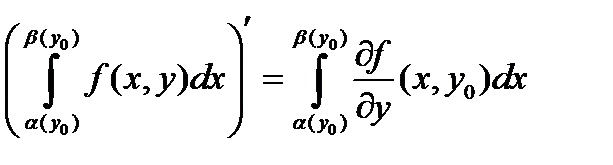 Производная 2-го слагаемого вычисляется по теореме 4:
Производная 2-го слагаемого вычисляется по теореме 4:
|
|
|
.
Складывая все 3 слагаемые, получим требуемую формулу.
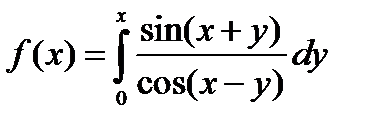
Пример 6. Найти производную функции.
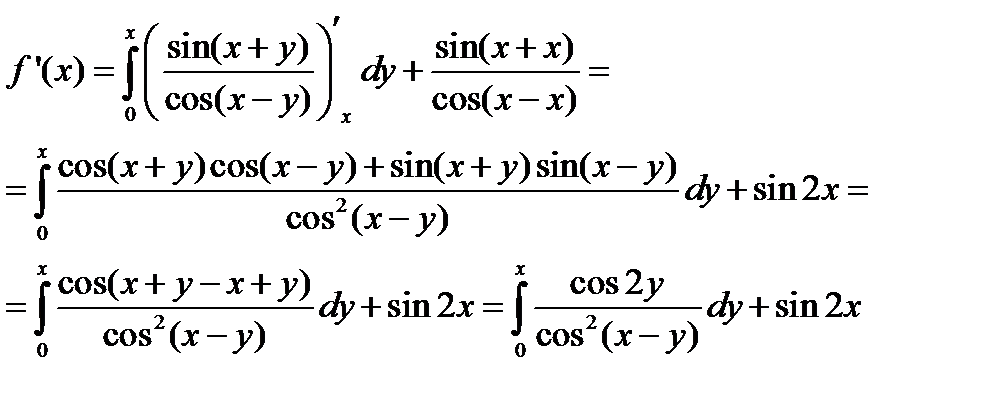 Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5:
Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5:
.
Интегрирование по параметру
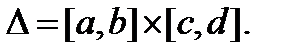 Теорема 7. Пусть функция f (x, y) непрерывна в прямоугольнике
Теорема 7. Пусть функция f (x, y) непрерывна в прямоугольнике
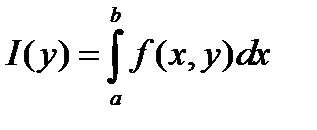
Рассмотрим. Тогда
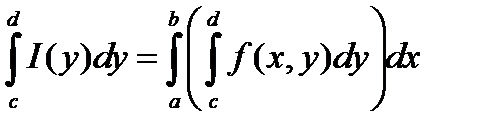
.
Или, что то же самое,
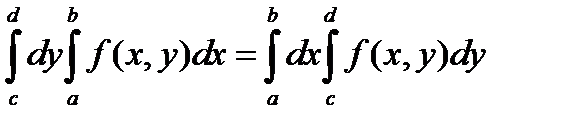
.
Доказательство. Докажем более общее соотношение. Пусть t – произвольная точка отрезка [ c, d ]. Докажем, что
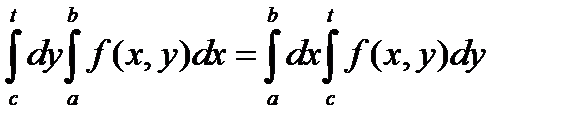
. (*)
 Найдем производную по t от каждой части этого равенства. Применяя теорему 5 (иди давно известную нам теорему об интеграле с переменным верхним пределом), получим:
Найдем производную по t от каждой части этого равенства. Применяя теорему 5 (иди давно известную нам теорему об интеграле с переменным верхним пределом), получим:
В правой части равенства (*) – интеграл, зависящий от параметра t. Дифференцируем его, применяя теорему 4:
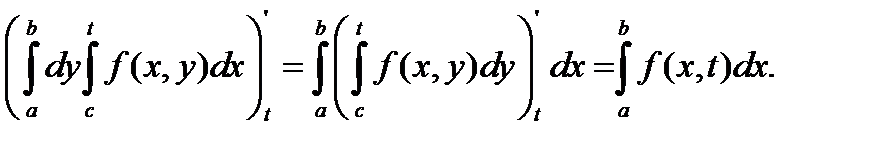
Одинаковые результаты говорят о том, что функции в левой и правой частях равенства (*) отличаются лишь на константу:
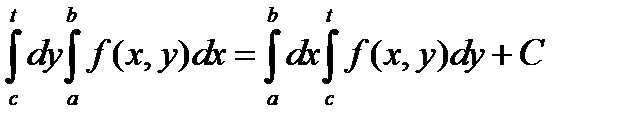
.
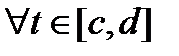
Это верно. В частности, при t = c получим: 0 = 0 + C, т.е.
С = 0, и равенство доказано. Если применить его при t = d, получим утверждение теоремы.
Теорема 7’. Пусть 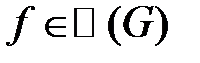
Тогда 
Доказательство
Заметим, что если 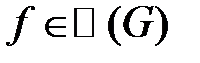 , тогда
, тогда 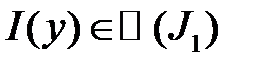 интеграл в скобках – непрерывная функция на
интеграл в скобках – непрерывная функция на  . Поэтому все интегралы в утверждении теоремы определены.
. Поэтому все интегралы в утверждении теоремы определены.
Для каждого 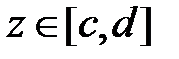 положим
положим 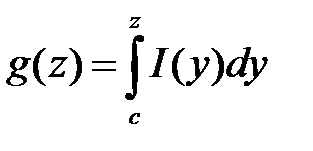 ,
, 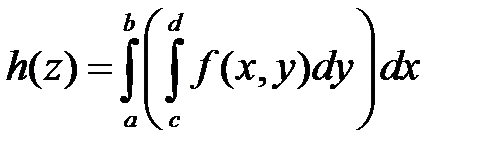 .
.
Поскольку 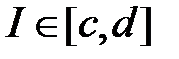 то
то 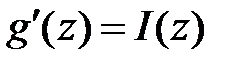 ,
, 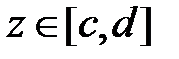 . Функция
. Функция 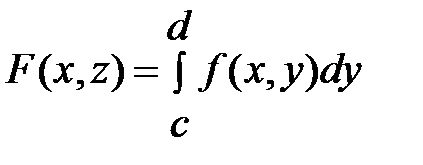 ,
,
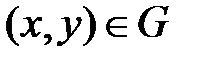 при
при 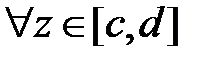 непрерывна по «х» на
непрерывна по «х» на 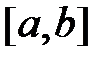 , согласно теоремы 3 (о непрерывности I(y))
, согласно теоремы 3 (о непрерывности I(y))
Для любой точки 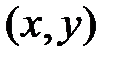
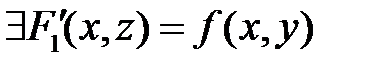 и
и 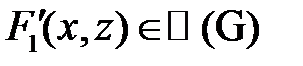 . Поэтому согласно теоремы 4, для
. Поэтому согласно теоремы 4, для 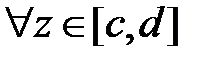
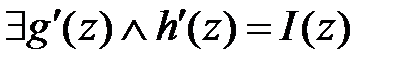 . Т.о.
. Т.о. 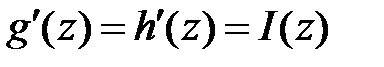 ,
, 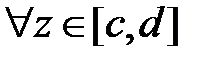 . Причем
. Причем 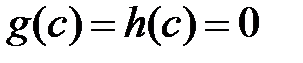 . Следовательно
. Следовательно 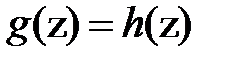
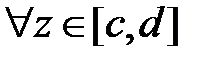 .
.
Доказываемое равенство получим при 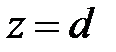 .
.
Пример 7. Вычислить интеграл
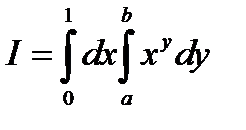
Решение. Интегрирование в указанном порядке затруднительно:
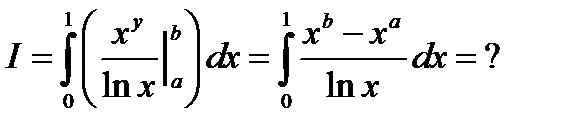
Пользуясь теоремой 6, изменим порядок интегрирования.
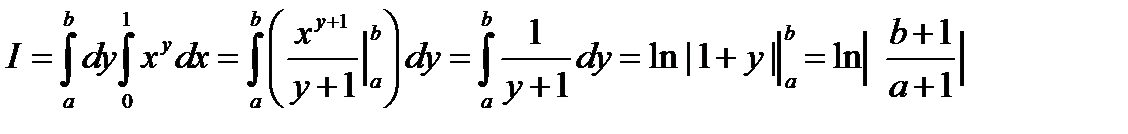
.
Интеграл вычислен. Попутно получено соотношение:
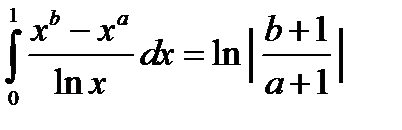
.
Приведём пример, показывающий, что при нарушении непрерывности подинтегральной функции изменение порядка интегрирования может привести к другому результату.
Пример 8. Вычислим интеграл:
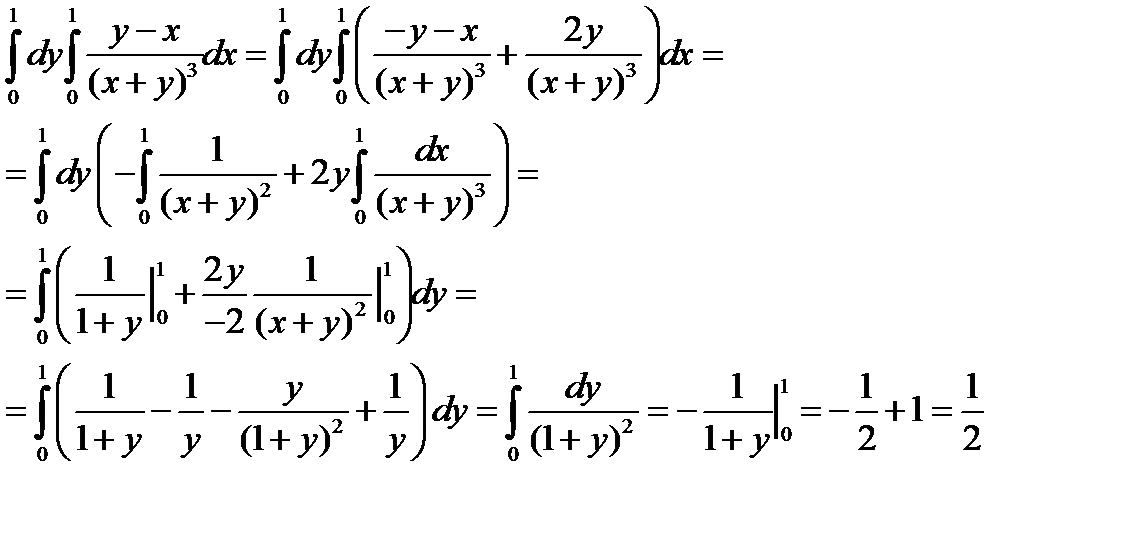
.
При вычислении в другом порядке можно заметить, что если сменить знак подинтегральной функции, то получится уже рассмотренный интеграл:
|
|
|

|
|
|


