 |
Энергетические характеристики сигналов
|
|
|
|
Варианты заданий
| № | 1 сигнал | 2 сигнал | |
| 1. | Единичный импульс
 , τ = 2c , τ = 2c
| Последовательность прямоугольных импульсов с амплитудой А =2, длительностью t =0.3с и периодом повторения Т =1с | |
| 2. | Единичный скачок
 , τ = -1.5c , τ = -1.5c
| Полигармонический сигнал
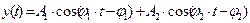 ,
A1 = 2, ω1 = 1, φ1 = 0
A1 = 3, ω2 = 5, φ2 = 2 ,
A1 = 2, ω1 = 1, φ1 = 0
A1 = 3, ω2 = 5, φ2 = 2
| |
| 3. | Функция Гаусса
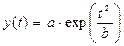 , a = 10, b = 5 , a = 10, b = 5
| Сигнал вида 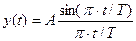 ,
амплитуда A = 1, период T = 1c (полупериод) ,
амплитуда A = 1, период T = 1c (полупериод)
| |
| 4. | Односторонний экспоненциальный импульс  , а = 4, b = 2 в интервале [0, 0.2] , а = 4, b = 2 в интервале [0, 0.2]
| Последовательность треугольных импульсов с периодом повторения Т=1 и амплитудой A = 1 | |
| 5. | Функция Лапласа
 , а = 8, b = 5, τ = 0.1c в интервале [-0.2, 0.2] , а = 8, b = 5, τ = 0.1c в интервале [-0.2, 0.2]
| Пилообразный сигнал с периодом повторения Т =2с и амплитудой A = 1 | |
| 6. | Гармонический сигнал
 , A = 5, ω = 2, φ = 1 , A = 5, ω = 2, φ = 1
| Меандр с амплитудой А =2 и периодом повторения Т =0,5 с | |
| 7. | Полигармонический сигнал
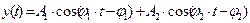 ,
A1 = 5, ω1 = 2, φ1 = 1
A1 = 2, ω2 = 3, φ2 = 2 ,
A1 = 5, ω1 = 2, φ1 = 1
A1 = 2, ω2 = 3, φ2 = 2
| Прямоугольный импульс с амплитудой А =2, длительностью импульса t =1.5с | |
| 8. | Последовательность прямоугольных импульсов с А =5, длительностью t =0.2с и периодом повторения Т =1с | Прямоугольный импульс с амплитудой А =0.5, длительностью импульса t =0.6с и задержанный во времени на 0.3с | |
| 9. | Меандр с амплитудой А =3 и периодом повторения Т =1 с | Несимметричный треугольный импульс
 , амплитуда A = 5, период T = 1c , амплитуда A = 5, период T = 1c
| |
| Пилообразный сигнал с периодом повторения Т =1с и амплитудой A = 2 | Полигармонический сигнал
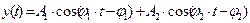 ,
A1 = 2, ω1 = 1, φ1 = 6
A1 = 0.5, ω2 = 3, φ2 = 0 ,
A1 = 2, ω1 = 1, φ1 = 6
A1 = 0.5, ω2 = 3, φ2 = 0
|
Примечания:
- При выполнении курсовой работы можно использовать средства любых программных комплексов, таких как MATLAB, Mathcad, Maple и др.
- Номер варианта выбирается по последней цифре учебного шифра (если последняя цифра 0, то выбирается задание № 10).
- Рекомендуемый учебник: Сергиенко А.Б. Цифровая обработка сигналов.
Теоретические сведения:
|
|
|
Сигналы и их характеристики
Сигналом называется некоторое волновое явление. Сигнал, несущий в себе некоторую информацию и только её, называется полезным сигналом. Сигнал, не несущий в себе никакой полезной информации, называется шумом или помехой. Обычно сигнал, поступающий на обработку, представляет собой суперпозицию, то есть сумму, полезного сигнала и шума, такой сигнал называется зашумленным сигналом.
Физическая природа сигнала может быть весьма различной. Очень часто это электрическое напряжение, несколько реже – ток, возможны и др. физические величины.
С математической точки зрения сигнал представляет зависимость одной величины от другой. Чаще всего это зависимость от времени.
Классификация сигналов
Различают детерминированные (его значение в любой момент времени можно определить точно) и случайные сигналы (случайная величина с некоторой вероятностью)
Следующий важный класс сигналов – сигналы с интегрируемым квадратом  или сигналы с ограниченной энергией.
или сигналы с ограниченной энергией.
Еще один признак классификации сигналов, существенно влияющий на методы их анализа, - периодичность. Для периодического сигнала 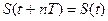 при любом t, (n – произвольное число, T – период). Любой периодический сигнал имеет бесконечную энергию.
при любом t, (n – произвольное число, T – период). Любой периодический сигнал имеет бесконечную энергию.
Следующий класс – сигналы конечной длительности (финитные сигналы). Они отличны от нуля, но только на ограниченном промежутке времени.
Перейдем к более узким, так называемым тестовым сигналам, применяющимся для анализа сигналов и систем:
1) гармонические колебания  , А – амплитуда, ω – частота, φ – начальная фаза. Применяется для анализа характеристик цепей.
, А – амплитуда, ω – частота, φ – начальная фаза. Применяется для анализа характеристик цепей.
Есть еще 2 важные в радиотехнике функции, тоже относящиеся к тестовым:
2) дельта-функция, или функция Дирака  - бесконечный узкий импульс с бесконечной амплитудой, расположенной при «нулевом» значении аргумента функции.
- бесконечный узкий импульс с бесконечной амплитудой, расположенной при «нулевом» значении аргумента функции.
|
|
|

Sимпульса =1,  . Сигнал
. Сигнал  невозможно реализовать физически.
невозможно реализовать физически.  важен для теоретического анализа сигналов и систем. На графиках изображается жирной стрелкой, высота которой пропорциональна множителю, стоящему перед дельта-функцией. Одно из важных свойств
важен для теоретического анализа сигналов и систем. На графиках изображается жирной стрелкой, высота которой пропорциональна множителю, стоящему перед дельта-функцией. Одно из важных свойств  – фильтрующее свойство: если
– фильтрующее свойство: если  присутствует под интегралом в качестве множителя, то результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредочен дельта-импульс.
присутствует под интегралом в качестве множителя, то результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредочен дельта-импульс.
3) функция единичного скачка  , или функция Хевисайда, или функция включения. Она равна нулю
, или функция Хевисайда, или функция включения. Она равна нулю  для отрицательных значений аргумента и равна
для отрицательных значений аргумента и равна  для положительных. При нуле функцию считают либо неопределенной, либо равной ½. Эту функцию удобно использовать при создании математических выражений для сигналов конечной длительности. (С помощью
для положительных. При нуле функцию считают либо неопределенной, либо равной ½. Эту функцию удобно использовать при создании математических выражений для сигналов конечной длительности. (С помощью  можно любую кусочно-заданную зависимость записать в виде единого математического выражения).
можно любую кусочно-заданную зависимость записать в виде единого математического выражения).
Основной целью анализа сигналов является сравнение сигналов друг с другом для выявления их сходства и различия. Можно выделить 3 основных составляющих анализа сигналов:
- измерение числовых параметров сигналов; к ним относятся энергия, средняя мощность и среднеквадратичное значение;
- разложение сигнала на элементарные составляющие; такое разложение производится с использованием ряда Фурье и преобразования Фурье;
- количественное измерение степени «похожести» различных сигналов(корреляционный анализ).
Энергетические характеристики сигналов
Одной из составляющих анализа сигналов является измерение их количественных параметров: 1) энергии; 2) средней мощности (за заданный промежуток времени) 3) мгновенной мощности.
Их определения, принятые в теории сигналов, отличаются от обычных.
Обычные «физические» понятия мощности и энергии: если к резистору с сопротивлением R приложено напряжение U, то мощность равна  ; энергия
; энергия  за время T.
за время T.
Пусть к этому резистору приложен сигнал S(t). Мощность, рассеивающаяся в резисторе, будет зависеть от времени t, т.е. речь идет о мгновенной мощности:
 .
.
Чтобы вычислить выделяющуюся за t энергию, p(t) нужно проинтегрировать:

|
|
|
Среднюю мощность за заданный промежуток времени t получим, разделив энергию на длительность временного интервала:

Энергия и мощность интересуют нас с точки зрения сравнения различных сигналов. Поэтому исключим сопротивление нагрузки(R = 1). И тогда получим формулы для энергии, мгновенной мощности и средней мощности, принятые в теории сигналов:


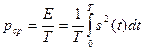
Мощность имеет размерность В2, а энергия – В2с.
Корреляционный анализ
Суть корреляционного анализа состоит в количественном измерении степени сходства различных сигналов. Для этого служат корреляционные функции.
Корреляционная функция
Корреляционная функция детерминированного сигнала с конечной энергией представляет собой интеграл от произведения двух копий сигнала, сдвинутых друг относительно друга на время  :
:

Корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией – чем больше значение корреляционной функции, тем это сходство сильнее. Кроме того, корреляционная функция обладает следующими свойствами:
1. Значение КФ при  =0 равно энергии сигнала, то есть интегралу от его квадрата
=0 равно энергии сигнала, то есть интегралу от его квадрата

2. КФ является четной функцией своего аргумента  :
:

3. Значение КФ при  =0 является максимально возможным значением:
=0 является максимально возможным значением:

4. С ростом абсолютного значения  КФ сигнала с конечной энергией затухает:
КФ сигнала с конечной энергией затухает:
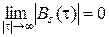
5. Если сигнал s(t) не содержит особенностей в виде дельта-функций, его КФ не может иметь разрывов (то есть обязана быть непрерывной функцией).
6. Размерность КФ сигнала – B2/с, если сигнал - напряжение.
В случае периодического сигнала (и вообще любого сигнала с бесконечной энергией) воспользоваться приведенным определением не удастся. КФ периодического сигнала с периодом Т вычисляют, усредняя произведение сдвинутых копий в пределах одного периода:

Набор свойств такой КФ несколько меняется:
1. Значение КФ при  =0 равно не энергии, а средней мощности анализируемого сигнала
=0 равно не энергии, а средней мощности анализируемого сигнала

2. Свойство четности сохраняется

3. Значение КФ при  =0 по-прежнему является максимально возможным значением:
=0 по-прежнему является максимально возможным значением:
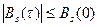
4. КФ периодического сигнала является периодической функцией с тем же периодом, что и сам сигнал:
|
|
|

5. Если сигнал не содержит дельта-функций, его КФ будет непрерывной функцией.
6. Размерность КФ периодического сигнала – квадрат размерности сигнала (B2, если сигнал - напряжение).
|
|
|


