 |
Темы проектных и исследовательских работ
|
|
|
|
Лабораторная работа №9.
Тема: «Проблема вычисление площадей криволинейных фигур. Определенный интеграл»
Вводная беседа
Давайте вспомним, как развивались наши знания о методах вычисления площадей планиметрических фигур. В начальной школе мы изготавливали из целлофана особый измерительный инструмент – «Палетку» (рисунок 86). Она помогала нам определять примерное значение площади фигуры подсчетом количества квадратов единичной площади (рисунок 87- 88).
Рисунок 86 Рисунок 87 Рисунок 88
В тот период форма самой фигуры нам была неважна, от нее зависела лишь точность измерения, а не сама возможность применения метода.
Затем, мы получили формулы для вычисления площади квадрата (
) и прямоугольника 
, сначала с целочисленными измерениями, а затем и произвольными.
К применению этих формул и к следствиям из них мы стали сводить любые задачи на вычисление площадей многоугольных фигур. Для этого мы разрезали фигуры на подходящие части и складывали из них прямоугольник или квадрат. Примерами равносоставленных фигур являются: на рисунке 89 - треугольник и прямоугольник, на рисунке 90 - параллелограмм и прямоугольник, а на рисунке 91 - трапеция и прямоугольник.
Рисунок 89 Рисунок 90 Рисунок 91
Этот метод в истории математики называется методом квадратур (поскольку задача сводилась первоначально к поиску способа замены многоугольника равновеликим ему квадратом).
Применение этого метода опиралось на теорему планиметрии о том, что все равносоставленные фигуры равновелики.
Знание формулы площади треугольника мы использовали для того, чтобы получить формулы площадей правильных многоугольников вписанных в окружность данного радиуса и описанных около ее. На рисунке 92 представлена триангуляция правильных многоугольников и формулы в общем виде.
|
|
|
Рисунок 92
Поскольку любая многоугольная фигура триангулируема, т.е. может быть представлена в виде объединения треугольников, то вопрос о способе вычисления площадей многоугольников оказался, таким образом, закрыт.
В курсе геометрии мы лишь однажды получали формулу площади криволинейной фигуры. Это был круг. Для вычисления его площади мы уже пользовались методами математического анализа: предельным переходом и методом исчерпывания.
При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к границе круга - окружности.
Рисунок 94
Площадь круга – это предельное значение площадей правильных вписанных и описанных многоугольников при неограниченном увеличении числа их сторон. Поскольку обе площади имеют общий предел, их разность стремится к нулю, значит, круг – квадрируемая фигура, т.е. имеет площадь и её значение можно найти по формуле: 
(рисунок 95).
Рисунок 95 Рисунок 96
Сегодня нам предстоит использовать весь накопленный нами опыт сведения вопроса о вычислении площади незнакомой фигуры к знакомым для получения формулы площади криволинейной трапеции (см. компендиум и рисунок 96), а затем и любой другой криволинейной фигуры, которая может быть представлена как объединение криволинейных трапеций.
Цель работы: вычисление площадей криволинейных фигур.
Оборудование: компьютер с установленной программой GeoGebra.
Компендиум
1. Равновеликие фигуры – это плоские (пространственные) фигуры, имеющие равные площади (объёмы).
2. Равносоставленные фигуры –это фигуры, которые можно разрезать на одинаковое число соответственно равных частей.
3. Теорема. Любые две равносоставленные плоские фигуры равновелики.
4. Квадрирование – разрезание фигуры на возможно меньшее число частей, из которых затем можно сложить квадрат.
|
|
|
5. Криволинейная трапеция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции 
, определенной на отрезке [a; b], осью абсцисс, прямыми 
и 
6. Квадратура — (лат. quadratura, придание квадратной формы) — математический термин, первоначально обозначавший нахождение площади заданной фигуры или поверхности; построение с помощью циркуля и линейки квадрата, равновеликого данной фигуре; вычисление интеграла (неопределённого или определённого).
7. Определенный интеграл –это предел интегральных сумм 
.
Ход работы:
Предлагаем открыть файл вGeoGebra и выполнить приведенную ниже серию заданий.
Задание 1. Постройте криволинейную трапецию заданную уравнением 
на отрезке 
. Предложите способ построения равновеликого ей прямоугольника. Используя этот способ, вычислите площадь данной криволинейной трапеции.
Шаг 1. Постройте фрагмент графика функции на отрезке .
Шаг 2. Проведите прямые 
; 
.
Нарисуйте эскиз криволинейной трапеции.
Гипотеза oспособе преобразования в равновеликий прямоугольник:____________________________________________
Шаг 3. Проверьте свою гипотезу, выполнив построенияв GeoGebra. Нарисуйте эскиз получившегося прямоугольника.
Шаг 3. Найдите площадь этого прямоугольника. Докажите, что он равновелик данной криволинейной трапеции по построению.
Доказательство: _______________________________________
Задание 2. Пользуясь строкой ввода постройте фрагмент графика любой известной вам функции на отрезке [2;7]. Постройте криволинейную трапецию, заданную этим фрагментом. Подбирая подходящие точки на криволинейной части, замените криволинейную трапецию фигурой, состоящей из прямоугольников (ступенчатой фигурой). Используя эту ступенчатую фигуру, найдите приближенное значение площади криволинейной трапеции. Нарисуйте эскиз всех построений.
Опишите способ замены криволинейной трапеции, заданной функцией 
на отрезке [a;b], ступенчатой фигуры, примерно равной площади. Запишите саму приближенную формулу площади. Сравните ее с определением определенного интеграла. Сделайте вывод.
Вывод
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
|
|
Задание 3. Проверьте правильность своих выводов, вычислением интеграла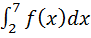 
. Для расчетов используйте инструмент «интеграл». Сравните результаты вычислений площади ступенчатой фигуры и интеграла.
Вывод _______________________________________________
____________________________________________________
Заключительная беседа
Численное интегрирование (историческое название численная квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Численное интегрирование уравнений движения планет, комет и искусственных небесных тел во многих случаях осуществляется с помощью метода численного интегрирования, получившего в теоретической астрономии названиеметода квадратур. Этот метод представляет интерес и для инженеров-вычислителей, особенно при решении задач, требующих большой точности.
Сегодня эти поиски представляют собой отдельную математическую задачу, решением которой занимаются ученые с использованием компьютерных средств, в том числе GeoGebra.
Темы проектных и исследовательских работ
1. Метод квадратур при интегрировании в школе
2. Применение сумм Дарбу
3. Задачи, разрешимые в квадратурах
4. Простейшие квадратурные формулы
5. Интегрирование иррациональных функций
|
|
|
