 |
Определение и свойства основных геометрических фигур.
|
|
|
|
Пятый постулат. Открытие геометрий, отличных от Евклида.
Для построения геометрии достаточно выбрать лишь несколько положений, взяв их непосредственно из практики, и с помощью логических рассуждений получить остальные необходимые рассуждения. Положения следует называть аксиомами, следствия из них теоремами. Древнегреческий геометр Евклид Александрийский является автором труда «Начала», в котором перечисляются аксиомы – положения, их 5:
- Через две точки можно провести прямую.
- Прямую можно продолжить в обе стороны.
- Около любой точки произвольным радиусом можно провести окружность.
- Все прямые углы равны между собой.
- Если две прямые на плоскости в пересечении с третьей образуют внутренние односторонние углы, сумма которых меньше двух прямых углов, то эти прямые пересекаются (Другая формулировка: в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной).
ФОРМУЛИРОВКА V ПОСТУЛАТА
Вот о чем говорится в пятом постулате:
Если две прямые а и в образуют при пересечении с третьей прямой внутренние односторонние углы a и в, сумма величин которых меньше двух прямых углов (т.е. меньше 180°; рис. 1), то эти две прямые обязательно пересекаются, причем именно с той стороны от третьей прямой, по которую расположены углы а и в (составляющие вместе менее 180°).
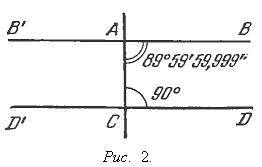
Последний пятый постулат обратил на себя особое внимание, поскольку формулировался значительно сложнее и не был интуитивно понятен как остальные. Проблема V постулата была впервые решена профессором Казанского университета, гениальным русским математиком Николаем Ивановичем Лобачевским (1792-1856), открывшим в 1862 г. первую неевклидову геометрию, называемую так же «гиперболической».
|
|
|
Совокупность теорем геометрии, не зависящих от евклидовой аксиомы параллельности, венгерский математик Янош Бойяи назвал «абсолютной» геометрией. Все же остальные теоремы, то есть те, при доказательстве которых мы непосредственно или косвенно основываемся на V постулате, составляет собственно евклидову геометрию.
Среди неевклидовых геометрий можно выделить следующие:
- Геометрия Лобачевского, Гаусса, Бойяи. В плоскости через точку А вне прямой а можно провести более 1 прямой, параллельной данной.
- Сферическая геометрия. Геометрия на поверхности сферы, основные факты которой были изучены еще в древности, в связи с задачами астрономии. Дело в том, что поверхность Земли представляет собой практически правильную сферу, поэтому необходима была геометрия, обеспечивающая правильность расчетов в условиях искривленных поверхностей.
- Геометрия Римана. Основывалась на сферической геометрии. Риман существенно расширил список теорем и аксиом. Геометрия Римана — одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана — реализуется на поверхностях с постоянной положительной гауссовой кривизной. В геометрии Римана прямая определяется двумя точками, плоскость — тремя, две плоскости пересекаются по прямой и т. д., но через данную точку нельзя провести к прямой ни одной параллельной. В частности, в этой геометрии имеется теорема: сумма углов треугольника больше двух прямых. Исторически геометрия Римана появилась позже двух других геометрий (в 1854 г.).Геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. Поэтому иногда геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены; таким образом из сферы получается проективная плоскость.
Особая роль V постулата, его большая сложность и меньшая наглядность (по сравнению с другими аксиомами) привели к тому, что математики позднейших веков стали пытаться доказать этот постулат как теорему. Некоторые из них старались вывести этот постулат из остальных аксиом Евклида, не добавляя к ним новых утверждений; другие же открыто заменяли V постулат иной аксиомой, которую они считали более простой и наглядной. Разумеется, новая аксиома содержала утверждение, равносильное V постулату. Но и анализ тех доказательств, в которых V постулат не заменялся другой аксиомой открыто, показывает, что здесь также использовались утверждения, равносильные V постулату, однако это делалось неявно, незаметно для автора доказательства.
|
|
|
Значение пятого постулата невозможно переоценить, так как без него не обошлась бы ни одна из двух известных нам геометрий. Если бы пятый постулат не рассмотрели ученые, то не было бы такого величайшего открытия, ведь с помощью неевклидовой геометрии люди получили новое представление о пространстве. Именно с пятого постулата все началось: он - точка отсчета, двигатель науки.
Интуиция подсказывала, что и евклидова и неевклидова геометрии являются примерами полноценной математики.
Определение и свойства основных геометрических фигур.
Основные свойства
1.Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
2.Отношение площадей треугольников, имеющих общие высоты, равно отношению оснований, соответствующих этим высотам.
3. Отношение площадей треугольников, имеющих общие основания, равно отношению высот, соответствующих этим сторонам треугольника.
4.В подобных треугольниках пропорциональны сходственные элементы, радиусы вписанных и описанных окружностей, периметры треугольников, квадратные корни из площадей.
5.Радиус вписанной окружности можно найти по формуле:
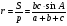
6.Радиус описанной окружности удобно находить с помощью теоремы синусов и косинусов:
|
|
|

7.Каждая медиана делит треугольник на 2 равновеликих треугольника.
8.Три медианы делят треугольник на 6 равновеликих треугольников.
9.Точка пересечения биссектрис делит биссектрису в отношении:
сумма сторон, образующих угол, из которого проведена биссектриса, к третьей стороне.
10.Медианы треугольника и стороны связаны формулой:

11.Прямая, параллельная стороне треугольника и пересекающая две другие, отсекает от него треугольник, подобный данному.
12. Если биссектрисы углов B и С треугольника ABC пересекаются в точке М, то 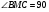
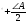 .
.
13. Угол между биссектрисами смежных углов равен 90 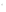 .
.
14. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то 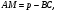 где
где  - полупериметр треугольника.
- полупериметр треугольника.
15. Окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС. Тогда расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
16. Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L и M. Если 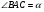 , то
, то  .
.
17. Теорема Менелая. Дан треугольник АВС. Некоторая прямая пересекает его стороны АВ, ВС и продолжение стороны АС в точках С1, А1,В1 соответственно. Тогда 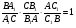
18. Теорема Чевы. Пусть точки А1,В1 и С1 принадлежат соответственно сторонам ВС, АС и АВ треугольника АВС. Отрезки АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда 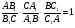
19. Теорема Штейнера-Лемуса. Если две биссектрисы треугольника равны, то он равнобедренный.
20. Теорема Стюарта. Точка D расположена на стороне ВС треугольника АВС, тогда 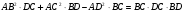 .
.
21.Внеписанной окружностью называют окружность, касающуюся одной из его сторон и продолжений двух других.
22.Для каждого треугольника существуют три внеписанных окружности, которые расположены вне треугольника.
23.Центром внеписанной окружности является точка пересечения биссектрис внешних углов треугольника и биссектрисы внутреннего, не смежного с этими двумя внешними.
24.Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС. Тогда расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
|
|
|
Задачи на построение.
|
|
|


