Главная | Обратная связь | Поможем написать вашу работу!

Приложения теории автоматов

Теория автоматов

Основные понятия

Объектомисследования теории автоматов являются различные преобразователи дискретной информации; она возникла в начале 50-х гг. 20 в. в связи с требованиями практики проектирования вычислительных машин и с разработкой математических моделей процессов переработки информации в технических, биологических, экономических и других системах.

Основными понятиями теории автоматов. являются понятия абстрактного автомата и понятие композиции автоматов. Эти понятия являются абстракциями реально существующих дискретных устройств — автоматов. Понятие абстрактного автомата позволяет характеризовать устройство с точки зрения алгоритма его функционирования, т. е. алгоритма переработки информации, который оно реализует. Понятие композиции автоматов позволяет характеризовать устройство с точки зрения его структуры, иными словами, даёт представление, каким образом данное устройство построено из других, более элементарных.

Автоматом называется дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы. Если множество состояний автомата, а так же множества входных и выходных сигналов конечны, то автомат называется конечным автоматом.

Понятие состояния введено в связи с тем, что часто возникает необходимость в описании поведения систем, выходные сигналы которых зависят не только от состояния входов в данный момент времени, но и от некоторых предысторий, т.е. от сигналов, которые поступали на входы системы ранее.

Информацию, поступающую на вход автомата, а так же выходную информацию принято кодировать конечной совокупностью символов. Эту совокупность называют алфавитом, отдельные символы, образующие алфавит – буквами, а любые упорядоченные последовательности букв данного алфавита – словами в этом алфавите.

Например. В алфавите X = (x₁, x₂), состоящем из двух букв, словами будут: x₁, x₂, x₁x₁, x₁x₂, x₂x₁,x₂x₂, x₁x₁x₁, и т.д.

Наряду со словами, состоящими не менее чем из одной буквы, введем слово, не содержащее ни одной буквы, которую будем обозначать символом е и называть пустым словом или пустой буквой.

Математической моделью реального конечного автомата является абстрактный автомат, который имеет один входной канал и один выходной канал.

A(a₀,a₁,a_n)

X y(y₁,y₂,…,y_k)

Рисунок 15.1

Автомат функционирует в дискретные моменты времени, интервал между которыми Т называется тактом. При этом в каждый дискретный момент времени на вход автомата поступает одна буква входного алфавита, автомат переходит из одного состояния в другое и выдается одна буква выходного алфавита. В зависимости от того, как задается длительность такта Т, различают автоматы синхронного действия (T = const) и асинхронного действия (T ¹ const). Мы будем рассматривать, в основном, синхронные автоматы, функционирующие в дискретные моменты времени, которые можно обозначить целыми не отрицательными натуральными числами, t=0,1,2,3,…., имеющими смысл номера такта.

Для задания конечного автомата S необходимо задавать совокупность из пяти объектов:

S(A, X, Y, d, l), (15.1)

где A = {a₀,a₁,a₂,...,a_n} – множество внутренних состояний автомата;

X = {x₁, x₂,…, x_m} – множество входных сигналов (входной алфавит);

X_iбуква входного алфавита;

Y = {y₁, y₂,…, y_k} – множество выходных сигналов (выходной алфавит);

d - функция переходов, определяющая состояние автомата a(t+1), в котором автомат будет находиться в момент времени (t+1), в зависимости от состояния автомата a(t) и входного сигнала x(t) в момент времени t, т.е. a(t+1) = d [a(t),x(t)];

l - функция выходов, определяющая значение выходного сигнала y(t) в зависимости от состояния автомата a(t) и входного сигнала x(t) в момент времени t, т.е. y(t) = l[a(t), x(t)].

Автомат работает следующим образом: в каждый момент времени t он находится в определенном состоянии a(t) из множества А возможных состояний, причем в начальный момент времени t = 0, он всегда находится в состоянии a(t = 0) = a₀. В момент времени t автомат воспринимает входной сигнал x(t), выдает выходной сигнал y(t) = l[a(t), x(t)] и переходит в следующее состояние a(t+1) = d[a(t), x(t)]. Другими словами, абстрактный автомат каждой паре символов a(t) и x(t) ставит в однозначное соответствие пару символов a(t+1) и y(t). Такие автоматы называют детерминированными. Преобразование информации в детерминированных автоматах подчиняется следующим условиям:

1. Любое входное слово длиною l букв, преобразуется в выходное слово той же длины.

2. Если каждый раз перед подачей входных сигналов автомат находится в одном и том же состоянии, то при совпадении в двух входных словах первых l1 букв, в выходных словах первые l1 букв тоже совпадут.

Кроме детерминированных автоматов существуют вероятностные или стохастические автоматы, в которых переход из одного состояния в другое под воздействием случайных или детерминированных входных сигналов происходит случайно. Работа таких автоматов описывается уже матрицей переходов d, элементами которой являются вероятности переходов из одного состояния в другое.

Применяемые на практике автоматы принято разделять на два класса: - это автоматы Мили и автоматы Мура, названные так по имени американских ученых, которые впервые начали их изучать.

Закон функционирования автоматов Мили описывается следующей системой уравнений:

a(t + 1) = d[a(t),x(t)] ü

y(t) = l[a(t),x(t)] ý. (15.2)

t = 0,1,2,3… þ

Работа автоматов Мура задается следующими уравнениями:

a(t + 1) = d[a(t),x(t)] ü

ý. (15.3)

y(t) = l[a(t)] þ

Отличительной особенностью автоматов Мили является то, что их выходные сигналы зависят как от состояния автомата, так и от значения входного сигнала. В автоматах Мура выходные сигналы y(t) в каждый дискретный момент времени t однозначно определяются состоянием автомата в тот же момент времени и не зависят от значения входного сигнала.

1. Графический способ задания автомата (задание автомата с помощью графа).

Этот способ основан на использовании ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги – переходам между ними. Две вершины графа a_i и a_s соединяются дугой, направленной от a_i к a_s, если в автомате имеется переход из a_i в a_s, т.е. a_s= d(a_i, x_j). В автомате Мили дуга отмечается входным сигналом x_j, вызвавшим переход, и выходным сигналом y_g, который возникает при переходе. Внутри кружочка, обозначающего вершину графа, записывается состояние. Например, для автомата Мили, приведенного выше, граф имеет вид с рис.12а), а для автомата Мура вид с рис 12б).

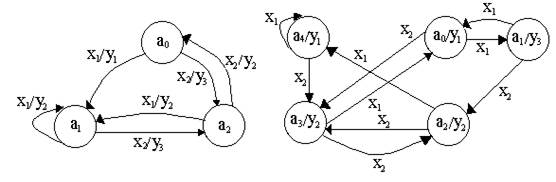
а) б)

Рисунок 12.2

В инженерной практике часто встречаются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются. Такие последовательности будем называть запрещенными входными словами данного автомата, а сам автомат – частичным автоматом. У частичного автомата функции переходов и выходов определены не на всех парах a_i, x_j. На месте неопределенных состояний и выходных сигналов ставится прочерк. При синтезе обычно производят доопределение частичного автомата, чтобы его схемная реализация получилась как можно проще.

x_j\a_i	a₀	a₁	a₂	a₃
x₁	a₁/y₁	a₃/y₃	a₂/y₂	a₂/y₁
x₂	- / -	- / -	a₀/y₄	a₀/y₂

Приложения теории автоматов

Теория автоматов находит применение, как в других областях математики, так и в решении практических задач. Например, средствами теории автоматов доказывается разрешимость некоторых формальных исчислений. Применение методов и понятий теории автоматов к изучению формальных и естественных языков привело к возникновению математической лингвистики (математическая лингвистика - математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков.) Понятие автомата может служить модельным объектом в самых разнообразных задачах, благодаря чему возможно применение теории автоматов в различных научных и прикладных исследованиях.

Основные приложения теория автоматов имеет в практике проектирования и автоматизации проектирования дискретных устройств и, в частности, вычислительных машин. Она приобретает всё более важное значение для таких классических математических дисциплин, как теория алгоритмов, с одной стороны, и таких современных теорий в математике и кибернетике, как теория формальных систем, теория программирования, теория формальных языков и грамматик — с другой.

Комбинаторика

Предмет и задачи

Предмету комбинаторики не так просто дать краткое исчерпывающее определение. В некотором смысле слово «комбинаторика» можно понимать как синоним термина «дискретная математика», то есть исследование дискретных конечных математических структур.

С точки зрения теории множеств комбинаторика изучает подмножества конечных множеств, их объединения и пересечения, а также различные способы упорядочивания этих подмножеств. Одной из общих задач комбинаторики является следующая:

1. Найти конфигурацию элементов, обладающую заранее заданными свойствами.

В некоторых случаях такую конфигурацию удается найти сразу, Например, если требуется расположить 10 точек и 5 отрезков так, чтобы на каждом отрезке было по 4 точки, то после недолгих размышлений мы вспоминаем фигуру пятиконечной звезды и располагаем наши элементы так, как показано на рисунке.

12 Следующая ⇒

Воспользуйтесь поиском по сайту: