Определение рациональных способов раскроя материала.

В задачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Пред­положим, что из единицы материала можно изготовить заготов­ки нескольких видов. Способ раскроя единицы материала назы­вается рациональным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.

Пусть k — индекс вида заготовки, k = 1,.... q; i — индекс спо­соба раскроя единицы материала, i = 1,..., р; а_ik — количество (це­лое число) заготовок вида k, полученных при раскрое единицы материала <-м способом.

Приведенное определение рационального способа раскроя мо­жет быть формализовано следующим образом.

Способ раскроя v называется рациональным (оптимальным по Па­рето), если для любого другого способа раскроя i из соотношений а_ik ³ а_vk, k = 1,..., q, следуют соотношения а_ik = а_vk, k = 1,..., q.

2. Определение интенсивности использования рациональных спо­собов раскроя.

Обозначения:

j —индекс материала, j = 1,..., п;

k —индекс вида заготовки, k = 1,..., q;

i — индекс способа раскроя единицы материала, i = 1,..., р;

а_ijk — количество (целое число) заготовок вида k, полученных при раскрое единицы j -го материала i -м способом;

b_k — число заготовок вида k в комплекте, поставляемом заказ­чику;

d_j — количество материала j -го вида;

x_ji — количество единицу j -го материала, раскраиваемых по i -му способу (интенсивность использования способа раскроя);

c_ji — величина отхода, полученного при раскрое единицы j -го материала по i -му способу;

у — число комплектов заготовок различного вида, поставля­емых заказчику.

Модель А раскроя с минимальным расходом материалов:

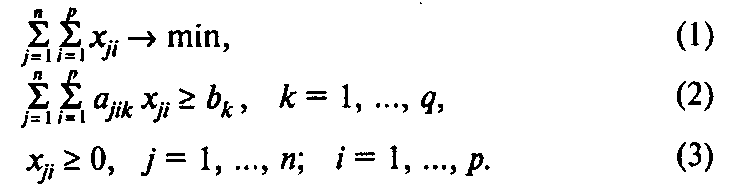
Здесь (1) — целевая функция (минимум количества использу­емых материалов);

(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(3) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являютсяограничения (2).

Модель В раскроя с минимальными отходами:

Здесь (4) — целевая функция (минимум отходов при раскрое ма­териалов);

(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(6) — условия неотрицательности переменных.

Модель С раскроя с учетом комплектации:

Здесь (7) — целевая функция (максимум комплектов, включающих заготовки различных видов);

(8) — ограничения по количеству материалов;

(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;

(10) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являютсяограничения (9).

Примеры

Пример 1. Способы раскроя металлического стержня.

Определите все рациональные способы раскроя металлического стержня длиной 100 см на заготовки трех типов: длиной 20, 30 и 50 см. Укажите величину отходов для каждого способа.

Решение. Для данного материала и указанных заготовок су­ществует семь различных рациональных способов раскроя. Все они приведены в следующей таблице:

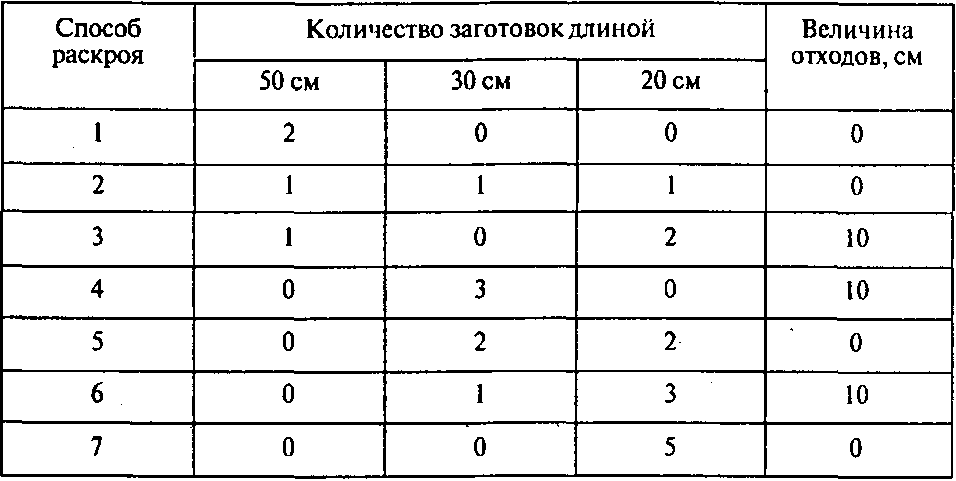Пример 2. Способы раскроя куска кожи.

Определите все рациональные способы раскроя прямоугольного куска кожи размером 100 х 60 см на квадратные заготовки со сторо­нами 50,40 и 20 см и укажите величину отходов для каждого способа.

Решение. Для данного материала и указанных заготовок су­ществует шесть различных рациональных способов раскроя:

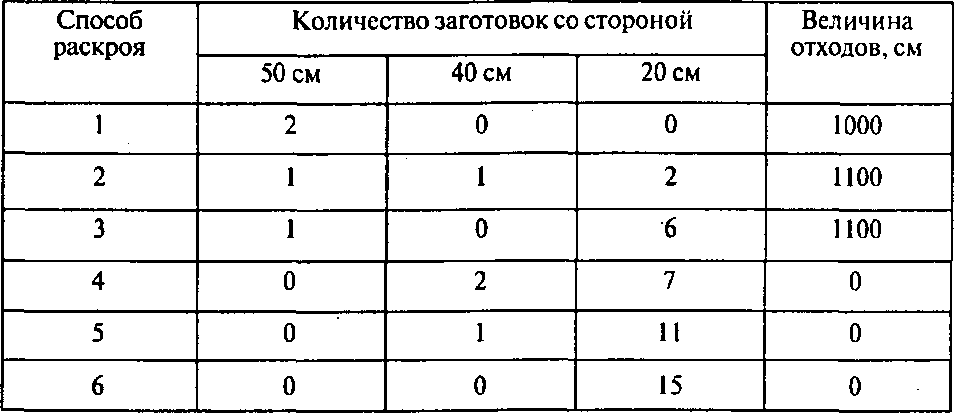
Пример 3. Изготовление парников из металлических стержней.

При изготовлении парников используется материал в виде ме­таллических стержней длиной 220 см. Этот материал разрезается на стержни длиной 120, 100 и 70 см. Для выполнения заказа тре­буется изготовить 80 стержней длиной 120 см, 120 стержней дли­ной 100 см и 102 стержня длиной 70 см.

 

7. Основная планово-производственная задача Канторовича

Модели, которые различаются видом критерия оптимальности, обладают схожими ограничениями можно обобщить, построить универсальную модель. Инструментом этого обобщения и средством придания модели свойства универсальности –это ингредиенты и технологические способы.

Игредиент – любой фактор, участвующий в производственном процессе, каковыми могут быть ресурсы разного рода, промежуточная продукция (полуфабрикаты), а также конечная продукция данного хозяйственного объекта, в чем бы она не выражалась. Итак, ингредиенты могут быть трех видов: ресурсы, промежуточная продукция, конечная продукция.

Техн. способ (технологиями, производственными способами) понимаются различные способы соединения ингредиентов в процессе производства. Это м.б виды технологических процессов (технологии в инженерном смысле), выпускаемой продукции, используемых ресурсов, по конечному (с точки зрения выбранного критерия оптимальности)эффекту. Это может быть не только технологический способ производства, но и транспортировки, хранения, оказания услуг и т.д. Итак, технологический способ жестко определен участием в нем тех или иных ингредиентов, размерами этого участия(произв-во или расход), а, следовательно, и их соотношением между собой в рамках данной технологии и, кроме того, определенным значением критериального показателя.

Производство (расходование) одного и того же ингредиента возможно в нескольких способах. В силу этого имеет место взаимозаменяемость технологических способов, а, следовательно, и возможность выбора наиболее выгодных из них. С другой стороны, в разных способах один и тот же ингредиент может то производиться, то тратиться, но может и не участвовать. Отсюда следует взаимодополнение технологических способов. Кроме того, наличие взаимозаменяемости и взаимодополняемости технологических способов ведет в конечном счете и к взаимозаменяемости ресурсов (продукции) в рамках задачи в целом, хотя в каждом из способов соотношение ингредиентов жестко закреплено, и они невзаимозаменяемы.

модель основной планово-производственной задачи Канторовича.

Введем следующие обозначения:

bj — общий объем i-го ингредиента в производственном процессе моделируемого

хозяйственного объекта; при этом, если i-й ингредиент является конечным продуктом, то bi>0, если ресурсом, то bi < 0, а если i-й ингредиент целиком производится и потребляется внутри объекта и является промежуточным продуктом, то bi =0;

a_is — норма участия i-го ингредиента в s-м технологическом способе на единицу его (т.е.способа) интенсивности; при этом, если i-й ингредиент выпускается, то a_is>0 и норма участия есть ни что иное, как величина выпуска i-го ингредиента при единичной интенсивности использования способа s, если i-й ингредиент затрачивается, то a_is< 0 и в этом случае норма участия есть норма затрат ингредиента i на единицу интенсивности способа s, если i-й ингредиент и не выпускается и не затрачивается, то a_is=0;

p_s — коэффициент эффективности s-го технологического способа в расчете на единицу его интенсивности; например, при выборе в качестве критерия оптимальности максимума прибыли величины p_s являются величиной прибыли от использования s-го технологического способа с единичной интенсивностью;

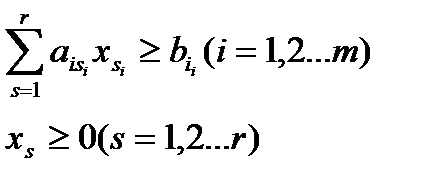x_s — интенсивность s-го технологического способа; она показывает размеры его использования при том или ином варианте плана и может измеряться через любой из ингредиентов, т.е. размером выпуска какого-либо конечного продукта (или даже промежуточного продукта), либо количеством затрачиваемого ресурса (промежуточного продукта) любого вида.

 

Более подробно обсудим, каким образом измеряется интенсивность технологических способов.

Ингредиенты	Единицы измере­ ния	Варианты значений норм участия, ais
I	II	III	IY
1.Конечная продукция А	у.е
2.Конечная продукция Б	ед.		0,5	0,2	0,25
3.Реализуемые отходы	кг
4.Сырье	т	-5	-2,5	-1	-1,25
5.Электроэнергия	кВт-ч	-7	-3,5	-1,4	-1,75
6.Оборудование	станко-ч	-2	-1	-0,4	-0,5
7.Трудовые ресурсы	чел.-ч	-10	-5	-2	-2,5
8.Емкость складов	м	-12	-6	-2,4	-3
9.Промежпрод В	шт.	-6	-3	-1,2	-1,5
10.Промежпрод Г	м			0,8
11.Прибыль на ед. инт-ти	у.е./ед.инт

Следует отметить, что в последней строке таблицы величина показателя прибыли учитывает общий итог выручки от реализации не только продукции Б, но и реализуемых отходов, а также как затраты, возникающие при расходовании ресурсов, так и затраты, связанные с выпуском и расходом промежуточной продукции В и Г соответственно. Кроме того, здесь же может учитываться и общий итог затрат и выпуска тех второстепенных видов ресурсов, конечной и промежуточной продукции, которые не были включены в модель, но в реальном процессе производства тратятся и выпускаются в рамках данной технологии.

 

 

Несмотря на различные наборы цифр в столбцах табл.2.1, все четыре варианта значений норм участия a_is соответствуют не четырем разным технологиям, а одной и той же. Однако в каж­дом из этих вариантов интенсивность одной и той же технологии измеряется по разному. В первом варианте — выпуском (в единицах) конечной продукции Б, во втором — затратами (в станко-ч) времени работы оборудования, в третьем — расходом (в т) сырья, и наконец в четвертом варианте — выпуском (в м) промежуточной продукции Г.

Нетрудно убедиться, что каждый из вариантов значений норм участия может быть получен из любого другого делением всех показателей на абсолютную величину нормы участия того ингредиента, который станет измерителем интенсивности данного технологического способа. В общем случае число таких вариантов может быть не более т, т.е. числа ингредиентов. Однако в нашем случае число возможных вариантов записи данной технологии равно не десяти, а лишь девяти, так как конечная продукция А в данной технологии не участвует. Но в общем перечне ингредиентов конечная продукция А присутствует, ибо этот перечень един для всех способов и является сквозным по всей задаче. Достаточно наличия факта выпуска или расхода ингредиента хотя бы в одном технологическом способе, чтобы этот ингредиент появился (пусть и с нулевой нормой участия) во всех остальных способах).

Выбор того или иного варианта отражения технологии в задаче зависит от степени важности ингредиентов. При одновременном изготовлении нескольких видов конечной продукции из одного сырья целесообразно за единицу интенсивности принять расход единицы этого сырья. При выпуске одной конечной продукции из многих видов сырья — выпуск единицы этой продукции. При переработке разнообразного сырья и выпуске многих видов продукции на одном оборудовании — расход единицы времени работы этого оборудования. При дефиците складов — заполнение единицы емкости склада. Кроме того, степень важности может определяться силой влияния каждого из ингредиентов на основные показатели хозяйственной деятельности предприятия (например, прибыльностью) или же иными соображениями.

В нашем примере (табл.2.1) в качестве ингредиентов выступали реальные конечные продукты, ресурсы и промежуточные продукты. Продукция А лишь для удобства измеряется в у.е. (вряд ли наше предприятие печатает деньги, производя на самом деле некие осязаемые предметы или услуги). Кроме того, в у.е. могут измеряться и ингредиенты финансовой природы: кредиты и дотации как своего рода ресурсы, платежи и отчисления как конечная продукция особого вида.

Если же технологические способы соответствуют хозяйственно самостоятельным подразделениям нашего объекта, то возможна и промежуточная продукция финансового характера.

Подобные финансовые ингредиенты олицетворяют собой отношения между людьми, коллективами, хозяйственными и административными объектами и т.п. Но кроме того, возможно появление и другой группы ингредиентов, характеризующих отношения и пропорции между процессами, происходящими внутри моделируемого объекта. Например, такой показатель как производительность труда может являться своего рода конечным продуктом нашего объекта, если мы зададим ее минимальный уровень положительной величиной bi. Тогда фактический уровень производительности труда не может быть ниже заданного и определится в левой части соответствующего ограничения как средневзвешенный из конкретных уровней производительности труда отдельных технологий. В модель, таким образом, будет включен “выпуск” показателя “производительность труда”. Наоборот, показатель “фондоемкость” будет “тратиться”, представляя собой своего рода ресурс с отрицательно заданной величиной bi, отражающей максимально допустимый уровень этого показателя.

Кроме того, в задаче возможен учет и ингредиентов внеэкономической природы, например, экономических показателей типа предельно-допустимых концентраций или выбросов, допустимого ущерба и т.п.

 

Вопрос 8.

После описания ряда конкретных моделей и их обобщения в основной планово-производственной задаче Канторовича целесообразно рассмотреть некоторые теоретические проблемы описания функционирования производственных систем.

Известно, что для описания процесса функционирования производственной системы используется метод производственных функций.

Пусть, как и выше в процессе производства система использует т видов ресурсов и пусть вектор 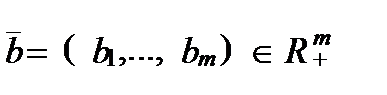характеризует данный набор используемых ресурсов. В свою очередь, производственная система включает определенный набор технологических способов производства: Т ₁,..., Т_r, при этом по s -му способу выпускается продукция s -го наименования, в производстве которой используются все виды ресурсов или только некоторая их часть. Производственная функция связывает объем потребляемых по s -й технологии ресурсов с величиной выпуска валовой (в натуральных единицах) или товарной (в стоимостном выражении) продукции s -го наименования.

Таким образом, 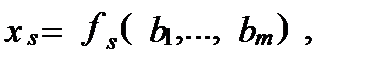где х_s — объем продукции, выпускаемой по s -й технологии, f_s — соответствующая производственная функция (ПФ).

Если математическая сущность ПФ заключается в том, что она задает отображение множества наборов ресурсов 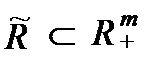на множество товарных выпусков 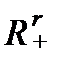, то экономическая сущность ПФ заключается в том, что соотношение выражает объем продукции, выпущенной по s -й технологии, при наиболее рациональном использовании ресурсов. Основной целью функционирования системы управления производством является выбор вектора ресурсов , а также способа реализации технологии Т_s, при котором будет реализован “оптимальный” способ использования ресурсов.

Производственная функция является одним из основных инструментов планово-производственных расчетов при анализе производственно-коммерческой деятельности промышленной фирмы. Как будет ясно из дальнейшего, ПФ объектов микроэкономики могут быть как линейными, так и (очень часто) нелинейными.

Рассмотрим очень важный для модельных приложений случай, когда технологическое множество производственной системы является линейным выпуклым множеством. В этом случае модель производства оказывается линейной.

Основная предпосылка возможного применения этой модели состоит в том, что любой происходящий производственный процесс можно представить в виде линейной комбинации с неотрицательными коэффициентами некоторых основных (или базовых) производственных процессов. В свою очередь, каждый из этих процессов задается при помощи вектора “выпуск-затраты”, размерность которого определяется суммой количества видов производимых продуктов и потребляемых ресурсов. Коэффициенты в разложении данного производственного процесса по базовым производственным процессам назовем, как и выше, интенсивностями основных способов.

Одним из примеров, характеризующих сказанное, является интерпретация основного производственного способа как производства продукции и расхода ресурсов в единицу времени. В этом случае величины интенсивностей выражают собой, например, количество смен работы некоторого производственного участка по какой-либо из r технологий. В этом случае основные показатели выпуска продукции и затрат ресурсов на всем производстве являются суммой выпусков и затрат отдельных участков. Последнее и служит основой для представления модели производства как линейной.

Дадим теперь строгие предположения относительно множества технологий Т ₁,..., Т_r, которые приводят к линейным моделям.

Предположение 2.1 (об однородности технологических способов или закон постоянства удельного выпуска независимо от масштаба производства):

если то для всякого a >0справедливо

Это предположение означает, что если технологически допустимым является вектор 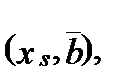то технологически допустимы также векторы “выпуск-затраты”, у которых выпуск увеличивается (уменьшается) в a раз при одновременном увеличении (уменьшении) затрат также в a раз.

Предположение 2.2 (об аддитивности технологических способов):

если а 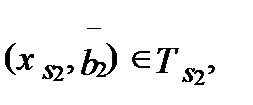то существует такая технология Т, для которой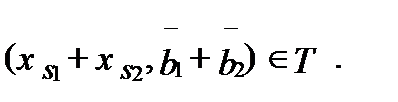

Это предположение означает, что, если возможен выпуск продукции s ₁-го наименования в количестве 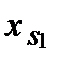при затратах вектора ресурсов , а также выпуск продукции s ₂-го наименования в количестве 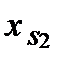при затратах вектора ресурсов , то допустимым является выпуск вектора 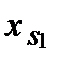+ 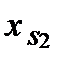при затратах ресурсов + .

Предположение 2.3 (о линейной структуре множества технологий):

существует конечное число основных технологических способов (каждый из которых является вектором “выпуск-затраты”): Р ₁,..., Р_К таких, что для любого технологически допустимого набора найдутся такие неотрицательные числа b ₁,..., b_К, что справедливо соотношение

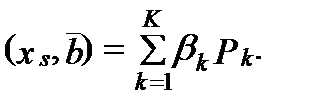
Замечание. Совместно предположения 2.1 и 2.2 означают, что технологическое множество является выпуклым конусом. Предположение 2.3, выделяющее линейные технологии, означает, что этот конус является выпуклым многогранником в полупространстве .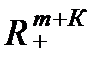

Таким образом, в качестве основного параметра линейной производственной системы можно принять вектор основных производственных способов Р ₁,..., Р_К . При этом характеристикой внутреннего состояния системы следует считать неотрицательный вектор их интенсивностей 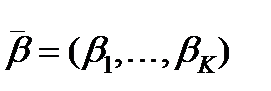. Вектор 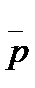, описывающий функционирование всего производства, имеет вид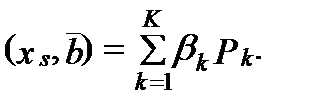

При помощи ограничений на компоненты вектора 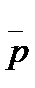формируются производственные и ресурсные ограничения на множества допустимых значений интенсивностей основных технологических процессов. Кроме того, каждая производственная система обладает специфическими ограничениями на интенсивности отдельных технологических способов, обусловленными особенностями производства.

На множестве возможных состояний формируется некоторое правило выбора наилучшего или оптимального состояния производственной системы. Наиболее часто это правило имеет содержательный смысл выпуска наибольшего количества продукции, максимального увеличения прибыли или минимизации затрат. Иногда это правило формулируется путем постановки задачи многоцелевой оптимизации.

 

 

Вопрос 9.

В качестве примера рассмотрим простейшую модель оптимизации производства по критерию максимума дохода в случае, когда для производства j -й продукции используется один технологический способ производства Т_j (j = 1,2,..., n). Пусть р_j — доход от реализации продукции, изготовляемой однократным применением j -й технологии. Тогда вектор “выпуск-затраты”, описывающий j -й производственный способ имеет вид Р_j =(р_j; a_1j, a_2j,..., a_ij,..., a_nj), где a_ij — затраты i -го ресурса (i =1,2,..., т) при однократном применении j -й технологии. Будем считать, что затраты исчисляются в стоимостном выражении. Таким образом, каждая компонента вектора Р_j суть стоимость или затрачиваемых производственных факторов, или произведенной продукции.

Состояние производственной системы задается вектором 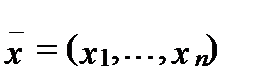интенсивностей использования технологий Т ₁,..., Т_n.

Вектор “выпуск-затраты”, описывающий функционирование производственной системы, имеет вид 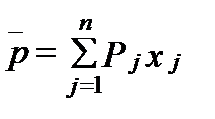. При этом выпуск товарной продукции равен , а затраты i -го ресурса составляют величину .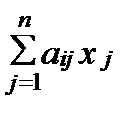

 

Если целью функционирования производственной системы является максимизация выпуска товарной продукции, то модель производственной системы представляется в следующем виде:

® max; (2.7)

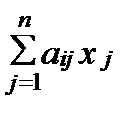£ b_i (i= 1,2,..., m); (2.8)

х_j ³ 0 (j= 1,2,..., n). (2.9)

Задача нахождения оптимального состояния производственной системы в данном случае является задачей линейного программирования.

Пусть — одно из решений задачи линейного программирования. В этом случае наибольшая величина выпуска определяется числом .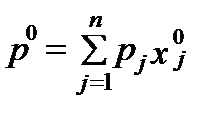

Для нахождения оптимального решения 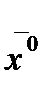в задаче (2.7)-(2.9) приведем систему ограничений модели к каноническому виду. Для этого ограничения (2.8), (2.9) превратим в уравнения, введя переменные t_i ³0, экономический смысл которых — количество неиспользованных ресурсов вида i:

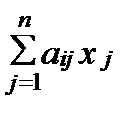+ t_i = b_i (i= 1,2,..., m). (2.10)

Задача линейного программирования (2.7), (2.10), (2.9) с дополнительными ограничениями на неотрицательность переменных t_i имеет размерность n + m. При этом число базисных переменных в случае линейной независимости системы ограничений (2.8) равно числу ограничений, т.е. m, а число свободных переменных совпадает с числом неизвестных в линейной форме (2.7), т.е. равно n. Обозначим через с значение целевой функции в форме (2.7).

В исходном опорном плане задачи будем считать переменные группы t_i базисными переменными, а группы x_j — свободными. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу линейного программирования (2.7),(2.10), (2.9) в следующем виде:

с = 0 - 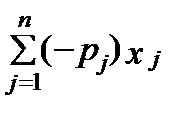® max; (2.11)

t_i = b_i - 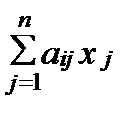, t_i ³0(i= 1,2,..., m); (2.12)

х_j ³ 0 (j= 1,2,..., n). (2.9)

Задача (2.11), (2.12), (2.9) может быть представлена следующей матрицей коэффициентов при переменных:

. (2.13)

 

В матрице (2.13) коэффициенты первой строки совпадают с коэффициентами линейной формы (2.11): a ₀₀ = 0, a ₀₁ = - p ₁,..., a_0n = - p_n, а коэффициенты первого столбца — с коэффициентами правых частей ограничений (2.8): a ₁₀ = b ₁,..., a_i0 = b_i ,..., a_m0 = b_m.

По виду коэффициентов матрицы (2.13) легко судить, является ли найденное базисное решение допустимым и, если оно допустимо, то будет ли оптимальным. Действительно, замечая, что столбец коэффициентов a_i0 , i ¹0представляет собой базисное решение, соответствующее базису t ₁,..., t_m, а строка коэффициентов a_0j , j ¹0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении для с, приходим к выводу, что базисное решение, соответствующее базису t ₁,..., t_m, допустимо если a_i0 ³0 (в нашем случае это действительно так: a_i0 = b_i >0). Если, кроме того, a_0j ³0, то это базисное решение является и оптимальным, так как линейная форма (2.11) принимает наибольшее значение, равное a ₀₀ , при равенстве нулю свободных переменных (в нашем случае это условие не выполняется, так как все элементы первой строки матрицы (2.13) неположительны). Таким образом, матрица (2.13) соответствует допустимому базисному решению, но не оптимальному.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: