 |
Маятники пружинный, математический, физический.
|
|
|
|
Гармонический осциллятор, его закон движения, скорость, ускорение, возвращающая сила, энергия.
Гармонический осциллятор – система, совершающая колебания, описываемые дифференциальным уравнением гармонических колебаний: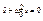 
. Решением этого уравнения является выражение: 
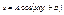(*), где A – максимальное значение колеблющейся величины (амплитуда колебания), ω0 – круговая (циклическая) частота, φ – начальная фаза колебания в момент времени t =0, (ω0t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до –А.
За период колебаний фаза колебания получает приращение 2 π, т.е.: 
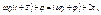откуда: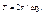 
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (*), где s = x: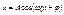 
Скорость и ускорение – это первая и вторая соответственно производные от х:
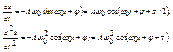
Сила F = ma, квазиупругая или упругая сила. Под квазиупругой (как бы упругой) понимают неупругую по природе силу, величина которой пропорциональна точки от положения равновесия, а направление – противоположно смещению, т.е. для квазиупругих сил это равенство также справедливо.
действующая на колеблющуюся м.т. массой m вышенаписанных уравнений, равна:
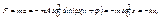где 
.
Пружин. Маятник действует под квазиупругой силой, а мат. И физич. – под упругими силами.
Кинетическая энерги я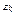 
м.т., совершающей прямолинейные гармонические колебания равна: 
или 
Потенциальная энергия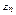 
м.т., совершающей гармонические колебания под действием упругой силы F, равна 
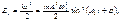или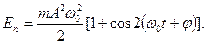 
|
|
|
Полная энергия Е: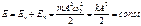 
. 
ВЫВОДЫ: 1. Колебания возникают при условии: а) положения равновесия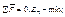 
б) возвращающая сила 
в) инертность, m. 2. 
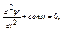где ψ - колеблющаяся величина (x, v, A, F).
Если уравнение движения имеет такой вид, то это гармонические колебания с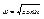 
.
3. Частота собственных колебаний определяется параметрами колебательной системы и не зависит от внешних условий, в частности, от запаса энергии, сообщенной осциллятору при возбуждении колебаний.
4.При гармонических колебаниях механического осциллятора гармонически колеблются с одинаковыми частотами и согласованными амплитудами и фазами смещение, скорость, ускорение, возвращающая сила при сохранении полной энергии, тогда как кинетическая и потенциальная энергии колеблются с удвоенной частотой.
Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
Маятники пружинный, математический, физический.
1. Пружинный маятник – это груз массой m, подвешенный на абсолютно-упругой пружине и совершающий гармонические колебания под действием упругой силы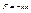 
, где k – жесткость пружины. Уравнение движения маятника:
или 
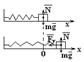Пружинный маятник совершает гармонические колебания по закону: 
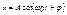с циклической частотой 
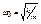и периодом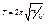 
Потенциальная энергия пружинного маятника: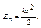 
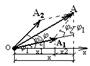
2. Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С.
Если маятник отклонен от положения равновесия на некоторыйугол α, то в соответствии с уравнением динамики вращательного движения твердого тела: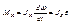 
момент М возвращающей силы можно записать в виде: 
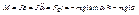, где J – момент инерции маятника относительно оси, проходящей через точку подвеса О, l – расстояние между ней и центром масс маятника, Fτ - возвращающая сила.
|
|
|
Запишем предыдущее уравнение в виде: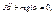 
или 
Принимая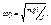 
получим уравнение 
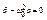(гармонический осциллятор), решение которого: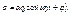 
Период физического маятника: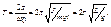 
, где 
-приведенная длина физического маятника.
3. Математический маятник – это идеализированная система, состоящая из м.т. массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести.
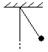Момент инерции математического маятника: 
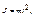где l –длина маятника.
Т.к. математический маятник можно представить, как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке – центре масс, то, подставив формулу момента инерции в формулу периода физического маятника, получим выражение для периода малых колебаний математического маятника: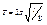 
Роль возвращающей силы при колебаниях физического и математического маятников играет составляющая силы тяжести, которая является консервативной, поэтому полная механическая энергия колебаний сохраняется.
|
|
|
