Классификация точек разрыва

Модуль 2

Лекция 13. Непрерывность функций

13.1.Непрерывность в точке и на промежутке.

13.2.Классификация точек разрыва

13.3.Непрерывность основных элементарных функций

Программные положения

«Приступая к изучению функциональных зависимостей, мы должны, конечно, прежде всего с помощью целесообразной классификации внести хотя бы некоторый порядок в предстоящий нам многообразный мир. Первым таким классифицирующим и организующим принципом служит обычно (и с полным основанием) разделение всех функций на непрерывные и разрывные, причем математический анализ имеет дело почти исключительно с непрерывными функциями, ишь в сравнительно редких случаях привлекая к рассмотрению и простейшие из разрывных. Непрерывные функции обладают целым рядом особых свойств, которых лишены, вообще говоря, функции разрывные; благодаря этим свойствам исследование и применение непрерывных функций весьма значительно облегчаются, так что изучение этих свойств становится для анализа чрезвычайно важным делом» (А.Я.Хинчин «8 лекций по математическому анализу»)

Методические рекомендации

Внимательно прочитайте текст лекции, разберите примеры. Уделите внимание анализу непрерывности основных элементарных функций и связи непрерывности в точке и предела функции в этой точке.

Литература

А.В.Дорофева «Высшая математика» глава 7 «Непрерывность и разрывы функций» стр.160-178

Б.П.Демидович, В.А.Кудрявцев Краткий курс высшей математики» Глава VIII Непрерывность функции» стр.133-144

Дополнительно

Р.Курант, Г.Роббинс «Что такое математика?» Глава VI «Функции и пределы» §4,5,6 стр. 337-349; Дополнение к главе VI § 1-2 стр. 349-357

 

 

Контрольные вопросы

1. Дайте определение функции, непрерывной в точке, на промежутке

2. Какова связь между определением предела функции и непрерывности в точке?

3. Что такое точки разрыва первого и второго рода?

4. Приведите примеры непрерывных и разрывных функций

5. Что необходимо проверить, чтобы убедиться, что в данной точке функция непрерывна?

6. Доказать, что функция y=x³ является непрерывной в произвольной действительной точке х₀

7. Проанализируйте непрерывность основных элементарных функций

Непрерывность в точке и на промежутке.

Определение 13.1(1)

Пусть f(x) — вещественнозначная функция, определенная в некоторой окрестности точки

x₀ .

Описательно говоря, функция f(x) непрерывна в точке x₀, если ее значения f(x) по мере приближения аргумента х к точке x₀ приближаются к значению f(x₀) функции в самой точке x₀.

Уточним теперь это описание понятия непрерывности функции в точке.

Дадим формальное определение:

Функция f(x) называется непрерывной в точке x₀, если для любой окрестности V(f(x₀)) значения f(x₀) функции в точке x₀ найдется такая окрестность U(x₀) точки x₀, образ которой при отображении f содержится в V(f(x₀)).

 

Иначе говоря,

Функция y = f (x) называется непрерывной в точке x = x ₀, если она определена в этой точке и ее значение f (x ₀) равно пределу функции в этой точке: .

Отсюда следует, что ,

что, используя обозначения

можно записать как

 

На языке ε и δ:

 

Каково бы ни было число ε>0, для него найдется такое число δ>0, что неравенство

 

 

Примеры 13.1(1)

 

1. Рассмотрим функцию f(x) = 1/x (см. рис. 13.1(1)) и покажем, что она непрерывна во всех точках, кроме х₀ = 0.

Рис.13.1(1)

 

 

2. Покажем, что функция y = x ² непрерывна в произвольной точке x₀

Согласно свойствам предела суммы и произведения

 

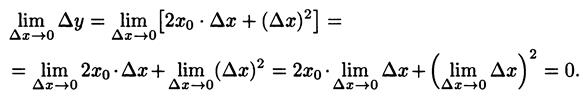
Таким образом,

, что и означает, по определению, непрерывность в точке x₀.

 

 

3. Покажем, что функция f(x)=sin x непрерывна на

 

Для любой точки выполняется

 

Определения 13.1(2)

Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.

 

Функция f (x) называется непрерывной в точке a справа (непрерывной в точке b слева), если

().

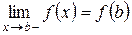Функция непрерывна справа в точке x =0.

Функция называется непрерывной на замкнутом промежутке [ a, b ], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

 

Если функция f: X не является непрерывной в некоторой точке множества X, то эта точка называется точкой разрыва функции f.

 

Таким образом, для того, чтобы функция f(x) была непрерывна в некоторой точке а необходимо:

1) Чтобы функция была определена в окрестности точки а

2)чтобы в этой точке существовали (конечные)односторонние пределы

3)они должны совпадать между собой

4)они должны совпадать со значением функции в этой точке

 

Примеры 13.1.

1.Рассмотрим функцию «знак» y = sign x, определенную следующим образом:

 

, ее график см. на рис. 13.1(2)

Рис. 13.1(2)

 

В точке 0 односторонние пределы существуют, но они различны (-1 слева и +1 справа), кроме того, ни один из них не совпадает со значением функции в точке х=0, равного 0.

 

2. У функции y = |sign x| (график см. на рис. 13.1(3)) односторонние пределы существуют, совпадают, равняясь 1, но не совпадают со значением 0 функции в точке х=0

 

Рис. 13.1(3)

 

 

3.

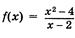
Эта функция не определена при х=2, несмотря на то, что существуют и совпадают конечные односторонние пределы в этой точке.

 

Рис.13.1(4)

 

4. Функция Дирихле χ(х)

χ (х) = 1, если х рационально

χ (х) = 0, если х - иррационально

 

Так как в любой близости от рациональной точки найдутся точки иррациональные, и наоборот, то каково бы ни было х₀ в промежутке (-∞, +∞), предела χ (х) при не существует, так что в каждой точке имеет место разрыв второго рода (с обеих сторон)

 

 

Приведем без доказательства основные свойства непрерывных функций, непрерывных в точке

 

Теорема 13.1.1

Если функции f(x), g(x) непрерывны в точке х₀, то в этой точке непрерывны и функции af(x),

, a – действительное число

 

Теорема 13.1.2. Непрерывность сложной функции (композиции)

Пусть функция u(х) непрерывна в точке х_о, а функция f(u) непрерывна в точке u_о =

= u(x₀). Тогда сложная функция f(u(x)) непрерывна в точке х_о.

 

 

Приведем без доказательства основные свойства непрерывных на промежутке функций

 

Теорема 13.1.3 Больцано-Коши

Пусть функция f(x) определена и непрерывна на отрезке [а; b] и принимает на его концах разные знаки.

Тогда найдется хотя бы одна такая точка , что f(x₀) = 0

 

Теорема 13.1.4 О промежуточных значениях

 

Пусть функция f(x) определена и непрерывна на отрезке [а;b]. Тогда для любого числа

С, заключенного между числами f(a) и f(b), найдется такая точка

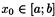, что f(x₀) = С.

 

 

Теорема 13.1.5 (1-я теорема Вейерштрасса)

Пусть функция f(x) определена и непрерывна на отрезке [а;b]. Тогда эта функция ограничена

на этом отрезке.

 

Теорема 13.1.6 (2-я теорема Вейерштрасса)

Пусть функция f(х) определена и непрерывна на отрезке [а; b]. Тогда эта функция принимает

на отрезке [а;b] свои наибольшие и наименьшие значения, т.е. существуют такие точки 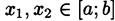, что для любой точки справедливы неравенства

f(x₁) ≤ f(x) ≤f(x₂).

 

 

Классификация точек разрыва

 

Определения13.2(1)

Точка х₀ разрыва функции f(x) называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции и хотя бы один из них не совпадает со значением функции в данной точке

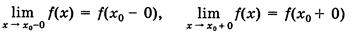(см. рис.13.2, точка а – точка разрыва первого рода)

 

 

При этом функция f(x) не обязательно должна быть определена в точке х₀, то есть f(х₀) может и не существовать

 

Величина называется скачком функции в точке х₀.

 

 

Все остальные точки называются точками разрыва второго рода (в этих точках односторонние пределы либо не существуют, либо бесконечны) (см. рис. 13.2(2) – точка О – слева разрыв 2 рода – предел не существует; точка 3 – слева разрыв 2 рода (бесконечный предел)

Рис. 13.2(2)

 

Поделиться:

Воспользуйтесь поиском по сайту: