Основные правила комбинаторики

1. Правило суммы.
Число способов, с помошью которых можно выбирать элементы непересекающихся n- и m-множеств, равно .

2. Правило произведения.
Число способов выбора элементов множества С равно декартову произведению множеств A и B, т.е. .

Пересчёт упорядоченных выборок (перестановок)

Перестановки с повторением

Число упорядоченных выборок с повторением равно .

Пусть

Перестановки без повторения

Число упорядоченных выборок без повторения равно .

Пусть

Пересчёт неупорядоченных выборок (сочетаний)

Сочетания с повторением

Число сочетаний с повторением равно .

Сочетания без повторения

Число сочетаний без повторения равно .

Метод включений и исключений

Число элементов n-множества А, не обладающим ни одним из N свойств, равно

Метод рекуррентных соотношений. Треугольник Паскаля

Рекуррентным называется соотношение, в котором для вычисления некоторого члена числовой последовательности используются значения предыдущих членов последовательности.

Суть метода состоит в том, что комбинаторная задача может быть решена с меньшим количеством переменных.

.

На основании полученного соотношения составляетя треугольник Паскаля:

r

n

Вычисления производятс по формуле .

Последовательность Фибоначчи:

Ряд чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21,…

Решение линейных рекуррентных соотношений

 

Для выполнения вычисления любого члена числовой последоввательности необходимо вычислить все пердыдущие. Для быстрого вычисления числовой последовательности удобнее иметь формулу для её вычисления в явном виде как ыункцию номера вычисляемого элемента в рассматриваемой числовой последовательностию Эта задача решается для рекуррентного соотношения формулы последовательности Фибоначчи следующим образом:

1. Пусть , тогда (1)

2. Пусть тогда разделим равенство (1) на Получим
Полученное уравнение имеет два корня

3. Общее решение рекуррентного соотношения находим по формуле (2)
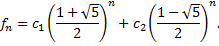Пусть , .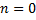

4. Получаем, что (3) Эта формула носит название формулы Бине.

В общем случае линейное рекуррентное соотношение имеет вид (4)

Решение формулы (4) ищем в виде 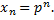Подставляя в формулу (4) получаем, что (5)
Это уравнение имеет корней. Общее решение принимает вид (6)
Неизвестные коэффициенты находятся при помощи использования начальных условий, которые позволяют составить систему линейных уравнений относительно этих коэффициентов.

Граф. Основные понятия

Графом называется двойка – множество вершин графа, а – множество рёбер (дуг) графа.

Ребро графа задаётся неупорядоченной парой , а дуга (ориентированное ребро) – упорядоченной парой .

Неориентированный граф состоит только из неориентированных рёбер. Ориентированный – только из ориентированных. Смешанный – из ориентированных и неориентированных.

Ребро называется петлёй, если оно начинается и заканчивается в одной и той же вершине.

Вершина инцидентна ребру, если она – одна из концевых вершин этого ребра. Вершины называются смежными, если они инцидентны одному ребру.

Вершина называется изолированной, если она не инцидентна ни одному ребру.

Если в графе хотя бы одну пару вершин соединяет больше одного ребра, такой граф называется мультиграфом.

Граф называется полным, если каждая пара его вершин соединена ребром.

Граф называется двудольным, если множество его вершин можно разбить на два непересекающихся множества так, что каждое ребро графа иемеет концевые вершины, принадлежащие разным множествам.

Способы задания графа

1. Матрица смежности

2. Матрица инцидентности

3. Список рёбер

4. Структура смежности

 

Предшественник	Последователь
	-
	1, 4

Операции над графами

1. Объединение

2. Пересечение

3. Дополнение

4. Композиция

5. Удаление вершины

6. Стягивание ребра

7. Удаление ребра

Связность графов

Если имеем граф , то марштутом графа M называется последовательность вершин и рёбер.

Число рёбер маршрута называется его длиной.

Маршрут также задают последовательностью составляющих его рёбер или вершин.

Граф называется связным, если между любыми его двумя рёбрами существует маршрут М. Связной граф образует компоненту связности. Граф может иметь несколько компонент связности. Граф на рис. 2а имеет две компоненты связности: одна порождается вершинами v₁, v₂, v₃ и v₅, а другая – v₄.

Компоненту связности определяют как некоторую часть графа G, которую можно нарисовать, не отрывая пера от бумаги, даже проходя по одному и тому же ребру несколько раз.

Маршрут назывется цепью, если в нём нет повторяющихся рёбер. Цепь называется простой, если в ней нет повторяющихся вершин. В орграфе цепь назывется путём.

Если в некотором пути начальная и конечная вершины совпадают, такая цепь называется циклом. В орграфе цепь называется контуром.

Числа графов

1. Локальная степень вершины

2. Цикломатическое число графа.
,
где – число рёбер, – число вершин, – число компонент связности.
Цикломатическое число графа определяет, сколько рёбер необходимо удалить из графа, чтобы он не имел циклов.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: