 |
Свойства определенного интеграла
|
|
|
|
Свойства определенного интеграла
1. Определенный интеграл не зависит от обозначения переменной, то есть
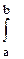f(x)dx= 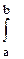f(t) dt= 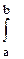f(u)du=...
так как интегральные суммы представляют собой числа, не зависящие от того, какой буквой обозначен аргумент подыинтегральной функции.
2. Определенный интеграл от суммы конечного числа непрерывных функций f1(x), f2(x), ... fn(x), заданных на отрезке [a, b], равен сумме определенных интегралов от слагаемых функций:
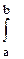[f1(x)+f2(x)+... +fn(x)]dx= 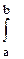f1(x)dx+ 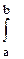f2(x)dx+... + 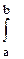fn(x)dx.
3. Постоянный множитель k подынтегральной функции можно выносить за знак определенного интеграла:
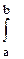k f(x)dx=k 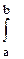f(x)dx.
4. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолютную величину и изменит свой знак на противоположный:
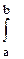f(x)dx=-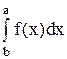 
Если пределы интегрирования равны между собой (a=b), то определенный интеграл равен нулю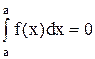 
5. 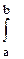dx=b-a при a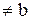 
6. Если отрезок интегрирования [a, b] разбит на две части [a, c] и [c, b], то
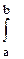f(x)dx=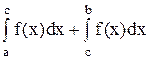 
7. Если подынтегральная функция в отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, то есть если f(x)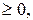 
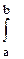то и f(x)dx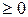 
8. Оценка определенного интеграла сверху и снизу. Значение определенного интеграла заключено между произведениями наибольшего и наименьшего значений подынтегральной функции на длину интервала интегрирования, то есть
m(b-a)< 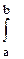f(x)dx< M(b-a), a< b, где m и M -соответственно наименьшее и наибольшее значения функции f(x) в отрезке [a, b]; m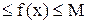 
9. Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=с отрезка интегрирования [a, b] на длину отрезка (b-a):
|
|
|
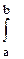f(x)dx=f(c). (B-a) или f(c) = 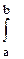f(x) dx / (b-a) или
f(c)=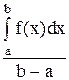 
СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1. Вычисление определенных интегралов по формуле Ньютона-Лейбница.
Согласно формуле Ньютона- Лейбница, определенный интеграл вычисляется при помощи неопределенного интеграла.
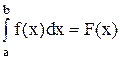
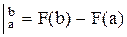
F(x)-первообразная функции f(x).
Пример: Вычислить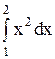 
.
Решение: =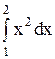 
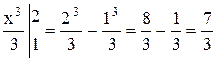
Пример: Вычислить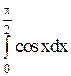 
.
Решение: 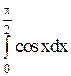=sin x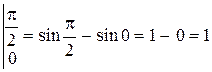 
2. Замена переменных в определенных интегралах.
Определенный интеграл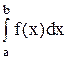 
может быть вычислен с помощью введения новой переменной, если выполнены следующие условия:
1) функция f(x) непрерывна на отрезке [a, b],
2) отрезок [a, b] является множеством значений функций x=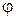 
(t), определенной на отрезке 
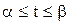и имеющей на нем непрерывную производную;
3) 
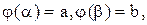
тогда справедлива формула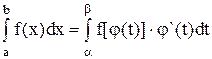 
Пример: Вычислить интеграл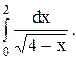 
Решение: Введем новую переменную t=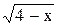 
, из которой x=4-t2,
dx=-2tdt.
Определим 
новые пределы интегрирования: из равенства t= 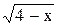при х1=0 получаем t1=2, при х2=2, t2=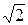 
Дифференциальным уравнением называется уравнение, связывающее независимую функцию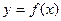 
и ее производные 
, 
.
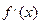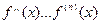Дифференциальное уравнение в общем виде записывается так: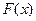 
, 
, 
.
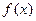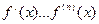Определение.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, 
- уравнение 1- порядка, а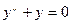 
- уравнение 2-порядка.
Определение.
Решением или интегралом дифференциального уравнения называется всякая функция 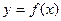, которая будучи подставлена в уравнение, превращает его в тождество.
Получаемое в результате интегрирования дифференциального уравнения решение содержит в общем случае произвольные постоянные, число которых равно порядку заданного дифференциального уравнения. Такое решение называется общим решением или общим интегралом дифференциального уравнения и записывается в виде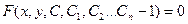 
или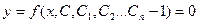 
.
|
|
|
Решения, полученные из общего решения дифференциального уравнения путем задания произвольным постоянным определенных численных значений, называются частными. На практике численные значения определяются, исходя из условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий и записывается так:
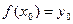или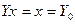 
|
|
|
