Правила введения и удаления кванторов

П1. Если дана формула (F₁(t)®F₂(x)) и F₁(t) не содержит свободной переменной x, то формула (F₁(t)®"x(F₂(x))) выводима в исчислении предикатов, т.е.

(F₁(t)® F₂(x))

(F₁(t)® "_x(F₂(x))).

П2. Удаление квантора всеобщности

 

"_x(F(x))

F (t).

П3. Введение квантора существования

 

F(t)

$_x(F(x)).

П4. Удаление квантора существования

$_x(F(x))

F(a).

П 5. Смена квантора:

"_x(F(x)) $_x(F(x))

ù$_x(ùF(x)), ù"_x(ùF(x)).

П6. Перенос квантора, если t не содержит переменной x:

 

Â_x(F₁(x))Ú F₂(t) Â_x(F₁(x))&F₂(t)

Â_x(F₁(x)Ú F₂(t)), Â_x(F₁(x)& F₂(t)), где Â_xÎ{"_x,$_x},

F₁(t)® Â_x(F₂(x)) "_x(P(x))®F(t) $_x(P(x))®F(t)

Â_x(F₁(t)®F₂(x)), $_x(P(x)®F(t)), "_x(P(x)®F(t)).

П7. Введение новой переменной:

"_x(F₁(x))Ú"_x(F₂(x)) $_x(F₁(x))&$_x(F₂(x))

"_y"_x(F₁(y)Ú F₂(x)), $_y$_x(F₁(y)Ú F₂(x)).

Все правила введения и удаления логических связок, принятые в логике высказываний, применимы также и в логике предикатов, если в них вместо формул алгебры высказываний подставить формулы алгебры предикатов.

Правила заключения

а) если F₁ и (F₁®F₂) выводимые фор­мулы в исчислении предикатов, то F2 также выводима.

Это - правило modus ponens (m.p): F₁; (F₁®F₂)

F₂.

 

b) если ùF₂ и (F₁®F₂) выводимые формулы в исчислении предикатов, то ùF₁ также выводима. Это - правило modus tollens (m.t):

ùF₂; (F₁®F₂)

ùF1.

Эти правила формируют схему вывода и позволяют, используя правила подстановки, введения и удаления кванторов, делать вывод об истинности заключения.

Метод дедуктивного вывода

В логике предикатов вывод заключения формируется так же, как в исчислении высказываний. Все правила вывода логики высказываний включены в множество правил логики предикатов.

Пример: “Таможенные чиновники обыскивают каждого, кто въезжает в страну, кроме высокопоставленных лиц. Если некоторые люди способствуют провозу наркотиков, то на внутреннем рынке есть наркотик. Никто из высокопоставленных лиц не способствует провозу наркотиков. Следовательно, некоторые из таможенников способствуют провозу наркотиков?”

Пусть P₁(x):=”x - таможенный чиновник”, P₂(x,y):=”x обыскивает y”, P₃(y):=”y въезжает в страну”, P₄(y):=”y – высокопоставленное лицо”, P₅(y):=”y способствует провозу наркотиков”.

"_y(P₃(y)&ùP₄(y)®"_x(P₁(x)&P₂(x,y)));

$_y(P₃(y)&P₅(y));

"_y(P₃(y)&P₄(y)®ùP₅(y));

$_x(P₁(x)&P₅(x)).

· F₁=$_y(P₃(y)&P₅(y)) - посылка;

· F₂=P₃(a)&P₅(a) - заключение по F₁ и правилу П4 ИП;

· F₃= P₃(a) - заключение по F₂ и правилу П2 ИВ;

· F₄= P₅(a) - заключение по F₂ и правилу П2 ИВ;

· F₅="_y(P₃(y)&P₄(y)®ùP₅(y)) - посылка;

· F₆=P₃(t)&P₄(t)®ùP₅(t) - заключение по F₅ и правилу П2 ИП;

· F₇=ùP₃(t)ÚùP₄(t)ÚùP₅(t) - заключение по F₆ и ее эквивалентным преобразованиям;

· F₈=ùP₄(a) - заключение по F₇ при t=a;

· F₉="_y(P₃(y)&ùP₄(y)®"_x(P₁(x)&P₂(x,y))) - посылка;

· F₁₀="_y"_x(P₃(y)&ùP₄(y)®(P₁(x)&P₂(x,y))) - заключение по F₉ и правилу П6 ИП;

· F₁₁=P₃(a)&ùP₄(a)®P₁(t)&P₂(t,a) - заключение по F₁₀ и правилу П2 ИП;

· F₁₂= P₃(a)&ùP₄(a) - заключение по F₃ и F₈ и правилу введения логической связки конъюнкции П1. ИВ;

· F₁₃=(P₁(t)&P₂(t,a)) - заключение по F₁₁ и F₁₂ и правилу modus ponens;

· F₁₄= P₁(t) - заключение по F₁₃ и правилу удаления логической связки конъюнкции П2. ИВ;

· F₁₅=P₅(a)=P₅(t) - заключение по F₄ и замене предметной постоянной термом;

· F₁₆= P₁(t)&P₅(t) - заключение по F₁₄ и F₁₅ и правилу введения логической связки конъюнкция П1. ИВ;

· F₁₇=$_x(P₁(x)&P₅(x)) - заключение по F₁₆ и правилу введения квантора существования П3. ИП.

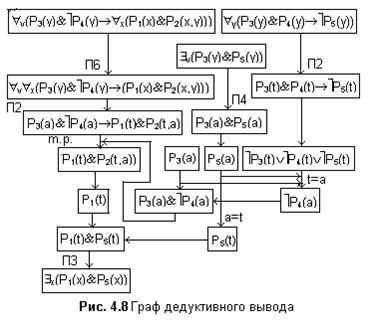
Для демонстрации процесса вывода на рис. 4.8 приведен граф.

Так доказана истинность формулы $_x(P₁(x)&P₅(x)) при заданном наборе посылок и правил вывода.

Пример: доказать истинность заключения

"_x($_y(P₁.(x, y)&P₂(y))®$_y((P₃(y)& P₄.(x, y))); ù$_x(P₃(x))

ù$_x(P₃(x))®"_x"_y(P₁.(x, y)®(ùP₂(y))).

· F₁="_x($ _y(P₁.(x, y)&P₂(y))®$_y((P₃(y)& P₄.(x, y))) - посылка;

· F₂=ù $_x(P₃(x)) - посылка;

· F₄=ùP₃(t) - заключение по F₃ и правилу П2;

· F₅=ùP₃(t)ÚùP₄.(x, t) - заключение по F₄;

· F₆="_y(ùP₃(y)Ú(ùP₄ (x, y))) - заключение по F₅ и правилу П1;

· F₇=ù$_y(P₃(y)&P₄(x; y)) - заключение по F₆ и правилу П5;

· F₃="_x(ùP₃(x)) - заключение no F₂ и правилу П5;

· F₈=$_y(P₁.(t, y)&P₂(y))$_y(P₃(y)&P₄.(t, y)) - заключение по F₁ и правилу П2;

· F₉=ù$y(P₁.(t, y)&P₂(y)) - заключение пo F₇ и F₈при t=x и правилу m. t.;

· F₁₀="_y(ùP₁.(t, y)ÚùP₂(y)) - заключение по F₉ и правилу П5;

· F₁₁="_y(P₁.(t; y)®ù(P₂(y))) - заключение по F₁₀;

· F₁₂="_x"_y(P₁.(x; y)®ù(P₂(y)) - заключение по F₁₁ и правилу П1;

· F₁₃=ù$_x(P₃(x))®"_x"_y(P₁.(x, y)®(ùP₂(y))) – заключение по F₂ и F₁₂ и правилу m. p.

Так доказана истинность ù$_x(P₃(x))®"_x"_y(P₁.(x, y)®(ùP₂(y))) при заданном наборе посылок и правил вывода.

Принцип резолюции

Если матрица формулы в результате приведения к виду ПНФ не будет содержать свободных переменных и сколемовских функций, то для вывода заключения применим алгоритм принципа резолюции исчисления высказываний. Однако если в результате приведения к виду ССФ аргументы атомов содержат сколемовские функции, то для поиска контрарных атомов необходимо выполнить подстановки термов вместо предметных переменных и получить новые формулы дизъюнктов, которые допускают их унификацию при формировании контрарных пар. Множество подстановок нужно формировать последовательно, просматривая каждый раз только одну предметную переменную.

Принцип резолюции может быть усилен упорядочением атомов в дизъюнкте и использо­ванием информации о резольвируемых атомах.

Упорядоченным дизъюнктом называется дизъюнкт с заданной последовательностью атомов. Атом P_j старше атома P_i в упорядоченном дизъюнкте тогда и только тогда, когда j>i. Например, в упорядоченном дизъюнкте (P₁ÚP₂ÚP₃ÚP₄) самым младшим считается атом P₁, а самым старшим - P₄. При наличии в упорядоченном дизъюнкте двух одинаковых атомов, по закону идемпотенции, следует удалить старший атом, сохранив на прежнем месте младший.

Другим усилением принципа резолюции является использование информации о резольвируемых атомах. Обычно при выполнении процедуры унификации происходит удаление резольвируемых атомов. Од­нако они несут полезную информацию. Поэтому вмес­то удаления резольвируемых атомов при унификации удаляют только старший атом, а младший - сохраняют в резольвенте, выделив какой-либо рамкой.

Если за обрамленным атомом в дизъюнкте не следует никакой другой атом, то его удаляют. Если за обрамленным атомом в дизъюнкте следует какой-либо необрамленный атом, то его следует оставить для последующего анализа. И, наконец, если последний необрамленный атом резольвенты унифицируется с отрицанием атома боковой ветви, то его следует обрамить и удалить вместе с литерой боковой ветви. Используя резольвенты на последующих этапах, можно получить обрамленными все атомы последней резольвенты.

Пример: существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один преподаватель не является невеждой. [1]

Пусть P₁(x):=” x – студент”, P₂(y):=”y – преподаватель”, P²₃(x, y):=”x любит y”, P₄(y):=”y - невежда”.

Формулы этого суждение имеют вид:

$_x(P₁(x)&"_y(P₂ (y)®P²₃(x; y)));

"_x(P₁(x) ®"_y(P₄ (y)®ùP²₃(x; y)));

"_y(P₂ (y)®ùP₄(y)).

· Преобразовать посылки и отрицание заключения в ССФ:

F₁=$_x(P₁(x)&"_y(P₂ (y)®P₃(x; y)))= $_x"_y(P₁(x)& (P₂ (y)®P₃(x; y)))= "_y(P₁(a)&(P₂ (y)®P₃(a; y)))= "_y(P₁(a)&(ùP₂ (y)ÚP₃(a; y)));

F₂="_x(P₁(x)®"_y(P₄ (y)®ùP₃(x; y)))="_x"_y(P₁(x)®(P₄ (y)®ùP₃(x; y)))=

"_x"_y(ùP₁(x)ÚùP₄ (y)ÚùP₃(x; y)));

F₃=ù"_y(P₂ (y)®ùP₄(y))=$_y(ù(ùP₂(y)ÚùP₄(y)))=$_y(P₂(y)&P₄(y))=P₂(b)&P₄(b).

· Выписать множество дизъюнктов:

K={P₁(a); (ùP₂ (y)ÚP₃(a; y)); (ùP₁(x)ÚùP₄ (y)ÚùP₃(x; y)); P₂(b); P₄(b)}.

· Выполнить унификацию и формирование резольвент:

P2(b)

P₂(b) Ú _xò^b(ùP₂ (y)ÚP₃(a; y))= Ú P₃(a; b);

 

P2(b)

Ú P₃(a; b)Ú_yò^b (ùP₁(x)ÚùP₄ (y)ÚùP₃(x; y))=

	P2(b)

= ÚP₃(a; b)Ú(ùP₁(x)ÚùP₄ (b)ÚùP²₃(x; b));

	P2(b)

Ú P₃(a; b)Ú_xò^a(ùP₁(x)ÚùP₄ (b)ÚùP²₃(x; b))=

	P2(b)
		P3(a; b)

= Ú ÚùP₁(a)ÚùP₄ (b);

	P2(b) )
		P3(a; b)

Ú ÚùP₁(a)ÚùP₄ (b) ÚP₁(a)=

ùP1(a)

P3(a; b)

P2(b)

= Ú Ú Ú ùP₄(b);

	P2(b) )
		P3(a; b)		ùP1(a)

Ú Ú Ú ùP₄(b) Ú P₄(b)= .

 

Процесс вывода заключения по принципу резолюции представлен графом на рис. 4.10.

Пример: “Преподаватели принимали зачеты у всех студентов, не являющихся отличниками. Некоторые аспиранты и студенты сдавали зачеты только аспирантам. Ни один из аспирантов не был отличником. Следовательно, некоторые преподаватели были аспирантами.” [1]

Пусть P₁(x):=”x – отличник”, P₂(x):=”x – аспирант”, P₃(x):=”x –студент”, P₄(x; y):=”x сдает зачет y”, P₅(x):=”x – преподаватель”.

Формулы этого суждения имеют вид:

"x(P₃(x)&ùP₁(x)®$y(P₅(y)&P₄(x, y)));

$x(P₂(x)&P₃(x)&"y(P₄(x, y)®P2(y)));

"x(P₂(x)®ùP₁(x)).

$x(P₅(x)&P₂(x)).

· Преобразовать посылки и отрицание заключения в ССФ:

F₁="x(P₃(x)&ùP₁(x)®$y(P₅(y)&P₄(x,y)))="x(ùP₃(x)ÚP₁(x)ÚP₅(f(x)))&

&(ùP₃(x)ÚP₁(x)ÚP₄(x; f(x)));

F₂=$x(P₂(x)&P₃(x)&"y(P₄(x;y)®P₂(y)))="y(P₂(a)&P₃(a)&

(ùP₄(a; y)ÚP₂(y)));

F₃="x(P₂(x)®ùP₁(x))="x(ùP₂(x)ÚùP₁(x));

F₄=ù$x(P₅(x)&P₂(x))= "x(ùP₅(x)ÚùP₂(x)).

· Выписать множество дизъюнктов:

K= {(ùP₃(x)ÚP₁(x)ÚP₅(f(x))); (ùP₃(x)ÚP₁(x)Ú P₄(x, f(x))); P₂(a); P₃(a);

(ùP₄ (a, y)ÚP₂(y)); (ùP₁(x)ÚùP₂(x)); (ùP₅(x)ÚùP₂(x))};

 

Эти операции показаны на графе 4.10.

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: