 |
Перемещения при изгибе балок
|
|
|
|
Рассмотрим балку жестко защемленную одним концом под действием силы Р на свободном конце (рис.13а). Координаты всех точек балки после деформации изменяются. При этом ось балки искривляется. Центр тяжести сечения «К» перемещается на плоскости. Проекцию этого перемещения по оси Y обозначим v – прогиб балки, проекцию по оси Z обозначим u – осевая составляющая. При справедливости гипотез о плоских сечениях и ненадавливании волокон сечение «К» повернется на угол 
. Таким образом (рис.13в), для того чтобы определить новое положение точки m в поперечном сечении «К», отстоящей от центра сечения на расстоянии y, нужно с помощью u и v определить положение точки «К ¢», показать сечение под углом и отложить все то же расстояние y.
Следовательно, знание трех компонент u, v, j для каждого сечения балки полностью определяет деформацию всей балки.
В обычных инженерных расчетах рассматриваются жесткие балки – деформации малы по сравнению их геометрическими размерами. Практика показывает, что осевые составляющие перемещения u на порядок меньше прогиба v. Поэтому u, по сравнению с v, пренебрегают, и рассматривают изгиб балки по расчетной схеме показанной на рис.13б, в которой центр сечения перемещается только по оси Y, а сечение поворачивается на угол j. Изогнутая ось балки называется упругой линией. Поворот сечения соответствует углу наклона касательной к оси Z.
Упругая линия представляет собой график функции 
, а угол наклона касательной равен первой производной от функции 
. (30)
Таким образом, для определения деформаций при изгибе достаточно знать аналитическое выражение для ординат упругой линии . Дифференциальное уравнение упругой линии балки
|
|
|
В процессе вывода формулы нормальных напряжений при изгибе была получена формула (14) для кривизны балки. По существу эта запись закона Гука: при изгибе внутренний силовой фактор – изгибающий момент, а деформация – кривизна упругой линии. Деформация прямо пропорциональна силовому фактору и обратно пропорциональна жесткости поперечного сечения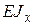 
.
В курсе высшей математики приводится выражение кривизны линии
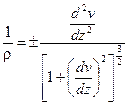(31)
рис. 13
Если ось Y направить вверх, то знаки изгибающего момента и знак кривизны совпадают, поэтому, подставляя (31) в (14) мы должны поставить знак плюс.
. (32)
Это точное дифференцированное уравнение упругой линии. Неизвестной является функция . Это нелинейное дифференциальное уравнение второго порядка с известной правой частью. Решение (32) в общем случае получить затруднительно, но для жестких балок прогиб мал по сравнению с пролетом, а угол наклона касательной 
поэтому в знаменателе квадратом этой величины по сравнению с единицей можно пренебречь. Теперь, дифференциальное уравнение превращается в линейное второго порядка с известной правой частью
. (33)
Интегрирование дифференциального уравнения упругой линии
Будем последовательно интегрировать (33):
(34)
Постоянные интегрирования 
находят из условий закрепления балки (рис.14).
В дальнейшем будем рассматривать балки постоянного сечения 
. Тогда вместо (33) можно записать
(35)
рис. 14
Выберем начало координат на левом конце балки (рис.15) и обозначим прогиб в начале координат 
, а угол поворота 
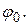Тогда постоянные будут иметь физический смысл. Запишем в соответствии с (34), учитывая (35):
рис. 15
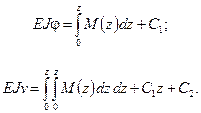(36)
При подстановке 
получим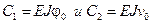 
. Теперь соотношения (36) можно записать в форме метода начальных параметров
(37)
В этом случае 
называют начальными параметрами.
Для стандартных нагрузок двукратное интегрирование соответствующих функций изгибающих моментов заранее выполнено и получены готовые формулы (рис.16).
|
|
|
рис. 16
Используя принцип независимости действия сил, запишем вместо (37)
(38)
Значок 
перед функцией называется прерывателем Бубнова, и означает, что при 
- это слагаемое равно 0, а при 
эту функцию нужно вычислять
(39)
Уравнение (38) называется универсальным уравнением упругой линии балки.
Рассмотрим пример применения этого уравнения (рис.17).
Определяем опорные реакции. В виду симметрии 
На балку действуют только сосредоточенные силы. Поэтому в уравнение упругой линии войдут слагаемые типа, показанного на рис.16б.
рис. 17
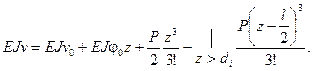
Определяем из условий закрепления:
1. 
2. 
(40)
Определим прогиб в середине балки
Для упругих деформаций характерно, что прогибы и углы поворота сечений балки прямо пропорциональны величине внешней нагрузки.
Метод начальных параметров позволяет получить аналитические выражения прогибов и углов поворота сечений 
на любом участке балки. Например (40) содержит по существу две разные функции на двух участках 
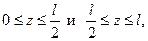записанные в одну строку с помощью прерывателя Бубнова.
При 
При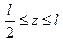 
, 
Во многих случаях нужно иметь способ нахождения компонентов перемещений конкретного сечения балки. Для обоснования такого способа применим принцип возможных перемещений.
Принцип возможных перемещений
Принцип возможных перемещений состоит в следующем: если некоторая механическая система под действием заданных сил находится в равновесии, то работа сил, приложенных к этой системе, на любых бесконечно малых возможных перемещениях равна нулю. Этот принцип является необходимым и достаточным условием равновесия любой механической системы. Он следует из общего уравнения механики Даламбера-Лагранжа.
Покажем применение этого принципа для вычисления опорной реакции в шарнирно подвижной опоре (рис.18а). Для этого превратим балку в механизм, отбросив связь, воспринимающую эту реакцию и заменив ее действие неизвестной силой 
(рис.18б). Возможным перемещением будет бесконечно малый поворот 
балки как абсолютно твердого тела относительно центра шарнирно неподвижной опоры В. Возможные перемещения должны соответствовать наложенным на систему связям.
|
|
|
рис. 18
При этом точки приложения сил и Р получает бесконечно малые перемещения по направлению этих сил (соответственно 
). Следовательно, и Р совершают работу на этих перемещениях. Такую работу в дальнейшем будем называть возможной. Сумму работ этих сил приравняем нулю.
(41)
Перемещения 
зависят от 
:
(42)
(43)
Подставив (42) и (43) в (41), получим
Отсюда, 
(44)
Получили тот же результат, который дает нам уравнение равновесия 
Доказано, что, применяя принцип возможных перемещений к упругим системам, вместо бесконечно малых возможных перемещений можно рассматривать малые, но конечные перемещения, которые возникают от конкретной нагрузки. Кроме того, возможные перемещения можно отсчитать не от деформированного состояния, а от начального, ненагруженного.
Часто за возможные перемещения для конкретной системы сил можно принять перемещения, вызванные другой системой нагрузок.
В дальнейшем обозначения компонент перемещений сечений будем снабжать двумя индексами – первый означает номер точки на оси балки сечения, которого перемещение определяется; второй означает номер системы сил, вызывающей это перемещение (
- прогиб точки i от системы сил с номером 
- тоже угол поворота сечения).
Для системы сил с номером 1 (рис.19а) перемещения от системы сил с номером 2 (рис.19б) можно считать возможными и наоборот, для сил в состоянии 2 возможными будут перемещения от сил в состоянии 1.
Можно подсчитать возможные работы этих внешних сил.
(45)
(46)
рис. 19
Возможная работа внутренних сил
Выделим двумя сечениями бесконечно малые участки балки в двух состояниях: в действительном 1 (рис.19а) и в состоянии 2, вызывающем возможные перемещения (рис.19б). В каждом из этих состояний в сечениях балки действуют внутренние силовые факторы М и Q. В дальнейшем не будем учитывать влияние поперечных сил Q, так как оно обычно мало по сравнению с влиянием М.
рис. 20
Покажем действие моментов отдельно для двух состояний (рис.20). Изгибающий момент в действительном состоянии является внутренним силовым фактором для балки, но для выделенного бесконечного малого элемента он является внешним моментом. Поэтому мы можем подсчитать элементарную возможную работу этого фактора, используя формулу типа (45), как работу внешних сил на возможных перемещениях, вызванных силами во втором состоянии (рис.19б).
|
|
|
Таким образом,
(47)
Для вычисления элементарной работы 
внутренних сил в выделенном элементе воспользуемся принципом возможных перемещений
(48)
Отсюда следует важный вывод
(49)
что возможная работа внутренних сил (сил упругости) равна возможной работе внешних сил, но с обратным знаком.
Подставляя (47) в (49) получим
(50)
Просуммировав возможную работу внутренних сил по всей балке, будем иметь 
(51)
где интегрирование проводится по всем участкам балки с постоянным законом для ординат эпюры изгибающих моментов.
Если действительное состояние имеет индекс i, а возможное состояние j, то 
(52)
Формула (52) показывает, что за действительное состояние можно принять любое из двух – тогда другое состояние будет считаться возможным для первого.
Формула Мора для определения перемещений при изгибе балок
Применяя принцип возможных перемещений для всей балки, запишем
(53)
Отсюда получим формулу для возможной работы внешних сил
(54)
Рассмотрим балку, показанную на рис.21а. Внешней нагрузкой является равномерно распределенная нагрузка q. Под действием этой нагрузки ось балки примет криволинейное очертание. Определим прогиб точки 1 в середине пролета 
. Для этого рассмотрим ту же балку (рис.21б), но по направлению приложим единичную силы 
Примем за действительное состояние 1 (рис.21б), для которого перемещения балки в состоянии q (рис.21а) будут возможными.
На основании принципа возможных перемещений, запишем сумму работ сил в состоянии 1 на возможных перемещениях состояния q.
рис. 21
В этом состоянии работу совершает сила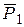 
Используя формулу (54), получим
или учитывая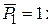 
(55)
Определим угол поворота сечения 2 на правой консоли 
. Для этого рассмотрим ту же балку, но по направлению искомого угла поворота приложим сосредоточенный момент 
(рис.21в). Примем за действительное состояние 2 (рис.21в), для которого перемещения балки в состоянии q (рис.21а) будут возможными.
На основании принципа возможных перемещений 
В состоянии 2на перемещениях в состоянии q совершает работу только сосредоточенный момент : 
Используя формулу (54), получим 
или учитывая , 
. (56)
Формулы (55) и (56) называются формулами Мора. В них 
- это ординаты эпюр моментов от единичных силовых факторов, приложенных в воображаемых состояниях 1 и 2 по направлению искомых перемещений 
|
|
|
Таким образом, по формулам Мора можно вычислить величину конкретного перемещения конкретного сечения балки.
Для этого нужно сделать следующее:
1. Построить эпюру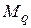 
в балке от заданной внешней нагрузки.
2. Рассмотреть балку в воображаемом состоянии, в котором по направлению искомого перемещения приложен единичный силовой фактор (если определяется прогиб, то прикладываются единичная сила, если определяется угол поворота сечения, то прикладывается сосредоточенный момент) и построить эпюру 
Черта сверху показывает, что момент определяется от единичной силы или единичного момента.
3. Перемножить соответствующие функции моментов на каждом участке, вычислить интегралы и результаты просуммировать по всем участкам балки.
Вычисление интеграла Мора. Правило Верещагина
Процедуру перемножения функций моментов в двух состояниях и последующего интегрирования произведения в пределах одного участка можно значительно упростить, если воспользоваться так называемым правилом Верещагина. На рис. 22 показаны фрагменты эпюр моментов в двух состояниях: действительном, в котором действует заданная нагрузка, и единичном (воображаемом). В действительном состоянии эпюра моментов может иметь криволинейное очертание, а в единичном – всегда прямолинейное.
рис. 22
Воспользуемся последним обстоятельством и продолжим прямую эпюры 
до пересечения с осью – отметим точку 01. Обозначим расстояние от точки 01 до текущей ординаты через Z. Тогда 
Приступим к вычислению определенного интеграла, считая поперечное сечение стержня в пределах одного участка постоянным.
Здесь введено обозначение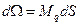 
- элементарная площадь эпюры. Последний интеграл по площади называется статическим моментом площади эпюры 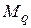относительно оси Y. Он численно равен произведению площади эпюры на расстояние от оси Y до центра тяжести этой площади. Таким образом, обозначив 
- координату центра тяжести эпюры 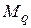относительно оси Y, а 
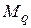- площадь эпюры , получим
где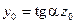 
- ордината эпюры – под центром тяжести эпюры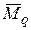 
.
Окончательно правило Верещагина формулируется следующим образом: для того, чтобы вычислить интеграл от произведения двух эпюр, нужно площадь криволинейной эпюры умножить на ординату прямолинейной под центром тяжести криволинейной и результат разделить на EJ.
Если обе эпюры прямолинейные, то площадь и центр тяжести можно вычислять у любой из них, а ординату – у другой.
Обычно криволинейность эпюры вызвана действием равномерно распределенной нагрузки. При этом всегда такую эпюру можно рассматривать как сумму прямолинейной эпюры, возникающей от концевых моментов, и параболического сегмента, имеющего вид эпюры моментов в однопролетной шарнирно опертой балке от равномерно распределенной нагрузки (рис.23).
рис. 23
Отклонение криволинейной эпюры в середине участка от линии соединяющей крайние ординаты 
и 
, называют стрелкой и обозначают f. От действия равномерно распределенной нагрузки q всегда
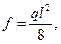(57)
а площадь – параболического сегмента
(58)
с центром тяжести посередине участка.
Прямолинейную часть эпюры можно, в свою очередь, рассматривать как сумму двух треугольных эпюр с центрами тяжести в соответствующей трети участка.
Расчет статически неопределимых балок
Статически неопределимыми балками называются балки, у которых число опорных реакций больше числа уравнений равновесия.
В задаче № 5 речь идет об один раз статически неопределимых балках. Примеры таких балок показаны на рис.24. Число опорных реакций на единицу больше числа уравнений равновесия. В схеме (рис.24в) кроме трех уравнений равновесия 
рис. 24
Можно составить четвертое - 
Расчет один раз статически неопределимых балок проводится в следующей последовательности:
1. Отбрасывается одна опорная связь и ее действие заменяется неизвестной реакцией 
При этом полученная схема балки должна быть геометрически неизменяемой и статически определимой. Эту схему балки в дальнейшем будем называть основной системой.
2. Для основной системы ставится условие, что реакция 
должна быть такой, что основная система должна деформироваться также как и заданная.
По направлению Х1 в основной системе отсутствует опорная связь, и может происходить перемещение по этому направлению. В заданной системе по этому направлению находится опорная связь и перемещение по направлению Х1 равно нулю. Следовательно, для определения Х1 нужно составить уравнение деформации, выражающее условие, что и в основной системе перемещение по направлению Х1 должно быть равно нулю. В соответствии с принципом независимости действия сил
(59)
здесь 
- перемещение по направлению Х1 в основной системе от силы 
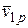- перемещение в основной системе по направлению Х1 от нагрузки.
Каждое из этих перемещений находится по формуле Мора
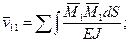(60)
(61)
Для этого строятся две эпюры: -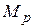 
от внешней нагрузки в основной системе, и 
- эпюра от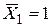 
в основной системе.
После определения Х1 строятся эпюры М и Q в основной системе как в статически определимой балке.
ЗАДАЧА № 3
Целью настоящей задачи является овладение навыками построения эпюр внутренних силовых факторов при изгибе балок и их расчет на прочность (подбор необходимого поперечного сечения). При этом необходимо усвоить сущность метода сечений, правило знаков для внутренних силовых факторов, порядок построения эпюр и методику вычерчивания приблизительного вида изогнутой оси изгибаемых элементов, а также суть расчета на прочность при изгибе.
Задачу будем решать в следующей последовательности:
1. Из уравнений равновесия (статики) найдем опорные реакции и проверим правильность их вычисления.
2. Установим количество характерных участков системы, в пределах каждого, из которых закон изменения изгибающего момента и поперечной силы неизменен. При этом границами участков будем считать точки, в которых происходит изменение характера приложения внешней нагрузки (появление сосредоточенных сил или моментов, начало или конец приложения распределенной нагрузки), а также изменение геометрических характеристик сечения балки или направления её оси.
3. Используя метод сечений, составим аналитические выражения для внутренних силовых факторов на каждом из участков в зависимости от текущей координаты вдоль оси балки.
4. Определим числовые значения внутренних силовых факторов в характерных сечениях на каждом из участков. Как правило, такими сечениями являются начало и конец участка, а также точка на оси балки, в которой изгибающий момент принимает экстремальное значение. (Эта точка требуется лишь в случаях, когда эпюра поперечной силы на рассматриваемом участке пересекает ось абсцисс, то есть Q принимает нулевое значение).
5. Строим эпюры внутренних силовых факторов, располагая их под расчетной схемой балки. При этом положительные значения ординат поперечных сил откладываем вверх, а отрицательные – вниз, в то время как эпюры изгибающих моментов строятся на растянутых волокнах. Знаки проставляются только на эпюрах поперечных сил.
6. Производим проверку правильности построения эпюр на основании дифференциальных зависимостей между изгибающим моментом и поперечной силой.
7. Изображаем примерный вид изогнутой оси балки.
8. Определяем опасное сечение, в котором действует наибольший по абсолютной величине изгибающий момент.
9. Из условия прочности при изгибе определяем наименьшее предельное значение момента сопротивления сечения.
10. Принимая во внимание конструктивные особенности и тип сечения, определяем характерные размеры (b и h в случае прямоугольного поперечного сечения или номер двутавра – в случае применения сортового проката).
Схема I. Консольная балка
1. При расчете консольной балки рекомендуется начинать ее обход со свободного конца и двигаться в сторону заделки. В этом случае опорные реакции на данном этапе расчета можно не определять, а их величины впоследствии взять с эпюр внутренних силовых факторов.
2. Поскольку в рассматриваемых нами задачах изгибная жесткость всех участков балки предполагается одинаковой, а ее ось – прямолинейной, то о начале каждого нового участка можно будет судить по изменениям характера внешней нагрузки. Так, двигаясь справа налево (в сторону заделки), мы видим силу P, что говорит о начале второго участка, и, далее, распределенную нагрузку q, которая продолжается до конца балки и заделки, тем самым определяя протяженность третьего, последнего участка (рис. 25а).
3. На протяжении каждого из указанных участков законы изменения изгибающего момента Mx и поперечной силы Qy будут неизменными и полученные нами уравнения будут справедливы для любой точки в их пределах. Таким образом, следует трижды рассечь балку (рис.25а) и в каждом случае выписать выражения для поперечной силы и изгибающего момента (рис.26).
Проводя последовательно сечения на первом, втором и третьем участках, рассмотрим равновесие правой отсеченной части, приложив к ней все действующие справа от сечения заданные нагрузки, и внутренние силовые факторы 
в положительном направлении.
рис. 25
Имеем:
Для первого участка (0≤ z 1 ≤ a):
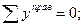Q y = 0 (силы отсутствуют)
рис. 26
Mx = - m
Для второго участка (0≤ z 2 ≤ b):
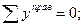Qy = - P
Mx = - m + P z 2
Для третьего участка (0≤ z 3 ≤ с):
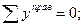Qy = - P + q z 3
Mx = - m + P(b + z 3 ) - q 
/2
Определим теперь значения Qy и M x в характерных сечениях (рассмотрим пока только точки начала и конца участков).
Первый участок:
Qy = 0
Mx = - m
Очевидно, что величины Qy и Mx от координаты z не зависят.
Второй участок:
При z = 0 Qy = - P Mx = - m
При z = b Qy = - P Mx = - m + Pb
Здесь Qy – константа (не зависит от координаты z в пределах второго участка), а Mx - наклонная прямая (параметр z входит в уравнение в первой степени).
Третий участок:
При z = 0 Qy = - P Mx = - m + P b
При z = c Qy = - P + q c Mx = - m + P(b + c) - q c 2/2
На этом участке сила Qy изменяется по линейному закону (её эпюра представляет собой наклонную линию), а момент Mx - по закону квадратной параболы (параметр z входит в уравнение во второй степени).
Для построения параболической кривой двух точек может оказаться недостаточно. Однако, при решении рассматриваемой задачи нас будут интересовать только максимальные (по абсолютной величине) значения момента в пределах каждого из участков, поэтому, если эпюра Mx на рассматриваемом участке не имеет экстремума, то наибольшим будет одно из граничных значений функции Mx , если же такой экстремум существует, то его определением мы займемся ниже.
4. Для наглядности предположим, что входящие в уравнения величины имеют следующие числовые значения:
a = 1 м, b = 2 м, c = 3 м, P = 10 кН, m = 10 кНм, q = 10 кН/м.
Подставляя их в ранее полученные аналитические выражения, будем иметь следующие результаты:
Таблица 3.1
| № участка | z, м | Qy, кН | Mx, кНм |
| 1 участок | z = 0 z = 1 | Qy = 0 Qy = 0 | Mx = -10 Mx = -10 |
| 2 участок | z = 0 z = 2 | Qy = -10 Qy = -10 | Mx = -10 Mx = +10 |
| 3 участок | z = 0 z = 3 | Qy = -10 Qy = +20 | Mx = +10 Mx = -5 |
Анализируя характер изменения поперечной силы на третьем участке, можно заметить, что ее эпюра начинается в отрицательной области значений Qy, а заканчивается в положительной и, следовательно, пересекает ось абсцисс. Определим координату z * этой точки, приравняв Qy нулю. Имеем:
Qy = - P + q z = 0, откуда P = q z и, окончательно, z * = P / q = 1 м.
Поскольку изгибающий момент и поперечная сила связаны дифференциальной зависимостью dMx / dz = Qy, а в рассматриваемой нами точке Qy =0, то изгибающий момент Mx принимает здесь экстремальное значение. Определим его, подставив z * = 1 в уравнение момента на третьем участке:
Mx = - m + P(b + z * ) - q z * 2/2 = 15 кНм.
и получим третью (промежуточную) точку для построения эпюры Mx.
5. Построим теперь эпюры поперечных сил и изгибающих моментов. Для этого отложим перпендикулярно к оси абсцисс (для каждой эпюры это линии, параллельные оси балки) в удобном для пользования масштабе вычисленные значения Qy и Mx для граничных и промежуточных сечений участков и соединим концы полученных ординат линиями, соответствующими законам изменения Qy и Mx. При этом положительные ординаты эпюры Qy будем откладывать вверх, а отрицательные – вниз от оси абсцисс; ординаты же эпюры Mx будем откладывать со стороны растянутых волокон. При вычерчивании параболических участков эпюр изгибающих моментов форма линии эпюры должна соответствовать “ правилу паруса ”, что применительно к эпюрам, построенным на растянутых волокнах легко интерпретировать графически (см. рис. 27)
Рис. 27
то есть выпуклость линии эпюры соответствует направлению действия распределенной нагрузки. Знание этого правила особенно полезно при вычерчивании участков эпюр изгибающих моментов по двум точкам.
После завершения построений на эпюре Qy нужно проставить знаки, на эпюре же Mx их обычно не ставят (см. рис. 25б и 25в).
Полезно отметить, что из построенных нами эпюр Mx и Qy теперь можно легко определить численные значения внутренних силовых факторов в заделке (опорную реакцию и момент), не определенные нами в начале решения задачи. Так, из рис. 25б находим R = +20 кН (↑), а из рис. 25в – изгибающий момент M оп = -5 кНм (против часовой стрелке).
6. Проверим теперь правильность построения эпюр Mx и Qy и их соответствие друг другу. Из зависимости dMx / dz = Qy становится очевидным, что порядок линии, описывающей закон изменения изгибающего момента всегда на единицу выше, чем порядок линии, описывающей эпюру поперечных сил. Следовательно, на участках балки между эпюрами внутренних силовых факторов должны существовать следующие зависимости:
| Изгибающий момент | Квадратная парабола | Наклонная прямая | Константа |
| Поперечная сила | Наклонная прямая | Константа | Отсутствует |
В местах приложения сосредоточенных нагрузок (сил и моментов) на эпюрах соответствующих им внутренних силовых факторов должны иметь место скачки, равные им по величине. Так, приложенная внешняя сила P будет вызывать скачок на эпюре Qy, а наличие сосредоточенного момента m будет говорить о скачке на эпюре Mx.
Нелишне еще раз убедиться и в наличие экстремумов на эпюре моментов, а также в соответствии их положений нулевым ординатам на эпюре Qy.
Как видим, в нашем случае все указанные свойства в эпюрах присутствуют.
7. Построим теперь изображение примерного вида изогнутой оси балки. Поскольку наши построения носят приближенный характер, то основой для проведения такой линии будут являться следующие положения:
a) Кривизна балки на участках должна соответствовать расположению эпюр изгибающих моментов. Так, если для какого-либо участка эпюра Mx построена на нижних волокнах (в данном случае они растянуты), то кривизна балки должна иметь вид, приведенный на рис. 28а. Если же эпюра моментов расположена на верхних волокнах (теперь они растянуты), то участок балки примет форму, представленную на рис. 28б.
| 
|
| Рис. 28а | Рис.28б |
Как видим, на левом рисунке растянуты (удлиняются) нижние волокна, а на правом – верхние.
b) В точке заделки вне зависимости от величины изгибающего момента поворот сечения отсутствует, следовательно, линия изогнутой оси балки должна выходить под прямым углом (в данном случае, к вертикали).
c) Участки с разными знаками кривизны упругой линии должны сопрягаться плавной линией (без изломов), а сечение, в котором кривизна меняет знак и которое называется точкой перегиба, должно быть показано на чертеже.
Построенная с учетом вышесказанного упругая линия консольной балки изображена на рис.25г.
8. Подбор размеров поперечного сечения осуществляем по методу допускаемых напряжений, из которого следует, что в рассмотрение следует принимать лишь то сечение балки, в котором действует наибольший по абсолютной величине изгибающий момент. Однако при этом нужно иметь в виду, что данный прием можно использовать только в случае, когда изгибная жесткость балки EJx на всем ее протяжении одинакова, то есть вся балка изготовлена из одног
|
|
|
