Методы распознавания в пространстве параметров

 

Методы распознавания (разделения) диагнозов в пространстве параметров основываются на том, что каждый объект описывается набором (комплексом) диагностических параметров, которые принимаются в качестве компонентов n -мерного вектора. Поэтому каждому объекту можно поставить в соответствие точку в пространстве параметров, в которой находится конец этого вектора. Считается, что точки, отображающие одинаковые технические состояния (диагнозы), группируются в одной области параметров, т.е. образуют «компактное множество». Следовательно, каждому диагнозу соответствует некоторая область в пространстве параметров. В такой трактовке задача постановки диагноза сводится к выработке формализованного метода, позволяющего определить, в какой области пространства параметров находится конец вектора, компоненты которого соответствуют комплексу диагностических параметров, измеренных у контролируемого объекта.

Прежде, чем переходить непосредственно к самим методам распознавания, рассмотрим некоторые свойства пространственных параметров.

1. Как отмечалось ранее (см. главу 1), каждый объект (его техническое состояние) может характеризоваться комплексом (набором) диагностических признаков или параметров, которые в равной степени могут приниматься в качестве компонент n -мерного вектора. В зависимости от того, что используется для описания объекта (параметры или признаки), компоненты этого вектора могут быть дискретными или непрерывными.

Дискретные компоненты встречаются тогда, когда техническое состояние объекта описывается диагностическими признаками или их разрядами.

В качестве непрерывных компонент могут выступать непосредственно диагностические параметры (давление Р, температура t, расход топлива G _т и др.).

2. Если для описания технического состояния объекта используются простые бинарные (двухразрядные) признаки, то компоненты вектора могут выражаться двоичными числами, т.е. сочетанием 0 и 1. Например, в трехмерном пространстве техническое состояние объекта может быть определено следующим вектором: у = {0, 1, 1}.

На рис. 5.3 изображены трехмерное пространство признаков и вектор с указанными координатами. При таком описании объектов диагностики любое из технических состояний (диагнозов) будет находиться в вершине единичного куба. Таким образом, если число признаков n, то каждый i -й диагноз D_i будет являться вершиной единичного n -мерного куба.

 

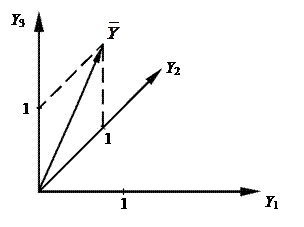
Рис. 5.3 Трехмерное пространство признаков

 

3. Областью диагноза D_i называется множество точек пространства признаков, которое соответствует техническим объектам, обладающим состоянием D_i. Запись у Î D_i имеет двоякий смысл: во-первых, это означает, что объект находится в состоянии D_i; во-вторых, что точка, описываемая вектором у, попадает в область D_i.

При использовании понятий пространства диагностических параметров (признаков) и определении каждого состояния в виде области диагноза задача диагностики может решаться путем отыскания уравнения разделяющей функции, или разделяющей плоскости. Уравнение разделяющей функции выводится через так называемые дискриминантные функции.

Дискриминантные функции

Пусть в n -мерном пространстве параметров содержатся точки, принадлежащие различным диагнозам D ₁, D ₂, …, D_i, …, D_m. Для каждой области пространства параметров (диагноза) D_i определим скалярную функцию f_i () = f_i (y _l, y ₂, …, y_k, …, y_n).Функция f_j ()называется дискриминантной функцией диагноза D_i, если она отвечает условию

f_i () > f_j () при Î D_i, где i ¹ j, a j = 1, 2, …, m.

То есть дискриминантная функция f_i ()принимает для точек области D_i (диагноза D_i) n -мерного пространства параметров наибольшее значение по сравнению с дискриминантными функциями других диагнозов. Линейная дискриминантная функция диагноза D_i будет иметь вид

f_i () = l _{i 1}·y₁ + l _{i 2}· y ₂ + … + l _in ·y _n + l _{i ( n + 1)}, (5.11)

где l _{i 1}, …, l _in, l _{i ( n + 1)} – весовые коэффициенты линейной дискриминантной функции f_i ().

Поясним это положение на следующем примере. Пусть мы имеем два диагноза D ₁ и D ₂. Техническое состояние объектов диагностики характеризуется двумя параметрами у ₁ и y ₂. Пусть для этих диагнозов заданы некоторые функции, которые определяются следующими выражениями:

f ₁(y ₁, у ₂) = l₁₁· y ₁ + l₁₂· y ₂ + l₁₃,

(5.12)

f ₂(y ₁, у ₂) = l₂₁· y ₁ + l₂₂· y ₂ + l₂₃.

Функция f ₁(y ₁, у ₂) называется дискриминантной функцией диагноза D ₁, если она всегда больше f ₂(y ₁, у ₂) при условии, что объект относится к диагнозу D ₁, т.е. если = { у ₁, у ₂} Î D ₁. Функция f ₂(y ₁, у ₂) называется дискриминантной функцией диагноза D ₂,если она всегда больше f ₁(y ₁, у ₂) при условии, что объект относится к диагнозу D ₂,т.е. если = { у ₁, у ₂} Î D ₂.

Разделяющая функция

Допустим, что области диагнозов D ₁и D ₂имеют общую границу, как это изображено на рисунке 5.4.

 

Рис. 5.4 Области диагнозов с общей границей

 

Существование общей границы у областей диагнозов определяет равенство на этой границе дискриминантных функций, т.е. на общей границе областей f ₁(y ₁, у ₂) = f ₂(y ₁, у ₂). При ={ у ₁, у ₂} Î D ₁ выполняется условие f ₁(y ₁, у ₂) >> f ₂(y ₁, у ₂), а при = { у ₁, у ₂} Î D ₂ – следующее условие:
f ₁(y ₁, у ₂) << f ₂(y ₁, у ₂).

На основе этих свойств дискриминантной функции вводится понятие разделяющей функции, которая в нашем случае определится таким образом:

f () = f (y ₁, у ₂) = f ₂(y ₁, у ₂) – f ₁(y ₁, у ₂). (5.13)

Последнее выражение определяет линейную разделяющую функцию для двух диагнозов в двухмерном пространстве диагностических параметров, которая представляет собой прямую линию. Подставив выражения (5.12) в формулу (5.13), получим

f () = (l₂₁ – l₁₁)· y ₁ + (l₂₂ – l₁₂)· y ₂ + (l₂₃ – l₁₃).

Последнее выражение после несложных преобразований можно записать в виде

f () = l₁ · y₁ + l₂ · y₂ + l₃,

где l _i – весовые коэффициенты разделяющей функции.

При количестве параметров больше двух линейная разделяющая функция описывает разделяющую плоскость. В случае двух диагнозов при n -мерном пространстве параметров выражение для линейной разделяющей функции будет иметь следующий вид:

f () = l₁ · y ₁ + l₂ · y ₂ + … + l_I · y_i + … + l _n · y_n + l_{(n + 1)}, (5.14)

а весовые коэффициенты этой функции определятся соотношением

l _i = (l_{2 i} – l_{1 i}).

С использованием понятия разделяющей функции решающее правило будет выглядеть следующим образом:

f (y ₁, y ₂) > 0 Þ y Î D ₁,

(5.15)

f (y ₁, y ₂) < 0 Þ y Î D ₂.

В ряде случаев для повышения надежности распознавания вводят зону неопределенности, или так называемый «порог чувствительности» e (рис. 5.5).

 

Рис. 5.5 Области диагнозов с зоной неопределенности

 

Тогда решающее правило будет выглядеть следующим образом:

если f (y ₁, y ₂) e Þ D ₂ , если f (y ₁, y ₂) £ e Þ D ₁,

где e – пороговое значение разделяющей функции.

Если выполняется условие – e < f (y ₁, y ₂) < e, то принимается решение об отказе от диагноза.

Все сказанное выше позволяет сделать заключение о том, что в общем случае для двух диагнозов D_i и D_j разделяющая функция определяется через дискриминантные функции этих диагнозов, т.е. в виде

f () = f_i () – f_j ().

Методы распознавания в пространстве параметров, которые строятся на основе линейных разделяющих функций, называются линейными методами распознавания (разделения).В свою очередь, диагнозы, которые возможно разделить с помощью этих методов, называются линейно разделимыми.

Как следует из выражения (5.14), знание весовых коэффициентов полностью определяет разделяющую функцию. Комплекс весовых коэффициентов можно представить как вектор с числом компонент n + 1. Поэтому если вектор весовых коэффициентов = (l₁, l₂, …, l _{k +1}) определен, то решать задачу распознавания диагнозов можно путем вычисления значений разделяющей функции при тех значениях измеренных параметров, которые получены из опыта. После расчета значения разделяющей функции следует воспользоваться решающим правилом, заданным выражением (5.15).

Таким образом, основной задачей в такой постановке является поиск вектора весовых коэффициентов. Прежде чем переходить к поиску этого вектора, проанализируем его свойства. Анализ проведем на основе следующих соображений.

Выше отмечалось, что вектор весовых коэффициентов задается n + 1 компонентами, т.е. описывается в (n + 1)-мерном пространстве. Дополним n -мерный вектор диагностических параметров еще одним параметром (компонентом) у_{n + 1} = 1, т.е. дополненный вектор диагностических параметров запишем в следующем виде:

_* = { y ₁, y ₂, … y_k, …, y_n, y_{n + 1}}.

При таком дополнении разделяющую функцию f (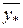)можно представить в виде скалярного произведения вектора весовых коэффициентов и дополненного вектора диагностических параметров :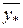

f ( _*) = _*. (5.16)

Это скалярное произведение описывает уравнение плоскости в
(n + 1)-мерном пространстве (гиперплоскость) и в развернутом виде записывается следующим образом:

f ( _*) = l₁ · y ₁ + l₂ · y ₂ + … + l _k · y_k + … + l _n · y_n + l _{n + 1}· y_{n + 1} = 0. (5.17)

Последние два выражения позволяют сформулировать два свойства вектора весовых коэффициентов и разделяющей гиперплоскости, которые будут использоваться при их определении:

1. Вектор весовых коэффициентов и гиперплоскость перпендикулярны друг другу.

2. В дополненном пространстве признаков разделяющая гиперплоскость всегда проходит через начало координат.

Поясним на простейшем примере указанные свойства.

Пусть объект диагностики может находиться в одном из двух диагнозов D ₁ или D ₂. Техническое состояние объекта характеризуется диагностическим параметром у_i (рис. 5.6).

 

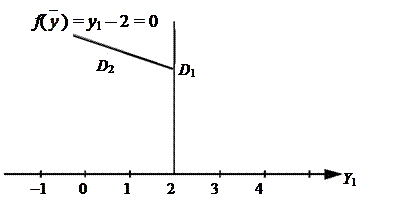
Рис. 5.6 Разделяющая функция в основном пространстве признаков

 

Разделяющая функция описывается уравнением f () = y ₁ – 2 = 0, а решающее правило будет выглядеть следующим образом:

если у ₁ < 2 Þ D ₂,

если у ₁ > 2 Þ D ₁.

Введем дополнительный параметр у ₂ = 1. Тогда уравнение разделяющей функции f ()определится следующим выражением: f () = y ₁ – 2 у ₂ = 0 (рис. 5.7), а выражение для вектора весовых коэффициентов будет выглядеть следующим образом: = {1, – 2}.

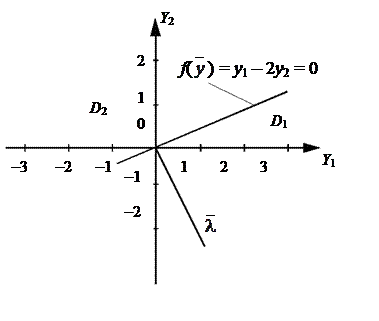
Рис. 5.7 Разделяющая функция в дополненном пространстве признаков

 

Полученные соотношения и рисунок 5.7 свидетельствуют о том, что разделяющая функция в дополненном пространстве диагностических признаков проходит через начало координат, а вектор весовых коэффициентов перпендикулярен к ней.

Нахождение вектора весовых коэффициентов разделяющей функции

Рассмотрим случай, когда объект диагностики может находиться в двух диагнозах D ₁ и D ₂, а его техническое состояние характеризуется двумя диагностическими параметрами y ₁ и у ₂. Решение поставленной задачи в двухмерном варианте позволяет использовать наглядную графическую иллюстрацию, а в то же время перенос полученных результатов на многомерный случай не вызывает затруднений.

Решение рассматриваемой задачи возможно при наличии некоторой априорной информации о значениях диагностических параметров объектов, находящихся в обоих технических состояниях. Пусть известны значения диагностических параметров y ₁ и у ₂ для числа М ₁ технических объектов (образцов), находящихся в диагнозе D ₁, и для числа М ₂ образцов, находящихся в диагнозе D ₂. Эти образцы изображены на рисунке 5.8 в виде точек, куда попадают концы соответствующих векторов. Совокупность векторов, попадающих в область диагноза D ₁, называется обучающей выборкой диагноза D ₁. Совокупность векторов, попадающих в область диагноза D ₂, называется обучающей выборкой диагноза D ₂.

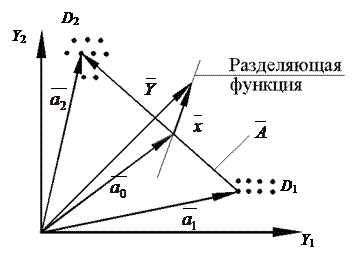
Рис. 5.8 Построение разделяющей функции в двухмерном пространстве параметров

 

Введем понятие «средний вектор», или «эталон», для каждого из диагнозов D ₁ и D ₂. В векторной форме для диагноза D ₁ эталон определится следующим выражением:

,

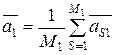где 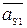– s -й вектор, конец которого попадает в область диагноза D ₁.

Очевидно, что в скалярной форме нахождение эталона сводится к определению средних значений по каждой координате.

Соответственно, для диагноза D ₂ в векторной форме эталон определяется следующим выражением:

,

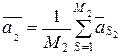где 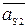– s -й вектор, конец которого попадает в область диагноза D ₂.

Определим вектор 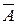, соединяющий концы эталонов. Из рисунка 5.8 видно, что этот вектор можно определить как разность эталонов:

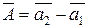. (5.18)

Без доказательств примем, что разделяющая функция проходит через середину этого вектора и она перпендикулярна к нему. Это соответствует физическому смыслу разделяющей функции, поскольку она должна быть равноудалена от обеих областей диагнозов – и от D ₁, и от D ₂. Определим среднюю точку на векторе 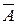и соединим ее с началом координат. Вектор 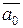,соединяющий начало координат с этой точкой (рис. 5.8), определится следующим соотношением:

,

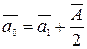или, после соответствующих подстановок и преобразований, следующим соотношением:

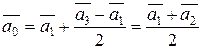. (5.19)

Рассмотрим вектор 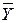, конец которого лежит на прямой, принятой за разделяющую функцию (рис. 5.8). Поскольку конец вектора 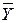лежит на разделяющей функции, то, если подставить значение его координат в уравнение разделяющей функции, уравнение разделяющей функции примет значение, равное нулю. Этот вектор можно представить как сумму вектора 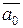и вектора , лежащего на разделяющей функции, т.е.

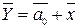или . (5.20)

Поскольку вектор лежит на разделяющей функции, то его скалярное произведение с вектором равно нулю: 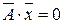. Производя соответствующую подстановку и используя выражения (5.18) и (5.20), получим

.

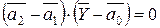Раскрывая скобки и производя замену 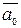через выражение (5.19), мы придем к следующему соотношению:

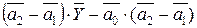= . (5.21)

Для выполнения непосредственных вычислений необходимо перейти от векторной формы записи уравнения к скалярной, для чего вместо векторов в формулу (5.21) нужно поставить их координаты. Для нашего двухмерного случая векторы, представленные в формуле (5.21), определим через их координаты в следующем виде:

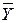={ y ₁, y ₂}; 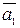= { a ₁₁, a ₁₂}; 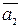= { a ₂₁, a ₂₂}.

Подставив координаты векторов в формулу (5.21), получим следующее выражение:

(5.22)

где а ₁² и а ₂² – квадраты модулей соответствующих векторов.

Сопоставляя полученное выражение с выражением (5.17) для разделяющей функции в дополненном пространстве параметров, получим выражения для вычисления компонентов весового вектора в рассматриваемом нами примере:

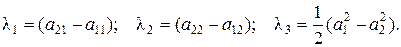
Полученные результаты несложно перенести на n -мерное пространство параметров. Для этого представим рассматриваемые векторы 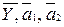через их координаты (компоненты) в n -мерном пространстве параметров:

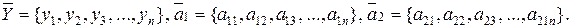
Проведя рассуждения, аналогичные двухмерному случаю, получим выражение для разделяющей функции (гиперплоскости), справедливое для n -мерного случая:

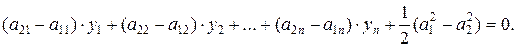(5.23)

Данное уравнение соответствует уравнению разделяющей плоскости, записанному в общем виде. Из этого уравнения определим выражения для компонентов весового вектора:

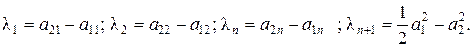(5.24)

Знание компонентов весового вектора позволяет проводить процедуру диагностирования.

Алгоритм определения координат весового вектора
и постановки диагноза на его основе

Постановка задачи. Пусть имеются диагнозы D ₁ и D ₂,каждый из которых описывается набором векторов.

1. Определяют эталоны (средние векторы) для каждого диагноза:

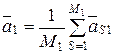и ,

а точнее их компоненты а ₁₁, а ₁₂, …, а _{1 n}, a ₂₁, a ₂₂, …, a _{2 n}.

2. Определяют модули эталонных векторов:

а ₁² = а ₁₁² + а ₁₂² + … + а _{1 n} ² и а ₂² = а ₂₁² + а ₂₂² + … + а _{2 n} ².

3. Определяют компоненты весового вектора (весовые коэффициенты разделяющей функции):

4. Проводят диагностирование. Предъявленный объект представляется вектором своих параметров 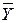= { у ₁, у ₂, у ₃, …, y_n }.Далее определяют скалярное произведение .Если > 0, то объект относят к D ₂;если < 0, то объект относят к D ₁.

Применение разделяющих функций или плоскостей можно реализовать просто в том случае, если эти функции линейны и количество диагнозов не превышает двух.

Для решения задач в случае большего количества диагнозов или при нелинейной постановке чаще используются метрические методы распознавания в пространстве параметров.

Метрические методы распознавания в пространстве параметров

Эти методы также основаны на представлении (описании) диагностируемого объекта вектором в n -мерном пространстве параметров. Базовым понятием в этих методах является понятие метрика пространства диагностических параметров. Поэтому рассмотрим первоначально это понятие. Начнем с наиболее распространенной метрики – евклидовой.

Евклидова метрика. Пусть имеются две точки в пространстве параметров а и у. Точка а описывается в пространстве координатами а ₁, а ₂,..., a_j,..., а_n, а точка у описывается в пространстве координатами y ₁, y ₂,...,
y_j,..., y_n. Если расстояние между этими точками определяется соотношением

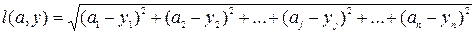, (5.25)

то такое пространство называется евклидовым. Величина, определенная по формуле (5.25), называется евклидовом расстоянием или евклидовой метрикой. В евклидовом пространстве его метрика обладает рядом свойств. Приведем эти свойства:

l (a, y) ³ 0, l (a, y) = l (y, a), l (a, a) = 0,

(5.26)

l (a, c) £ l (a, b) + l (b, c)

В ряде диагностических задач целесообразнее использовать так называемое обобщенное расстояние порядка k или обобщенную метрику порядка k. Обобщенная метрика порядка k для n -мерного пространства параметров определяется следующим соотношением:

,

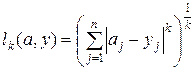где k может принимать значения от 1 до ¥. При k = 2 последнее выражение определяет евклидову метрику.

Наиболее часто применяется евклидова метрика, которая записывается без корня:

. (5.27)

Рассмотренные выше метрики применимы только в том случае, если векторы диагностических параметров (признаков) имеют одинаковую размерность, т.к. при вычислении метрик используется операция сложения разностей различных параметров. Такое пространство параметров называют однородным или изотропным.

Если диагностические параметры (признаки) имеют разные единицы измерения, то пространство параметров неоднородно. При использовании такого пространства параметров производится нормализация координат путем введения весовых коэффициентов:

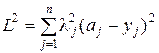, (5.28)

где l _j – весовой коэффициент по j -й координате.

Чаще всего в качестве нормализующего весового коэффициента по j -й координате используют величину, обратную среднеквадратическому отклонению диагностического параметра y_j, т.е. l _j = 1/s _j. В этом случае весовой коэффициент l _j имеет определенный физический смысл. Чем меньше рассеивание диагностического параметра или признака, тем больше его вклад в метрику, т.е. тем больше его значимость для диагностики технического состояния объекта.

Диагностирование с помощью метрик называется диагностированием по расстоянию между диагнозами в пространстве параметров. Диагностирование по расстоянию разделяют на следующие методы:

– метод диагностирования по расстоянию до эталона;

– метод диагностирования по расстоянию до множества.

Диагностирование по расстоянию до эталона

В этом методе отнесение предъявленного для распознавания объекта к одному из диагнозов совершается по наименьшему расстоянию до эталона, характеризующего этот диагноз. В качестве эталона для некоторого диагноза принимается «типичный» для данного диагноза объект. Наиболее естественно определить «типичный» объект как некий средний для данного диагноза объект.

Пусть имеется диагноз D_i. Известно, что М_i объектов попадают в область диагноза D_i и каждый из этих объектов характеризуется своим вектором параметров a_is (где s изменяется от 1 до М_i). С учетом сказанного выше в качестве эталона примем объект, который описывается средним векторомпараметров а_i (где 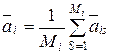). Компоненты этого вектора по каждой из координат определяются как средние значения соответствующих координат всех М_i объектов, попадающих в диагноз D_i. Например, по j -й координате компонент а_i^j для среднего вектора 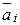определится следующим образом:

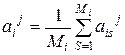, (5.29)

где а_is^j – значение j -й координаты (j -гo параметра) s -гo объекта, входящего в диагноз D_i. После определения эталона можно проводить процедуру диагностирования.

Алгоритм диагностирования по расстоянию до эталона

1. Для каждого i -гo диагноза по априорным данным определяют эталоны, которые задаются средними векторами 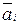. Координаты средних векторов рассчитывают по формуле (5.29).

2. Для неизотропных пространств параметров определяют средние квадратичные значения s _ij для i -го диагноза по j -й координате (j -му диагностическому параметру).

3. Проводят расчет расстояний (метрики) между вектором, характеризующим предъявленный к диагностированию объект, и векторами эталонов.

4. Объект относят к тому диагнозу, с которым имеет минимальное расстояние или минимальную метрику: L_i = min.

Необходимо отметить, что надежность распознавания диагноза тем выше, чем меньше расстояние L_i по сравнению с другими. Сопоставление этих расстояний можно провести следующим образом. Введем величину, обратную этому расстоянию, т.е. 1/ L_i. Сопоставление расстояний L_i ведется по следующему отношению

,

где М – число известных диагнозов; i и m – текущие номера диагнозов. Вычисленная по этому отношению величина эквивалентна вероятности появления i -го диагноза, т.к. .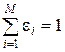

Диагностирование по расстоянию до множества

В этом методе оценивается расстояние не до одного эталона, а до всех точек, попадающих в данную область диагноза D_i. Причем в качестве оценки расстояния до диагноза чаще всего используется один из двух достаточно простых критериев.

В качестве первого критерия используется минимальное расстояние от конца вектора диагностических параметров, характеризующего диагностируемый объект, до конца вектора диагностических параметров, характеризующего объект, принадлежащий диагнозу D_i. В этом случае алгоритм распознавания строится следующим образом.

Алгоритм диагностирования по минимальному расстоянию

1. Определяется расстояние 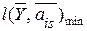от предъявленного объекта, характеризуемого вектором 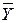, до всех объектов данного диагноза D_i, характеризуемых собственными векторами диагностических признаков :

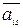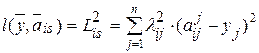. (5.30)

2. Для диагноза D_i. определяют минимальное расстояние .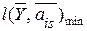

3. Подобную процедуру выполняют для всех известных диагнозов.

4. Проводят сравнение выявленных минимальных расстояний по всем диагнозам. Объект относят к тому диагнозу, с которым он имеет наименьшее расстояние из этих минимальных расстояний.

В качестве второго критерия используют среднее расстояние от конца вектора, характеризующего диагностируемый объект, до области диагноза D_i. В этом случае алгоритм распознавания строится следующим образом.

Алгоритм диагностирования по среднему расстоянию

1. Определяется расстояние 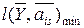от предъявленного объекта, характеризуемого вектором 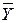, до всех объектов данного диагноза D_i, характеризуемых собственными векторами диагностических признаков a_is в соответствии с формулой (5.30).

2. Для каждого диагноза D_i определяют среднее значение расстояний до диагностируемого объекта:

l _ср 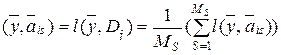. (5.31)

3. Объект относится к тому техническому состоянию (к тому диагнозу), с которым он имеет минимальное среднее расстояние.

Напомним, что применение методов распознавания предполагает обладание некоторым количеством априорной информации. Так, использование методов разделения в пространстве параметров требует, чтобы каждый из диагнозов был предварительно описан первоначальной выборкой, в которую входили бы не менее десяти объектов.

 

5.5 Контрольные вопросы к главе 5

 

1. В каких случаях используется детерминистский подход при решении задач распознавания диагнозов?

2. На чем основан процесс распознавания диагноза по методу Байеса?

3. В чем отличие методов принятия статистических решений от Байесовского подхода?

4. При каких условиях применяются «метод минимального риска» и «метод минимального числа ошибочных решений»?

5. Когда применяется метод «максимального правдоподобия» и «метод минимакса»?

6. На чем основаны методы распознавания в пространстве параметров?

7. Чем отличается метод диагностирования по расстоянию до эталона от диагностирования по расстоянию до множества?

 

ГЛАВА 6 ЗАДАЧИ ПРОГНОЗИРОВАНИЯ
ТЕХНИЧЕСКОГО СОСТОЯНИЯ И ПРИНЦИПЫ
ПОСТРОЕНИЯ ДИАГНОСТИЧЕСКИХ СИСТЕМ

Основные положения

 

В предыдущих главах были изложены основы технической диагностики, т.е. науки об определении состояния технических систем в настоящий момент времени. Между тем выше отмечалось, что при оценке состояния техники необходимо решать три типа задач, а именно задачи генезиса, диагноза и прогноза.

Важность решения задач прогноза связана с тем, что использование методов прогнозирования технического состояния для объектов направлено на оценку остаточных ресурсов, на обоснование режимов технической эксплуатации, на выбор периодичности и объемов технического обслуживания и ремонта, а также на выявление потенциальных отказов и обеспечение принятия решения до возникновения фактического отказа.

К сожалению, в настоящее время задачи прогнозирования в практическом плане разработаны слабо, но, учитывая их важность, рассмотрим основные положения прогнозирования [2, 8, 13, 16, 19, 23].

Задачу прогнозирования технического состояния объектов будем рассматривать как задачу прогнозирования потенциальных неисправностей или отказов. В теоретическом плане для решения прогностических задач необходимо:

– сформулировать задачу прогноза конкретной неисправности (или отказа) и определить связанные с этой неисправностью диагностические параметры;

– накопить необходимые исходные данные об изменении выбранных диагностических параметров до настоящего времени;

– разработать (выбрать) модель развития технического состояния по данной неисправности (модель изменения диагностических параметров при развитии дефекта);

– выбрать метод прогнозирования и определить параметры модели прогноза технического состояния;

– произвести расчет и по результатам расчета принять решение.

При такой постановке задачи прогнозирование технического состояния объектов контроля базируется на выявлении тенденции изменения (тенденции развития) диагностических признаков и параметров. Исходными данными для прогнозирования являются полученные в процессе эксплуатации значения диагностических признаков и параметров, зарегистрированные при различных значениях наработки изделия. Важнейшей характеристикой исходных данных является минимальная длина интервала предыстории, на котором проявляются закономерности изменения прогнозируемого явления. Свойства этой априорной информации в значительной степени определяют выбор той или иной модели для формализованного описания развития неисправности и изменения диагностических параметров.

Формирование прогнозной модели является довольно сложной самостоятельной задачей. При этом без учета физической сущности прогнозируемого явления не обойтись.

Определение законов изменения физических процессов основано на одном из фундаментальных постулатов, сформулированных К. Шенноном [22]. Суть постулата в том, что основные закономерности, наблюдаемые в прошлом, будут сохраняться и в будущем.

Сложность и разнообразие прогнозируемых физических явлений привели к созданию большого количества методов прогнозирования. Выбор и подгонка того или иного метода прогнозирования является довольно сложной задачей. На правильный выбор метода в первую очередь влияет количество априорной информации о прогнозируемом явлении, ее достоверность, адекватность прогнозируемому явлению.

Итак, в процессе прогнозирования можно выделить четыре основных этапа: сбор и подготовка исходных данных, идентификация прогнозируемого явления, выбор метода прогнозирования, собственно прогнозирование.

Из всего сказанного выше следует, что качество исходных данных имеет огромное значение при определении результатов прогнозирования. Рассмотрим некоторые особенности изменения диагностических параметров, которые могут оказать влияние на процедуру прогнозирования [10].

Если зарегистрировать изменени

⇐ Предыдущая1234567

Поделиться:

Воспользуйтесь поиском по сайту: