Аналитический способ решения задачи 1

y' = 2 ty.

Методом разделения переменных найдем:

y' / y = 2 t

Будем интегрировать от 0 до t_i, тогда согласно правилам интегрирования имеем:

Полученное аналитическое решение характеризуется тем, что оно является абсолютно точным, но если уравнение окажется сколько-нибудь сложным, то решение не будет найдено вовсе. Аналитический путь решения не универсален.

Численный способ решения задачи 1

Численный способ решения предполагает, что расчет будет вестись по формуле Эйлера на ряде последовательных шагов. На каждом шаге решение имеет свою ошибку (см. рис. 10.2), поскольку на каждом шаге кривая заменяется прямым отрезком.

При алгоритмической реализации расчет реализуется циклом, в котором изменяется t (счетчик t) и y:

t:= t + Δt y:= y + 2 · t · y · Δt

Блок-схема при реализации метода на компьютере показана на рис. 10.5.

Рис. 10.5. Блок-схема реализации метода Эйлера

В реализации Стратум запись будет выглядеть так (наличие символа «~» при t):

t:= t + Δt y:= y + 2 · ~t · y · Δt

Будем искать значение y рассмотренного ранее примера в численном виде на промежутке от T = 0до T = 1. Возьмем число шагов n = 10, тогда шаг приращения Δ t составит: Δ t = (1 – 0)/ n = (1 – 0)/10 = 0.1.

Таблица 10.1. Численный расчет уравнения методом Эйлера и сравнение результата с точным решением на каждом шаге

i ti yi = yi – 1 + y'i – 1 · Δ t y'i = 2 ti · yi Δ yi = y'i · Δ t yi + 1 = yi + Δ yi y точн. = exp(ti 2)   0.0             0.1   0.2 0.02 1.02 1.0101   0.2 1.02 0.408 0.0408 1.0608 1.0408   0.3 1.061 0.636 0.0636 1.1246 1.0942   0.4 1.124 0.900 0.0900 1.2140 1.1735   0.5 1.214 1.214 0.1214 1.3354 1.2840   0.6 1.336 1.603 0.1603 1.4963 1.4333   0.7 1.496 2.095 0.2095 1.7055 1.6323   0.8 1.706 2.729 0.2729 1.9789 1.8965   0.9 1.979 3.561 0.3561 2.3351 2.2479   1.0 2.335 4.669 0.4669 2.8019 2.7183

Обратите внимание на то, что рассчитанное численно значение (y_{i + 1}) отличается от точного (y _точн.), и погрешность (разница столбцов y_{i + 1} и y _точн.) в процессе расчета нарастает подобно тому, как было показано на рис. 10.4.

Теперь подсчитаем относительную погрешность σ для расчетного значения y (1), полученного численно, в сравнении с теоретическим точным y _теор. по следующей формуле:

σ = (1 – y _расч./ y _теор.) · 100%

и сравним σ при различных значениях Δ t.

Если будем менять значение шага Δ t, например, уменьшать шаг, то относительная погрешность расчета тоже будет уменьшаться. Вот что получится при вычислении значения y (1) с разными значениями шага (см. табл. 10.2).

Таблица 10.2. Зависимость погрешности расчета от размера шага Δ t

Δ t y расч.(1) y теор.(1) σ 1/10 2.3346 2.7183 14% 1/20 2.5107 2.7183 8% 1/100 2.6738 2.7183 2%

Как видим, с уменьшением шага приращения Δ t уменьшается величина относительной погрешности, а значит, повышается точность расчета.

Обратите внимание, что изменение шага в 10 раз (с 1/10 до 1/100) ведет к изменению величины ошибки примерно тоже в 10 раз (с 14% до 2%). При изменении шага в 100 раз ошибка примерно уменьшится тоже в 100 раз. Иными словами размер шага и ошибка для метода Эйлера связаны линейно. Хотите уменьшить в 10 раз ошибку — уменьшайте в 10 раз шаг и увеличивайте соответственно в 10 раз количество вычислений. Этот факт в математике принято обозначать символом ε = O (Δ t), а метод Эйлера называют методом первого порядка точности.

Поскольку в методе Эйлера ошибка достаточно велика и от шага к шагу накапливается, а точность пропорциональна количеству вычислений, то метод Эйлера обычно применяют для грубых расчетов, для оценки поведения системы в принципе. Для точных количественных расчетов применяют более точные методы.

Примечания

1. Каждый численный метод обладает точностью, поскольку результат отличается от теоретического. Точность метода зависит от величины шага. Различные методы имеют различную точность. Порядок зависимости точности от величины шага обозначают как O (h). У метода Эйлера первый порядок точности, зависимость ошибки от величины шага линейна.

2. Если при уменьшении шага предел y_n стремится к значению y _теор., то говорят, что метод обладает сходимостью. Исследователей интересует скорость сходимости метода.

3. Метод должен быть устойчив. Устойчивость связана с некоторой критической величиной шага. При проявлении неустойчивости наблюдается полное искажение качественной картины расчета, «разболтка» результата.

4. При выборе метода рекомендуется сначала добиться устойчивости, а внутри области устойчивости — сходимости результата. Устойчивость обеспечивает качественную картину. Сходимость обеспечивает количественный результат (см. также рис. 10.10).

Изложенное в пп. 1-4 поясним на примере.

Пример. Пусть

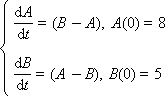
Качественно это уравнения описывают процесс теплообмена между двумя телами, температуры которых в некоторый момент времени обозначим как A и B. Вообще A и B — переменные, меняющиеся во времени t. Найти поведение системы означает, что надо найти, как будут меняться температуры A (t)и B (t).

Интуитивно ясно, что при начальной разнице температур A = 8 и B = 5 температуры тел постепенно со временем должны выровняться, так как более горячее тело будет отдавать энергию более холодному, и его температура будет уменьшаться, а более холодное тело будет принимать энергию от более горячего, и его температура будет увеличиваться. Процесс теплообмена закончится (то есть изменения прекратятся) тогда, когда температуры двух тел станут одинаковыми.

Проведем несколько расчетов поведения A (t) и B (t) с разной величиной шага Δ t.

Будем брать различную величину шага Δ t и находить соответствующие значения A и B во времени по следующим формулам Эйлера:

A ^нов. = A ^пред. + (B ^пред. – A ^пред.) · Δ t,
B ^нов. = B ^пред. + (A ^пред. – B ^пред.) · Δ t.

Расчет при Δ t = 2 (табл. 10.3).

Таблица 10.3. Изменение температур тел при численном расчете с шагом 2

№ шага t A B                       –7

Наблюдается явление «разболтки» (см. рис. 10.6). Неустойчивое решение. Из физических соображений очевидно, что так вести себя два тела в процессе теплообмена не могут.

Рис. 10.6. Система ведет себя качественно неверно. Решение неустойчиво

Расчет при Δ t = 1 (табл. 10.4).

Таблица 10.4. Изменение температур тел при численном расчете с шагом 1

№ шага t A B

Наблюдается поведение решения системы на границе устойчивости (см. рис. 10.7).

Рис. 10.7. Система ведет себя качественно неверно. Решение находится на грани устойчивости

Расчет при Δ t = 0.5 (табл. 10.5).

Таблица 10.5. Изменение температур тел при численном расчете с шагом 0.5

№ шага t A B           0.5 6.5 6.5   1.0 6.5 6.5

Решение устойчиво, соответствует правильной качественной картине (см. рис. 10.8). Температуры тел постепенно сближаются, становятся со временем одинаковыми. Но решение пока имеет большую погрешность.

Рис. 10.8. Система ведет себя качественно правильно. Решение (поведение системы) имеет большую погрешность

Расчет при Δ t = 0.1 (табл. 10.6).

Таблица 10.6. Изменение температур тел при численном расчете с шагом 0.1

№ шага t A B           0.1 7.7 5.3   0.2 7.46 5.54   0.3 7.27 5.73   0.4 7.12 5.88   0.5 7.00 6.00

Решение устойчиво. Решение более точно (см. рис. 10.9).

Рис. 10.9. Система ведет себя качественно верно. Количественно решение более точно

Роль изменения величины шага иллюстрирует рис. 10.10.

Рис. 10.10. Связь величины шага расчета с устойчивостью метода и его точностью (на примере)

Построение модели динамической системы в виде дифференциальных уравнений и расчет ее методом Эйлера Выполним построение модели динамической системы в виде дифференциальных уравнений и расчет ее методом Эйлера на примере. Пример. Пусть исследуется система двух материальных тел A и B с различными теплофизическими свойствами (см. рис. 11.1). Система контактирует с опорой с температурой Tп и помещена во внешнюю среду с температурой Tc. Интересует протекание процесса изменения температур тел. Рис. 11.1. Система взаимодействующих тел в задаче теплопроводности Как видно, в процессе жизни в системе изменяются (могут измениться) четыре показателя: температуры тел A, B, Tс, Tп. Значит, мы имеем дело с четырьмя переменными, зависящими от времени (поскольку переменные меняют свои значения со временем). Введем эти переменные: X 1(t), X 2(t), X 3(t), X 4(t). Для построения математической модели данной системы отразим процесс теплопередачи в виде графа зависимостей (рис. 11.2). Рис. 11.2. Граф зависимости переменных системы Если иметь в виду переменные X 1(t), X 2(t), X 3(t), X 4(t), то граф будет выглядеть так, как показано на рис. 11.3. Рис. 11.3. Граф зависимости переменных модели Стрелка от A к B обозначает изменение температуры X 2(t) объекта B под влиянием объекта A. Понятно, что ряд стрелок (например, от B к Tс, от A к Tп и др.) отсутствует, то есть нет влияния одних параметров на другие: тело B не в состоянии сколько-нибудь существенно нагреть открытую атмосферу, а тело A — массивную и потенциально бесконечную опору. Строго говоря, такое влияние есть, но оно настолько ничтожно, что разумно им пренебречь. Поскольку переменных четыре, то нам необходимо, как минимум, четыре закона, описывающих их изменение. В общем виде, учитывая, от каких переменных зависит каждый показатель, получим: для тела A имеем зависимость температуры X 1(t) от температуры тела B и температуры атмосферы Tс: d X 1(t)/d t = f 1(X 2(t), X 3(t)); для тела B имеем зависимость температуры X 2(t) от температуры тела A, температуры атмосферы Tс и опоры Tп: d X 2(t)/d t = f 2(X 1(t), X 3(t), X 4(t)). Стрелки, входящие в соответствующий кружок, указывают на количество влияющих параметров, а то, откуда они исходят, определяет конкретные названия переменных. Для среды закон имеет вид: X 3(t) = const, то есть, температура атмосферы Tс не зависит от остальных составляющих данной системы и, соответственно, не изменяется. Для опоры закон имеет вид: X 4(t) = const, то есть, температура опоры Tп не зависит от остальных составляющих данной системы и, соответственно, не изменяется. Система законов в первом приближении сформирована. Остается определить их конкретный вид: раскрыть, что из себя представляют значения выражений f 1 и f 2. Так как мы имеем дело с системой, зависящей от своего прошлого поведения на каждом последующем шаге, то мы применили для ее описания дифференциальные уравнения. Основной динамический закон для описания изменения переменной (уравнение движения) имеет вид: d X (t)/d t = w (x (t), y (t), z (t), …). Физический смысл записи таков. Производная в левой части уравнения, по определению, показывает, насколько изменяется X с изменением времени t. В инженерии подобное изменение называется скоростью, темпом, тенденцией. Итак, чтобы записать закон изменения переменной в дифференциальных уравнениях, надо указать скорость изменения переменных. Сначала рассмотрим первое уравнение: d X 1(t)/d t = f 1(X 1(t), X 2(t), X 3(t)). Появление X 1 в правой части означает, что скорость изменения температуры зависит от собственного состояния тела. Что такое f 1? — это функция, связывающая переменные X 1, X 2, X 3 между собой. То есть, переменные соединены друг с другом знаками операций. Взгляните на граф на рис. 11.3. Какие пары переменных взаимодействуют? Стрелки соединяют X 1(t) с X 2(t), X 1(t) с X 3(t), то есть имеет место два процесса, влияющих на скорость. Мы рассматриваем процессы теплообмена тел. Известно, что два процесса теплообмена независимы, то есть не управляют друг другом. Значит, результаты двух процессов можно складывать, они как бы накладываются друг на друга. Действительно, тепло, переданное от одного тела, складывается с теплом, переданным от другого. Таким образом, имеем: d X 1(t)/d t = g 1(X 1(t), X 2(t)) + g 2(X 1(t), X 3(t)). Раскроем структуру оставшихся выражений g 1 и g 2. Очень удобно, что g 1 никак не зависит от g 2и может рассматриваться отдельно. Такое разделение возможно, так как процессы g 1 и g 2 независимы. Процесс g 1 идет независимо от того, идет или нет процесс g 2. Независимость процессов и линейность (аддитивность) выражений — понятия связанные. Итак: так как процессы g 1 и g 2 независимы, то забудем на некоторое время о g 2. Какой знак нужно поставить между X 1(t) и X 2(t) в выражении g 1? Возможные варианты: X 1(t) + X 2(t); X 2(t) – X 1(t); X 1(t) – X 2(t); X 1(t) · X 2(t); X 1(t) / X 2(t); X 2(t) / X 1(t); X 1(t) ^ X 2(t); X 2(t) ^ X 1(t) и далее более сложные, например, X 12(t) · cos(X 2(t))/exp(X 1(t)). Исследователь начнет с наиболее простых выражений — природа построена просто. И только если простейшие выражения не удовлетворяют исследователя, он переходит к более сложным вариантам описания.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: