Задача синтеза (обратная задача)

Цель задачи синтеза — нахождение экстремума функции результата. Когда анализ закончен и построены функции, графики, таблицы, когда объект (его свойства и поведение) исследован во всех вариантах возможных входных воздействий, имеет смысл найти среди всего этого многообразия откликов наилучший. Обычно выход — цель функционирования системы, и логично принять, что цель должна принимать лучшие из всех возможных значений, потому имеет смысл найти такие значения входных параметров U, при которых выходной показатель Y примет свое наилучшее значение (экстремум). При этом под экстремумом может подразумеваться как минимум, так и максимум зависимости Y (U). Чтобы найти экстремум, модель включают в контур (см. рис. 20.11) с некоторым алгоритмом A, осуществляющим автоматическое управление входом U и построенным так, что в результате его работы производится поиск такого входного воздействия U на модель M, при котором она выдает наилучший выходной результат.

Рис. 20.11. Схема решения обратных задач (синтез)

Существуют различные алгоритмы поиска оптимума функции Y = M (U). Упомянем три из них (подробно эти и другие методы вы будете изучать в дисциплине «Системный анализ и исследование операций»).

1. Метод перебора. Алгоритм метода перебора представлен на рис. 20.12. Этот метод обеспечивает поиск глобального экстремума, но расточителен к вычислительным ресурсам, так как просматривает все возможные входные значения U с определенным шагом H и выбирает наилучший среди всех выходных результатов Y (см. рис. 20.13). Наилучшее из встреченных Y сохраняется и уточняется в ячейке R, значение U при этом значении Y сохраняется по ходу алгоритма в ячейке Z. Кроме этого имеется риск пропустить нужную точку, «перешагнув» через нее из-за слишком большого размера шага H.

Рис. 20.12. Алгоритм перебора, примененный к решению задачи синтеза — поиск наилучшего U для максимизации Y

2.

Рис. 20.13. Характерный рисунок поиска экстремума функции Y = M(U) методом перебора

3. Метод деления шага пополам. Этот метод более экономичен по отношению к методу перебора, так как анализирует по ходу движения, в каком направлении происходит улучшение (увеличение или уменьшение) функции Y = M (U) и старается двигаться именно в этом направлении. Если при этом попутно обнаруживается, что тенденция во время движения изменилась (уменьшение Y сменилось на его увеличение или наоборот), то алгоритм (рис. 20.14) разворачивается обратно (то есть меняет знак приращения входного сигнала на обратный) и снова идет в нужную сторону, но шаг при этом уменьшается вдвое. Это позволяет подойти к точке экстремума с малым значением шага поиска, что лучше локализует результат (см. рис. 20.15).

Рис. 20.14. Алгоритм деления шага пополам, примененный к решению задачи синтеза — поиск наилучшего U для максимизации Y

4.

Рис. 20.15. Характерный рисунок поиска экстремума функции Y = M(U) методом деления шага пополам

5. Метод градиента. Метод, алгоритмическая реализация которого представлена на рис. 20.16, использует свойства гипотетической кривой Y = M (U), а именно тот факт, что по направлению производной p, вычисленной на основе двух рядом стоящих точек, можно определить, в какую сторону уменьшается (увеличивается) значение цели Y и двигаться сразу в нужную сторону (см. рис. 20.17). Такая стратегия существенно сокращает время поиска. Недостатком алгоритма является то, что производная может перестать меняться в области локального экстремума, и глобальный экстремум такой алгоритм не найдет.

Рис. 20.16. Алгоритм поиска экстремума методом градиента, примененный к решению задачи синтеза

6.

Рис. 20.17. Характерный рисунок поиска экстремума функции Y = M(U) методом градиента

Задачу настройки модели мы уже подробно обсуждали в лекциях 02—08 (см. лекцию 02), и останавливаться на ней мы уже не будем. Это способы построения собственно самой модели.

Тренажеры

Этот класс задач, использующих модели, применяют для выработки навыков обучения у управляющего персонала. К тренажерам близки компьютерные игры. Управление моделью в данном случае осуществляет человек-оператор, который наблюдает за выходом модели (см. рис. 20.18). Воздействуя на вход модели, оператор старается добиться нужного выходного результата, и в процессе этих действий получает необходимые навыки по управлению, которые затем может перенести на реальный объект. На рис. 20.19 показан примерный вид алгоритма реализации тренажера на базе модели.

Рис. 20.18. Схема использования модели в тренажерах

 

Рис. 20.19. Типичный вид алгоритма реализации тренажера

Разумеется, тренажер должен обладать качествами наблюдаемости и управляемость. То есть оператор в принципе может и должен судить о качестве своих действий, только наблюдая какие-то важные для себя результаты на выходе. И модель должна быть построена таким образом, чтобы можно было достичь хотя бы в принципе искомых результатов какими-то входными воздействиями на нее (управляемость).

Параллельно с моделью может функционировать система оценки деятельности оператора, а также блок автоматического определения наилучших решений, которые могут в определенных режимах (например, режим обучения или подсказки) помогать оператору (см. рис. 20.20). Для этого к модели следует подключить экспертную систему, дающую рекомендации оператору в затруднительных для него случаях.

Рис. 20.20. Схема построения тренажера с функциями экспертной системы

Для выработки устойчивых навыков у персонала в процессе тренажа в информацию вносят дополнительные помехи, имитирующие реальные сложности, возникающие на объекте. Можно вносить помехи на входе (нарушается управляемость), на выходе (нарушается наблюдаемость) или в переменные состояния модели (см. рис. 20.21). Следует различать равнодушно действующие помехи и целенаправленное противодействие. В первом случае речь идет о случайном процессе, мешающем оператору достичь цель. Случайная помеха может, как увеличить свое значение, так и равновероятно уменьшить его, то есть чаще всего среднее значение помехи на большом интервале времени равно нулю. Во втором случае речь идет о целенаправленной дезинформации оператора (среднее ее действия не равно нулю).

Для тренажа играет большую роль среднее значение и дисперсия величины помех, которые постепенно наращивают с ростом опыта оператора.

Рис. 20.21. Схема тренажера, дополненного генератором помех

Теперь обсудим вопросы снятия и использования системных характеристик, то есть таких характеристик, которые представляют свойства системы в целом. Напомним, важнейшими понятиями для системы являются управление, помехи, цель. Системная характеристика должна связать эти понятия вместе. Методика снятия характеристик такова.

Выделяем переменные U (вход, управление) и Y (выход, цель) для исследования.

Закрепляем остальные X в виде некоторого фиксированного значения. Для каждого U из диапазона допустимых значений U _min ≤ U ≤ U _max наблюдаем и фиксируем в табл. 20.2 результат Y.

Таблица 20.2. Зависимость результата от управления при отсутствии действия помехи. Точки зависимости сняты как результат работы имитационной модели

Q (помехи) U (управление) Y (результат)

На графике (см. рис. 20.22) строим точку с координатами (U, Y). В результате ряда экспериментов получается кривая Y (U), которая показывает зависимость выхода от входа, цели от управления.

Обычно, если мы имеем дело моделью, отражающей сложную систему достаточно реально, с большой степенью адекватности, зависимость Y (U) должна иметь примерно такую зависимость, как показано на рис. 20.22.

Рис. 20.22. Примерный вид зависимости показателя цели от управления (ресурса), характерный для сложных систем

ВНИМАНИЕ! Здесь приведены наиболее общие рассуждения, вид кривой может быть весьма различным!!!! На рис. 20.22 четко видны следующие закономерности.

1. Кривая исходит из нуля. Если не управлять, не вкладывать ресурс, не стараться, сама по себе система вряд ли выдаст тот результат, который нужен вам, который вам полезен.

2. Кривая нелинейна. Сначала (при малых значениях U) приложение даже небольших усилий ведет к хорошему приросту показателя цели. Далее (при больших значениях U) каждый очередной успехΔ Y дается все большим усилием Δ U. Говоря математическим языком, сначала при малых U, производная Δ Y /Δ U имеет большое значение, с ростом U ее значение уменьшается.

3. Кривая имеет затухающий характер, стремится к насыщению. Действительно, представьте, если вы вложите огромные значения ресурса (например, затратите на рекламу своей автозаправки в Перми миллиард рублей), то вряд ли получите соответствующую прибыль. Прибыль Y на этом участке U будет лимитирована уже другими факторами (наличие желающих заправиться будет не больше, чем число автовладельцев в городе, например). Реальная система рано или поздно, но выходит на определенный «предел», на «упор», насыщение.

Выделите на объекте переменную помеха Q. По смыслу эта переменная должна мешать достигать цель и не зависеть от воли владельца, управлять ею он не может.

Далее следует сменить значение Q (ранее мы считали, что оно равно 0) и провести все описанные выше действия снова (см. табл. 20.3).

Таблица 20.3. Зависимость результата от управления при повышенном уровне действия помехи. Точки зависимости сняты как результат работы имитационной модели

Q (помехи) U (управление) Y (результат)

И снова построить по таблице экспериментов график (см. рис. 20.23). Очевидно, что при действии возмущений Q график 2 пройдет ниже, чем график 1, поскольку наличие помехи означает, что для достижения того же эффекта Y следует приложить больше управляющих усилий U. Заметим, что менять Q во время изменения U не следует, чтобы четко видеть связь Y именно от U.

Рис. 20.23. Примерный вид зависимости показателя цели от управления (ресурса) и возмущения, характерный для сложных систем

Важно!!! Если помеха все-таки во время снятия кривой Y (U) меняется самопроизвольно, а это бывает в том случае, когда помеха носит случайный характер, то следует для нанесения одной точки на график сначала провести несколько экспериментов при одном и том же U, а потом усреднить результат Y. Средняя величина более достоверна, чем одна из случайных реализаций. Сколько надо провести экспериментов для усреднения, чтобы обеспечить заданную точность ответа, мы обсудим с вами позднее в лекции 21 и лекции 34.

Снова увеличьте Q и снова проведите эксперименты, и снова получите новую таблицу (см. табл. 20.4) и новый график (см. рис. 20.23) — Y (U). В результате вы получите семейство кривых 1-2-3, отражающих зависимость цели, как от управления, так и от помехи.

Таблица 20.4. Зависимость результата от управления при высоком уровне действия помехи. Точки зависимости сняты как результат работы имитационной модели

Q (помехи) U (управление) Y (результат)

Снятие экспериментальных данных закончено. Теперь в любой момент при заданных Q и Y, используя графики 1, 2, 3, вы можете предсказать результат — необходимый для достижения цели Y уровень управления U. Такая задача, напомним, называется обратной.

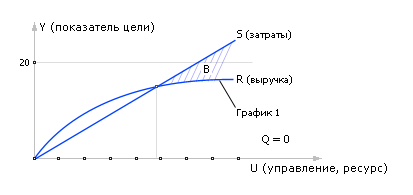
Теперь, используя снятые зависимости, полезно найти наилучшие решения среди множества возможных. Для этого на каждом графике 1, 2, 3 дополнительно построим линию затрат S (spending), так как управление всегда чего-то стоит, и чем больше вы используете этот ресурс, тем больше приходится за это платить. Наклон этой линии указывает на цену ресурса (см. рис. 20.24).

Рис. 20.24. Совмещенные графики выручки от реализации цели (выручка) и затрат на ее достижение

Примем для примера, что цена на ресурс неизменна и не зависит от того, сколько вы его используете (хотя, заметим, что бывают оптовые скидки).

Допустим, мы должны максимизировать цель Y. Тогда кривая R (receipts), выраженная в стоимостных единицах, символизирует выручку, а линия S (spending), выраженная в тех же стоимостных единицах символизирует затраты. Если вычесть из выручки затраты, то есть вычесть по точкам один график из другого (R – S), то получим в итоге прибыль P (profit): P = R – S. А именно, то, как прибыль зависит от управления (см. рис. 20.25).

Рис. 20.25. Суммарный график прибыли, полученной (выручка минус затраты) в зависимости от величины управления (ресурса) U. Наилучшее решение — максимум прибыли — точка Е1, наилучшее управление — U1

Очевидно, что зона B (bankrupt) — зона банкротства, точка N (null) — точка «ничего не делай и нечего не имей» и точка E ₁ (extremum) — зона наибольшей прибыли. Получить прибыли больше, чем Y ₁ при этом уровне, помех Q не удастся. Эта точка символизирует тот простой факт, что результат, достигнутый любой ценой, не окупает чрезмерных усилий по его достижению, «все хорошо в меру». Любые управляющие воздействия, даже большие, чем U ₁, дают худший результат.

Аналогично найдем точку E на остальных графиках 2, 3 — E ₂, E ₃.

Рис. 20.26. Графики прибыли, в зависимости от величины управления (ресурса) U и возмущения Q. Точки наилучших решений Еi — максимум прибыли. Соответствующие им наилучшие управления — Ui

Сведем все точки E со всех трех графиков на один новый график (см. рис. 20.27).

Рис. 20.27. Итоговый график наилучших решений E по критерию прибыли Y в зависимости от величины управления (ресурса) U и возмущений Q

Мы получили замечательную зависимость «кривая оптимальных значений цели Y в зависимости от наилучших решений U при заданном уровне помех Q», по которой можно узнать оптимальные прилагаемые управляющие усилия, необходимые для того, чтобы достичь наилучшего в этих условиях результата. Назовем эту кривую «взаимозависимость цели, управления и помех».

На графике видно, что наибольшая достижимая возможная прибыль уменьшается от точки к точке с увеличением величины помехи — точка E смещается. Например, возможен случай, если помехи очень сильны, а ресурс имеет фиксированную цену, то, возможно, что лучше ничего не делать.

Учтя вышесказанное и возвращаясь к лекции 01 (рис. 1.9—1.10), еще раз обратим внимание, что построение и использование моделей в составе программных продуктов — перспективное новое направление в проектировании программного обеспечения. Изучение оптимальных вариантов действий по управлению предприятием должно быть обеспечено инструментами моделирования.

Статистическое моделирование

Статистическое моделирование — базовый метод моделирования, заключающийся в том, что модель испытывается множеством случайных сигналов с заданной плотностью вероятности. Целью является статистическое определение выходных результатов. В основе статистического моделирования лежит метод Монте-Карло. Напомним, что имитацию используют тогда, когда другие методы применить невозможно.

Метод Монте-Карло

Рассмотрим метод Монте-Карло на примере вычисления интеграла, значение которого аналитическим способом найти не удается.

Задача 1. Найти значение интеграла:

На рис. 21.1 представлен график функции f (x). Вычислить значение интеграла этой функции — значит, найти площадь под этим графиком.

Рис. 21.1. Определение значения интеграла методом Монте-Карло

Ограничиваем кривую сверху, справа и слева. Случайным образом распределяем точки в прямоугольнике поиска. Обозначим через N ₁ количество точек, принятых для испытаний (то есть попавших в прямоугольник, эти точки изображены на рис. 21.1 красным и синим цветом), и через N ₂— количество точек под кривой, то есть попавших в закрашенную площадь под функцией (эти точки изображены на рис. 21.1 красным цветом). Тогда естественно предположить, что количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) по отношению к площади испытуемого прямоугольника. Математически это можно выразить так:

Рассуждения эти, конечно, статистические и тем более верны, чем большее число испытуемых точек мы возьмем.

Фрагмент алгоритма метода Монте-Карло в виде блок-схемы выглядит так, как показано на рис. 21.2.

Рис. 21.2. Фрагмент алгоритма реализации метода Монте-Карло

Значения r ₁ и r ₂ на рис. 21.2 являются равномерно распределенными случайными числами из интервалов (x ₁; x ₂) и (c ₁; c ₂) соответственно.

Метод Монте-Карло чрезвычайно эффективен, прост, но необходим «хороший» генератор случайных чисел. Вторая проблема применения метода заключается в определении объема выборки, то есть количества точек, необходимых для обеспечения решения с заданной точностью. Эксперименты показывают: чтобы увеличить точность в 10 раз, объем выборки нужно увеличить в 100 раз; то есть точность примерно пропорциональна корню квадратному из объема выборки:

Схема использования метода Монте-Карло при исследовании
систем со случайными параметрами

Построив модель системы со случайными параметрами, на ее вход подают входные сигналы от генератора случайных чисел (ГСЧ), как показано на рис. 21.3. ГСЧ устроен так, что он выдает равномерно распределенные случайные числа r _рр из интервала [0; 1]. Так как одни события могут быть более вероятными, другие — менее вероятными, то равномерно распределенные случайные числа от генератора подают на преобразователь закона случайных чисел (ПЗСЧ), который преобразует их в заданный пользователем закон распределения вероятности, например, в нормальный или экспоненциальный закон. Эти преобразованные случайные числа x подают на вход модели. Модель отрабатывает входной сигнал x по некоторому закону y = φ (x) и получает выходной сигнал y, который также является случайным.

 

Рис. 21.3. Общая схема метода статистического моделирования

В блоке накопления статистики (БНСтат) установлены фильтры и счетчики. Фильтр (некоторое логическое условие) определяет по значению y, реализовалось ли в конкретном опыте некоторое событие (выполнилось условие, f = 1) или нет (условие не выполнилось, f = 0). Если событие реализовалось, то счетчик события увеличивается на единицу. Если событие не реализовалось, то значение счетчика не меняется. Если требуется следить за несколькими разными типами событий, то для статистического моделирования понадобится несколько фильтров и счетчиков N_i. Всегда ведется счетчик количества экспериментов — N.

Далее отношение N_i к N, рассчитываемое в блоке вычисления статистических характеристик (БВСХ) по методу Монте-Карло, дает оценку вероятности p_i появления события i, то есть указывает на частоту его выпадения в серии из N опытов. Это позволяет сделать выводы о статистических свойствах моделируемого объекта.

Например, событие A совершилось в результате проведенных 200 экспериментов 50 раз. Это означает, согласно методу Монте-Карло, что вероятность совершения события равна: p _A = 50/200 = 0.25. Вероятность того, что событие не совершится, равна, соответственно, 1 – 0.25 = 0.75.

Обратите внимание: когда говорят о вероятности, полученной экспериментально, то ее называют частостью; слово вероятность употребляют, когда хотят подчеркнуть, что речь идет о теоретическом понятии.

При большом количестве опытов N частота появления события, полученная экспериментальным путем, стремится к значению теоретической вероятности появления события.

В блоке оценки достоверности (БОД) анализируют степень достоверности статистических экспериментальных данных, снятых с модели (принимая во внимание точность результата ε, заданную пользователем) и определяют необходимое для этого количество статистических испытаний. Если колебания значений частоты появления событий относительно теоретической вероятности меньше заданной точности, то экспериментальную частоту принимают в качестве ответа, иначе генерацию случайных входных воздействий продолжают, и процесс моделирования повторяется. При малом числе испытаний результат может оказаться недостоверным. Но чем более испытаний, тем точнее ответ, согласно центральной предельной теореме.

Заметим, что оценивание ведут по худшей из частот. Это обеспечивает достоверный результат сразу по всем снимаемым характеристикам модели.

Пример 1. Решим простую задачу. Какова вероятность выпадения монеты орлом кверху при падении ее с высоты случайным образом?

Начнем подбрасывать монетку и фиксировать результаты каждого броска (см. табл. 21.1).

Таблица 21.1. Результаты испытаний бросания монеты

Количество опытов N                             Значение счетчика выпадения орла Nо               … … … … … … … Значение счетчика выпадения решки Nр               … … … … … … … Частость выпадения орла Pо =Nо/N     0.33 0.25 0.4 0.5 0.57 … … … … … … … Частость выпадения решки Pр =Nр/N     0.66 0.75 0.6 0.5 0.43 … … … … … … …

Будем подсчитывать частость выпадения орла как отношение количества случаев выпадения орла к общему числу наблюдений. Посмотрите в табл. 21.1. случаи для N = 1, N = 2, N = 3 — сначала значения частости нельзя назвать достоверными. Попробуем построить график зависимости P _о от N — и посмотрим, как меняется частость выпадения орла в зависимости от количества проведенных опытов. Разумеется, при различных экспериментах будут получаться разные таблицы и, следовательно, разные графики. На рис. 21.4 показан один из вариантов.

Рис. 21.4. Экспериментальная зависимость частости появления случайного события от количества наблюдений и ее стремление к теоретической вероятности

Сделаем некоторые выводы.

1. Видно, что при малых значениях N, например, N = 1, N = 2, N = 3 ответу вообще доверять нельзя. Например, P _о = 0 при N = 1, то есть вероятность выпадения орла при одном броске равна нулю! Хотя всем хорошо известно, что это не так. То есть пока мы получили очень грубый ответ. Однако, посмотрите на график: в процессе накопления информации ответ медленно, но верно приближается к правильному (он выделен пунктирной линией). К счастью, в данном конкретном случае правильный ответ нам известен: в идеале, вероятность выпадения орла равна 0.5 (в других, более сложных задачах, ответ нам, конечно, будет неизвестен). Допустим, что ответ нам надо знать с точностью ε = 0.1. Проведем две параллельные линии, отстоящие от правильного ответа 0.5 на расстояние 0.1 (см. рис. 21.4). Ширина образовавшегося коридора будет равна 0.2. Как только кривая P _о(N) войдет в этот коридор так, что уже никогда его не покинет, можно остановиться и посмотреть, для какого значения N это произошло. Это и есть экспериментально вычисленное критическое значение необходимого количества опытов N _кр^э для определения ответа с точностью ε = 0.1; ε -окрестность в наших рассуждениях играет роль своеобразной трубки точности. Заметьте, что ответы P _о(91), P _о(92) и так далее уже не меняют сильно своих значений (см. рис. 21.4); по крайней мере, у них не изменяется первая цифра после запятой, которой мы обязаны доверять по условиям задачи.

2. Причиной такого поведения кривой является действие центральной предельной теоремы (см.лекцию 25 и лекцию 34). Пока здесь мы сформулируем ее в самом простом варианте «Сумма случайных величин есть величина неслучайная». Мы использовали среднюю величину P _о, которая несет в себе информацию о сумме опытов, и поэтому постепенно эта величина становится все более достоверной.

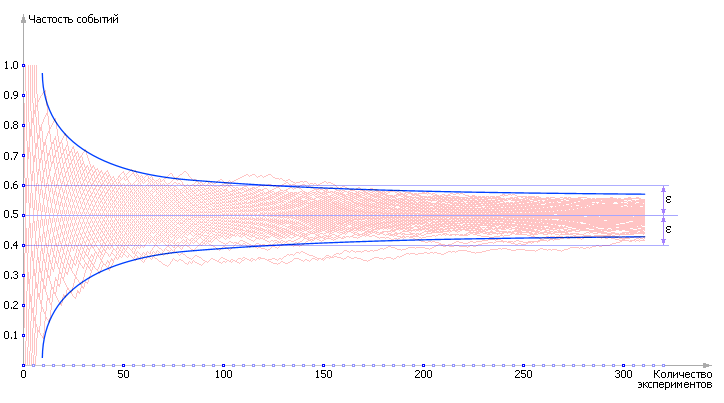
3. Если проделать еще раз этот опыт сначала, то, конечно, его результатом будет другой вид случайной кривой. И ответ будет другим, хотя примерно таким же. Проведем целую серию таких экспериментов (см. рис. 21.5). Такая серия называется ансамблем реализаций. Какому же ответу в итоге следует верить? Ведь они, хоть и являются близкими, все же разнятся. На практике поступают по-разному. Первый вариант — вычислить среднее значение ответов за несколько реализаций (см. табл. 21.2).

Рис. 21.5. Экспериментально снятый ансамбль случайных зависимостей частости появления случайного события от количества наблюдений

Мы поставили несколько экспериментов и определяли каждый раз, сколько необходимо было сделать опытов, то есть N _кр^э. Было проделано 10 экспериментов, результаты которых были сведены в табл. 21.2. По результатам 10-ти экспериментов было вычислено среднее значение N _кр^э.

Таблица 21.2. Экспериментальные данные необходимого количества бросков монеты для достижения точности ε = 0.1 при вычислении вероятности выпадения орла

Опыт Nкрэ                                         Среднее Nкр.э

Таким образом, проведя 10 реализаций разной длины, мы определили, что достаточно в среднем было сделать 1 реализацию длиной в 94 броска монеты.

Еще один важный факт. Внимательно рассмотрите график на рис. 21.5. На нем нарисовано 100 реализаций — 100 красных линий. Отметьте на нем абсциссу N = 94 вертикальной чертой. Есть какой-то процент красных линий, которые не успели пересечь ε -окрестность, то есть (P ^эксп – ε ≤ P ^теор ≤ P ^эксп + ε), и войти в коридор точности до момента N = 94. Обратите внимание, таких линий 5. Это значит, что 95 из 100, то есть 95%, линий достоверно вошли в обозначенный интервал.

Таким образом, проведя 100 реализаций, мы добились примерно 95%-ного доверия к полученной экспериментально величине вероятности выпадения орла, определив ее с точностью 0.1. Для сравнения полученного результата вычислим теоретическое значение N _кр^т теоретически. Однако для этого придется ввести понятие доверительной вероятности Q_F, которая показывает, насколько мы готовы верить ответу. Например, при Q_F = 0.95 мы готовы верить ответу в 95% случаев из 100. Формула теоретического расчета числа экспериментов, которая будет подробно изучаться в лекции 34, имеет вид: N _кр^т = k (Q_F) · p · (1 – p)/ ε ², где k (Q_F) — коэффициент Лапласа, p — вероятность выпадения орла, ε — точность (доверительный интервал). В табл. 21.3 показаны значения теоретической величины количества необходимых опытов при разных Q_F (для точности ε = 0.1 и вероятности p = 0.5).

Таблица 21.3. Теоретический расчет необходимого количества бросков монеты для достижения точности ε = 0.1 при вычислении вероятности выпадения орла

Доверительная вероятность QF Коэффициент Лапласа k(QF) Требуемое число опытов Nкрт = k(QF) · p · (1 – p)/ε2 0.90 2.72   0.95 3.84   0.99 6.66

Как видите, полученная нами оценка длины реализации, равная 94 опытам очень близка к теоретической, равной 96. Некоторое несовпадение объясняется тем, что, видимо, 10 реализаций недостаточно для точного вычисления N _кр^э. Если вы решите, что вам нужен результат, которому следует доверять больше, то измените значение доверительной вероятности. Например, теория говорит нам, что если опытов будет 167, то всего 1-2 линии из ансамбля не войдут в предложенную трубку точности. Но имейте в виду, количество экспериментов с ростом точности и достоверности растет очень быстро.

Второй вариант, используемый на практике — провести одну реализацию и увеличить полученное для нее N _кр^э в 2 раза. Это считают хорошей гарантией точности ответа (см. рис. 21.6).

Рис. 21.6. Иллюстрация экспериментального определения Nкрэ по правилу «умножь на два»

Если присмотреться к ансамблю случайных реализаций, то можно обнаружить, что сходимость частости к значению теоретической вероятности происходит по кривой, соответствующей обратной квадратичной зависимости от числа экспериментов (см. рис. 21.7).

Рис. 21.7. Иллюстрация скорости схождения экспериментально получаемой частости к теоретической вероятности

Это действительно так получается и теоретически. Если изменять задаваемую точность ε и исследовать количество экспериментов, требуемых для обеспечения каждой из них, то получится табл. 21.4.

Таблица 21.4. Теоретическая зависимость количества экспериментов, необходимых для обеспечения заданной точности при QF = 0.95

Точность ε Критическое число экспериментов Nкрт 0.1   0.01   0.001

Построим по табл. 21.4 график зависимости N _кр^т(ε) (см. рис. 21.8).

Рис. 21.8. Зависимость числа экспериментов, требуемых для достижения заданной точности ε при фиксированном QF = 0.95

Итак, рассмотренные графики подтверждают приведенную выше оценку:

Заметим, что оценок точности может быть несколько. Некоторые из них будут еще обсуждаться влекции 34.

Пример 2. Нахождение площади фигуры методом Монте-Карло. Определите методом Монте-Карло площадь пятиугольника с координатами углов (0, 0), (0, 10), (5, 20), (10, 10), (7, 0).

Нарисуем в двухмерных координатах заданный пятиугольник, вписав его в прямоугольник, чья площадь, как нетрудно догадаться, составляет (10 – 0) · (20 – 0) = 200 (см. рис. 21.9).

Рис. 21.9. Иллюстрация к решению задачи о площади фигуры методом Монте-Карло

Используем таблицу случайных чисел для генерации пар чисел R, G, равномерно распределенных в интервале от 0 до 1. Число R будет имитировать координату X (0 ≤ X ≤ 10), следовательно, X = 10 · R. Число G будет имитировать координату Y (0 ≤ Y ≤ 20), следовательно, Y = 20 · G. Сгенерируем по 10 чисел R и G и отобразим 10 точек (X; Y) на рис. 21.9 и в табл. 21.5.

Таблица 21.5. Решение задачи методом Монте-Карло

Номер точки R G X Y Точка (X; Y) попала в прямоугольник? Точка (X; Y) попала в пятиугольник?   0.8109 0.3557 8.109 7.114 Да Да   0.0333 0.5370 0.333 10.740 Да Нет   0.1958 0.2748 1.958 5.496 Да Да   0.6982 0.1652 6.982 3.304 Да Да   0.9499 0.1090 9.499 2.180 Да Нет   0.7644 0.2194 7.644 4.388 Да Да   0.8395 0.4510 8.395 9.020 Да Да   0.0415 0.6855 0.415 13.710 Да Нет   0.5997 0.1140 5.997 2.280 Да Да   0.9595 0.9595 9.595 19.190 Да ⇐ Предыдущая9101112131415161718Следующая ⇒ Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...