Фазовое пространство и аттракторы

 

Теперь от конкретных примеров двумерных отображений перейдем к обсуждению более общих понятий.

Зададимся вопросом: как проследить за эволюцией динамической системы при заданных начальных условиях? Для этого нужно «увидеть», что происходит с задающими динамическую систему переменными x, y,... по мере эволюции во времени. Введем некоторое пространство, по осям координат которого отложим эти переменные. Его принято называть фазовым пространством. Фраза «задано начальное состояние динамической системы» теперь означает, что задана точка в фазовом пространстве. «Включим» время. Если система определена дискретным отображением, например, отображением Эно или отображением прыгающего шарика, то изображающая точка при каждой итерации

будет совершать «прыжки» в фазовом пространстве.

Динамическая система полностью задает закон эволюции во времени, однако, чтобы получить полную информацию о характере такой эволюции, надо провести исследование для различных начальных условий. Современные компьютеры делают эту задачу не умозрительной, а вполне реальной и позволяют получать наглядные геометрические образы такого процесса.

Итак, рассмотрим множество начальных состояний системы. В фазовом пространстве в этом случае будем иметь уже не одну изображающую точку, а некоторый набор, или облако точек. При «включении» времени они все начнут совершать «прыжки». При компьютерном моделировании разумно создать мгновенные «снимки» облака через определенные промежутки времени (число итераций). Тогда можно следить за эволюцией облака на экране дисплея.

Перейдем к компьютерному моделированию. В качестве исследуемой системы выберем отображение Энона (65). На рис. 39 показаны мгновенные «снимки» облака изображающих точек на фазовой плоскости для отображения Энона, сделанные через одну итерацию.

Наиболее существенный результат, вытекающий из компьютерного моделирования, состоит в том, что облако изображающих точек «конденсируется» на некоторые предельные объекты, размерность которых меньше, чем размерность фазового пространства. Их называют аттракторами (от английского to attract – притягивать). Полезно также привести сравнительно строгое определение: аттрактором называется множество в фазовом пространстве, обладающее следующими свойствами:

1. Его размерность меньше, чем размерность фазового пространства (т.е. для двумерных отображений, например, аттрактором не может быть некоторая область плоскости).

2. Это множество инвариантно относительно действия отображения (т.е. если точка принадлежит аттрактору, то после действия отображения она останется на аттракторе).

3. Существует некоторое множество в фазовом пространстве, обязательно включающее аттрактор и его некоторую малую окрестность, все точки которого после некоторого (быть может, очень большого) количества итераций отображения окажутся на аттракторе. Это множество называется бассейном притяжения (или просто бассейном) аттрактора.

 

 

Рис. 39. Конденсация облака изображающих точек в фазовом пространстве для

отображения Энона (65). Значения параметров λ = 1,4, b = 0,3.

 

Поскольку в соответствии с первым свойством размерность аттрактора меньше, чем размерность фазового пространства (это хорошо заметно на рис. 39), то занимаемый выбранным облаком точек объем в фазовом пространстве (обычно его называют фазовым объемом) должен уменьшаться при итерациях отображения. Динамические системы, которые обладают таким свойством (а, следовательно, и аттракторами) называются диссипативными, а динамические системы, фазовый объем в которых не изменяется со временем – консервативными. Поведение диссипативных и консервативных динамических систем весьма различно, и в настоящей книге мы будем рассматривать только диссипативные системы.

Важной характеристикой отображения, позволяющей судить о наличии сжатия фазового пространства, является его якобиан.

Пусть имеется двумерное отображение общего вида

 

 

Неподвижная точка этого отображения удовлетворяет условию

 

 

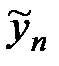Динамика малых возмущений этой неподвижной точки и в линейном приближении будет описываться соотношением:

 

 

где матрица возмущений M составлена из соответствующих производных

 

 

Определитель J = этой матрицы, вычисленный в неподвижной точке, называется якобианом и определяет, как известно из математического анализа, эволюцию малого элемента площади при действии отображения. При J < 1 этот элемент сжимается, так что отображение будет диссипативным. Если J = 1, то отображение оказывается консервативным, и фазовый объем по мере эволюции не меняется.

Найдем для примера якобиан отображения Энона. Вычисляя соответствующие частные производные, находим:

 

 

В этом случае якобиан J = b. Таким образом, параметр b управляет степенью сжатия фазового элемента. При b = 0 оно «бесконечно сильное», так что отображение Эно редуцирует к одномерному логистическому отображению. При b = 1 реализуется противоположный предельный случай – консервативная система.

Отображение Энона представляет пример систем с постоянным якобианом. В более общем случае якобиан системы может зависеть от значений динамических переменных, так что в отдельных областях фазового пространства наблюдается сжатие, а в других – растяжения фазового элемента. В этом случае могут возникать новые эффекты, которые будут обсуждаться ниже.

Итак, диссипативные динамические системы обладают аттракторами. Это свойство является очень важным и существенно упрощает процесс исследования таких систем. Ведь вследствие притяжения к аттрактору траектории, стартовавшие из различных точек, с течение времени приходят к одной и той же, то есть со временем система «забывает» начальные условия и ее поведение определяется только значениями параметров. Следовательно, для изучения поведения диссипативной динамической системы достаточно исследовать ее аттракторы. Это, в частности, существенно упрощает компьютерное моделирование: не надо следить за всеми изображающими точками14. Достаточно выбрать одну из них, выполнить определенное (не очень маленькое) число итераций, чтобы эта точка «вышла» на аттрактор, а затем вывести ее движение на экран компьютера. Тогда мы и получим портрет аттрактора.

Аттракторы динамических систем могут быть как очень простыми (неподвижная точка, цикл определенного периода), так и более сложными. Пример такого сложного аттрактора дает рис. 39, демонстрирующий, что изображающие точки притягиваются к некоторой сложной слоистой структуре. Если просмотреть с помощью компьютера как «микроскопа» отдельные фрагменты такого аттрактора, то обнаруживается, что он весь состоит из отдельных «нитей» и областей пустого пространства, причем каждая нить в свою очередь имеет аналогичную тонкую структуру (см. рис. 40). Как говорят, аттрактор в этом случае обладает фрактальными свойствами. Подобные аттракторы были обнаружены в семидесятые годы нашего века и получили название странных. Обыкновенно (но не всегда) им соответствует режим динамического хаоса.

 

 

Рис.40. Фрактальная структура аттрактора отображения Энона (65). Значения параметров λ = 1,4 и b = 0,3.

 

 

 

% Henon_map_ (a,b)

a=1.4; b=0.3;

N=6000;

x=zeros(1,N);

y=zeros(1,N);

x(1)=0.1;

y(1)=0;

for i=1:N

x(i+1)=1+y(i)-a*(x(i))^2;

y(i+1)=b*x(i);

end

axis([-1,2,-1,1])

figure

plot(x,y,'.')

fsize=15;

set (gca,'xtick',[-1:1:1],'FontSize',fsize)

set (gca,'ytick',[-1:1:2],'FontSize',fsize)

xlabel('\itx','FontSize',fsize)

ylabel('\ity','FontSize',fsize)

 

Система Лоренца

 

АВТОКОЛЕБАНИЯ - незатухающие колебания в диссипативной нелинейной системе, поддерживаемые за счёт энергии внеш. источника, параметры к-рых (амплитуда, частота, спектр колебаний) определяются свойствами самой системы и не зависят от конечного изменения нач. условий. Термин "А." введён А. А. Андроновым в 1928.

А. принципиально отличаются от др. колебат. процессов в диссипативных системах тем, что для их поддержания не требуется колебат. воздействий извне. Примеры А.: колебания скрипичной струны при движении смычка, тока в радиотехн. генераторе, воздуха в органной трубе, маятника в часах. Возникают А. в результате развития колебат. неустойчивостей с их последующей стабилизацией из-за прекращения поступления энергии от источника или прогрессирующего возрастания потерь (диссипации). Режим стационарных А. определяется из условия энергетич. баланса - в ср. за период диссипативные траты энергии Q (I) (I - интенсивность А.) должны точно компенсироваться поступлением энергии W(I)от источника: .

 

Конкуренция мод - подавление одних мод другими в автоколебат. системах - связана с тем, что конкурирующие моды черпают энергию на покрытие дисси-пативных расходов из общего источника. В результате одни моды создают дополнит. нелинейное затухание для других. Благодаря эффектам конкуренции и взаимной синхронизации колебаний в автоколебат. системах с большим числом степеней свободы (или даже бесконечным числом - в случае распределённых систем) возможно установление из нач. шума (нарастающих в результате развития линейных неустойчивостей флуктуации на разл. частотах) режима регулярных периодич. А. Эффекты конкуренции и синхронизации оказываются принципиальными и для появления высокоорганизованных структур в нелинейных не равновесных средах.

В распределённых системах характер А. существенно зависит, помимо вида нелинейности, ещё и от особенностей дисперсии среды и граничных условий, в частности наличия резонатора. В нек-рых случаях спектр возбуждения мод и особенности их нелинейного взаимодействия таковы, что при анализе А. в распределённой системе с бесконечным числом степеней свободы возможно ограничиться т.н. одномодовым описанием.

Рис. 7. Кольцевая труба, заполненная жидкостью,- конвективная петля; g- ускорение силы тяжести, Т_Н – темп-pa в точке М, T_В - темп-pa в точке Р.

 

Для примера рассмотрим А. в кольцевом резонаторе - расположенной в вертик. плоскости замкнутой трубе, заполненной вязкой жидкостью (рис. 7). При подогреве кольца снизу в системе устанавливается режим конвекции: более лёгкая, нагретая в основании кольца часть жидкости всплывает, заставляя охлаждённую жидкость опускаться вниз. Т. о., начиная с нек-рой разности темп-р Т_В - Т_Н= устанавливается режим стационарного вращения жидкости по или против часовой стрелки. При этом вся жидкость вращается как целое - реализуется лишь одно наиб. крупномасштабное движение. Дальнейшее увеличение приводит к возникновению А., проявляющихся в том, что жидкое кольцо внутри трубы время от времени будет менять направление своего движения. Физически это можно пояснить так: пусть в данный момент жидкость движется по часовой стрелке, при достаточно большом архимедова сила велика и водяное кольцо ускоряется настолько, что остывший вверху жидкий объём, пройдя горячее основание и не успев нагреться, уже не достигает верх. части кольца и приостанавливается (архимедова сила недостаточна, чтобы преодолеть силу вязкости и гравитации). При этом опускающаяся (правая) часть жидкости теплее и, следовательно, легче поднимающейся.

В результате торможения жидкого кольца жидкость в его основании нагревается и всплывает, но уже в противоположном направлении - давление справа меньше, чем слева. Т. о., жидкое кольцо меняет направление своего вращения и начинает закручиваться против часовой стрелки. Затем всё повторяется в обратном порядке. Такие вызываемые тепловой конвекцией А. могут быть как периодическими, так и стохастическими. Поскольку никакие другие масштабы движения, кроме основного, в А. рассматриваемого вида не участвуют, матем. модель для описания этих А. может быть получена из исходных ур-ний гидродинамики в предположении, что зависимость полей скорости и темп-ры от пространственных координат не меняется во времени и пропорциональна , где 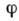- угл. координата элементарного объёма жидкости. В результате для безразмерных скорости x(t)движения жидкого кольца, темп-ры y(t)жидкости в точке N и темп-ры z(t)в точке М можно получить систему ур-ний в обыкновенных производных:

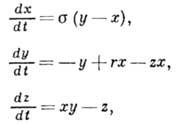(3),

где , . Это - известная система Лоренца, к-рая является одной из осн. моделей теории стохастич. А. В зависимости от параметров и в фазовом пространстве системы (3) могут существовать как устойчивый предельный цикл, так и странный аттрактор.

В общем случае А. в резонаторах, к-рые описываются ур-ниями в частных производных с соответствующими граничными условиями, невозможно представить с помощью конечномерной динамич. системы. Однако, как правило, благодаря разного рода физ. обстоятельствам, напр. наличию диссипации, прогрессирующей с ростом частоты или уменьшением пространственного масштаба пульсаций, такое конечномерное описание оказывается справедливым.

В неравновесных диссипативных средах, помимо А., о к-рых речь шла выше, возможны ещё т. н. авто-волны и автоструктуры - не связанные с граничными условиями пространственно-временные образования, параметры к-рых определяются лишь свойствами нелинейной неравновесной среды, напр. уединённые фронты горения и волны популяций, импульсы в нервных волокнах, цилиндрические и спиральные волны в сердечной ткани и др. Стохастич. А. в нелинейных неравновесных средах - это турбулентность.

 

Лоренца система

www.femto.com.ua

 

Рис. 1. Иллюстрация последовательных бифуркаций в системе Лоренца при увеличении параметра r: а) ; б) ; в) г) д) е)

 

Л. с. – один из примеров ДС, имеющей простой физ. смысл; она демонстрирует стохастич. поведение системы. В фазовом пространстве этой системы в области параметров, указанных на рис. 1, существует странный аттрактор, движение изображающей точки на к-ром соответствует "случайному" – турбулентному течению жидкости при тепловой конвекции.

Рис. 2. Конвективная петля - физическая модель, для которой выводятся уравнения Лоренца.

Л. с. (при b = l) описывает, в частности, движение жидкости в конвективной петле, расположенной в вертикальной плоскости в однородном поле тяжести тороидальной полости, заполненной жидкостью (рис. 2). На стенках полости поддерживается не зависящая от времени (но зависящая от угла ) темп-pa Т( ); ниж. часть петли теплее верхней. Ур-ния движения жидкости в конвективной петле сводятся к Л. с., где x(t] - скорость движения жидкости, у (t) - темп-pa в точке N, a z(t) - темп-pa в точке М при больших t. С ростом г характер движения жидкости меняется: сначала (при г<1) жидкость неподвижна, далее (при ) устанавливается циркуляция с пост. скоростью (либо по часовой стрелке, либо против); при ещё больших r всё течение становится чувствительным к малым изменениям нач. условий, скорость циркуляции жидкости меняется уже нерегулярно: жидкость вращается иногда по часовой стрелке, иногда - против.

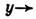
При обычно используемых значениях Pr =10, b= 8/3 Л. с. обладает след. свойствами: ур-ния Л. с. инварианты относительно преобразования , фазовый объём сокращается с пост. скоростью

за единицу времени объём сокращается в 10⁶ раз. С ростом г в Л. с. происходят след. осн. бифуркации. 1) При единственным состоянием равновесия является устойчивый узел в начале координат О (О, О, 0). 2) При , где r ₁=13,92, Л. с. кроме упомянутого тривиального (О)имеет ещё два состояния равновесия , . Состояние равновесия О является седлом, имеющим двумерное устойчивое многообразие и одномерное неустойчивое, состоящее из О и двух сепаратрис и , стремящихся к и (рис. 1, а). 3) При r = r ₁ каждая из сепаратрис становится двоякоасимпто-тической к седлу О (рис. 1, б). При переходе r через r ₁ из замкнутых петель сепаратрис рождаются неустойчивые (седловые) периодич. движения - предельные циклы L ₁ и L ₂. Вместе с этими неустойчивыми циклами рождается и очень сложно организованное предельное множество; оно, однако, не является притягивающим (аттрактором), и при (рис. 1, в), где r ₂=24,06, все траектории по-прежнему стремятся к . Эта ситуация отличается от предшествующей тем, что теперь сепаратрисы _ и идут к "не своим" состояниям равновесия и соответственно. 4) При , гдо 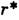= 24,74, в Л. с. наряду с устойчивыми состояниями равновесия существует ещё притягивающее множество, характеризующееся сложным поведением траекторий,- аттрактер Лоренца (рис. 1, д и рис. 3). 5) При седловые циклы L ₁ и L ₂ стягиваются к состояниям равновесия и 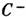, к-рые при теряют устойчивость, и при единственным притягивающим множеством Л. с. является аттрактор Лоренца. Т. о., если стремить к со стороны меньших значений, то стохастичность в Л. с. возникает сразу, скачком, т. е. имеет место жёсткое возникновение стохастичности.

Рис. 3. Траектория, воспроизводящая аттрактор Лоренца (выходит из начала координат); горизонтальная плоскость соответствует r = = 27, r =28.

К Л. с. сводятся не только ур-ния, описывающие конвективные движения жидкости, но и др. физ. модели (трёхуровневый лазер, дисковое динамо и т. д.).

Литература: Lorenz E., Deterministic nonperiodic flow, "J. Atmos. Sci.", 1963, v. 20, p. 130; в рус. пер., в кн.: Странные аттракторы, М., 1981, с. 88; Гапонов-Грехов А.В., Рабинович М.И., Хаотическая динамика простых систем, "Природа", 1981, № 2, с. 54; Афраймович В.С., Быков В.В., Шильников Л.П., О притягивающих негрубых предельных множествах типа аттрактора Лоренца, "Тр. Московского матем. общества", 1982, т. 44, с. 150; Рабинович М.И., Трубецков Д.И., Введение в теорию колебаний и волн, М., 1984.

В. Г. Шехов.

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Система Лоренца

 

Система трёх нелинейных ДУ первого порядка:

 

 

решения которой в широкой области параметров являются нерегулярными функциями времени и по многим своим характеристикам неотличимы от случайных. Система Лоренца была получена Э. Лоренцем (Е. Lorenz) из уравнений гидродинамики как модель для описания тепловой конвекции в горизонтальном слое жидкости, подогреваемой снизу.

 

•β - отношение вертикальных и горизонтальных размеров конвективной ячейки

•σ- безразмерное число Прандтля

 

• r = R / R_кр – приведенное число Релея.

 

Число Релея

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: