 |
Эффективная ставка операции.
|
|
|
|
Задача 31.
Сравнить эффективность трех сделок:
1. В начале первого года банк дает фирме кредит в размере 3 млн руб. В конце второго года фирма возвращает 4 млн руб.
2. Банк дает фирме кредит в два этапа: в начале первого года – 2 млн руб., в начале второго года – 1 млн руб. В конце второго года фирма возвращает 4 млн.руб.
3. Банк дает фирме кредит в два этапа: в начале первого года – 1 млн руб., в начале второго года – 2 млн руб. В конце второго года фирма возвращает 4 млн руб.
Задача 32.
Сравнить эффективность четырех сделок:
1. В начале первого года банк дает фирме кредит в размере 5 млн руб. В начале второго года фирма возвращает 2 млн руб. В конце второго года фирма возвращает 4 млн руб.
2. Банк дает фирме кредит в два этапа: в начале первого года – 3 млн руб., в начале второго года – 2 млн руб. В конце второго года фирма возвращает 6 млн руб.
3. Банк дает фирме кредит в два этапа: в начале первого года – 2 млн руб., в начале второго года – 3 млн руб. В конце второго года фирма возвращает 6 млн руб.
4. В начале первого года банк дает фирме кредит в размере 5 млн руб.
В конце второго года фирма возвращает 6 млн руб.
Задача 33.
Кредит 100 тыс. руб. выдан банком на 10 месяцев под 12 % годовых. Договор предусматривает дополнительные ежемесячные выплаты на обслуживание кредита в размере 1 % от суммы кредита и комиссионный сбор в момент заключения сделки в размере 2 % от суммы кредита. Найти размер месячного платежа и эффективную ставку сделки. Какая схема погашения кредита выгоднее: аннуитетная (равными платежами) или дифференцированная? Может быть, лучше погашать кредит по дифференцированной схеме, тогда и эффективная ставка будет меньше?
Для определения эффективной ставки использовать финансовые функции Excel.
|
|
|
Занятие № 3. Тема «финансовые вычисления по ценным бумагам»
Оценка облигаций с нулевым купоном
Задача 34.
Оценить текущую стоимость облигации с нулевым купоном номинальной стоимостью 1000 руб. и сроком погашения через 3 года. Ставка дисконта r=20 %.
Оценка облигации с фиксированной ставкой
Задача 35.
Оценить текущую стоимость облигации (PV) по номинальной стоимости
1 млн руб. с купонной ставкой rk=20 %, дисконтом r=12 %. Срок погашения 5 лет.
Оценка бессрочных облигаций с постоянным доходом
Задача 36.
Оценить текущую стоимость бессрочной облигации, если по ней ежегодно выплачивается доход 1 тыс. руб. Ставка дисконта r=10 %.
Оценка обыкновенных акций
Задача 37.
Оценить текущую стоимость акции, если каждый год дивиденд равен 100 тыс. руб. Ставка дисконта r=5 %.
Акции с равномерно возрастающими дивидендами
Задача 38.
Компания начальный дивиденд D=10 тыс. руб. ежегодно наращивает с темпом роста q=3 %. Найти текущую стоимость акций компании при ставке дисконта r=8 %.
Занятие № 4. Тема «оценка эффективности инвестиционного проекта»
Задача 39
Оценить эффективность инвестиций, заданных двусторонним потоком платежей:
01.01.10 12 млн руб.
01.01.11 10 млн руб.
01.01.12 15 млн руб.
01.01.13 9 млн руб.
01.01.14 9 млн руб.
01.01.15 9 млн руб.
01.01.16 9 млн руб.
01.01.17 9 млн руб.
01.01.18 9 млн руб.
01.01.19 9 млн руб.
Для этого вычислить:
1- Чистое современное значение потока платежей NVP при процентной ставке r = 10 %.
2- Эффективную ставку (внутреннюю эффективность) потока платежей IRR.
3- Время окупаемости инвестиционного проекта при процентной ставке
r = 8%; r = 10 %; r = 12 %.
4- Норму (индекс) рентабельности инвестиционного проекта.
Воспользоваться функциями Excel.
Занятие № 5. Тема «финансовый риск»
Неравенство Чебышева
Теорема Чебышева
Вероятность того, что случайная величина R отклонится от своего математического ожидания m больше, чем заданное значение d, не превосходит ее дисперсии s2, деленной на d2, т. е.:
|
|
|
, (5.4)
где Р(*) обозначает вероятность события *.
Воспользоваться теоремой Чебышева для решения следующей задачи.
Задача 40.
Господин А делает заем под процент r и под залог недвижимости. На полученные взаймы деньги господин А покупает акции. Пусть эффективность R покупаемых господином А акций характеризуется математическим ожиданием дохода m и дисперсией s2, оценивающей рискованность финансовой операции. Найти соотношение между r, m, s, при которой вероятность того, что господин А не сможет вернуть долг и лишится недвижимости меньше или равна 0,04.
Хеджирование
Для иллюстрации хеджирования рассмотрим следующий модельный пример.
Инвестор-кредитор А собирается вложить сумму С в дело под r процентов. Ожидаемый доход равен R=Cr. Однако операция инвестору представляется рискованной, и он решает приобрести страховой полис, гарантирующий выплату определенной суммы в случае провала сделки.
Для этого сумму С инвестор разделяет на две части: Cx он вкладывает в сделку и, C(1-x) он тратит на страховку, где х, 1-х – доля суммы, потраченная на финансовую сделку и страховой полис соответственно. Возможны два варианта развития событий.
Вариант 1.
Сделка оказалась удачной. В результате получен доход:
.
Вариант 2.
Сделка не удалась. Инвестор получает страховую выплату в размере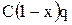 
, где q – отношение страхового возмещения к цене полиса. Тогда полученный доход равен:
.
Очевидно, логично выбрать х так, чтобы доход в обоих случаях был одинаков R1=R2. Решив линейное уравнение, получим:
.
При этом доход будет равен:
.
Таким образом, данная схема хеджирования исключает неопределенность, при этом эффективность сделки снижается с r до 
.
Задача 41.
Рассмотреть численный пример хеджирования. Пусть r=0,1, а q=40. Найти долю средств, отпускаемых на сделку и долю средств на страховку. Определить эффективность хеджирования.
|
|
|
