 |
Относительная погрешность, граница относительной погрешности являются безразмерными величинами.
|
|
|
|
Определение: Границей относительной погрешности приближения называется положительное число Е, которое больше или равно самой относительной погрешности.
; 
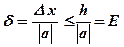Пример:
1. Сравнить качество двух измерений:
а) длина предмета а1= 1,2 м, D х1= 0,005 м;
б) расстояние а2 = 6,76 км, D х2 = 10 м.
Решение:
При первом измерении допущена погрешность D х1 = 0,005 м = 5 мм на 1,2 м =
= 1200 мм. Определим относительную погрешность первого измерения, то есть какую часть (сколько %) составляет абсолютная погрешность Dх1 от приближенного значения а1 .
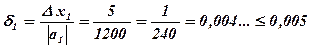;Е1 = 0,005 = 0,5 %.
Определим относительную погрешность второго измерения, то есть какую часть (сколько %) составляет абсолютная погрешность Dх2 = 10 м от приближенного значения а2 = 6,76 км = 6760 м.
;Е2 = 0,002 = 0,2 %.
Е2 £ Е1 , следовательно, качество второго измерения лучше.
Ответ: Качество второго измерения лучше.
2. Термометр дает отклонение не более 0,5° С. Им измерили температуру воздуха и получили 17° С. С какой относительной точностью выполнено измерение?
а = 17° С Под относительной точностью понимается граница
h = 0,5° С относительной погрешности данного измерения.
Е =? 
;Е = 3 %.
Ответ: Е = 3 %.
Упражнения:
1. Сравнить качество двух измерений:
а) масса железнодорожного вагона т1 = 63 ± 0,5(т);
б) масса дозы лекарства т2 = 0,15 ± 0,005(г).
2. Определить границу относительной погрешности следующих чисел:
а) а = 142,5; D х = 0,05; г) а = 2,372; D х = 0,004;
б) а = 6,93; D х = 0,02; д) а = 12,79; D х = 2.
3. Найти границу абсолютной погрешности числа а = 1348, если Е = 0,04 %.
4. Известно, что х» а с точностью до Е %. Найти границу абсолютной погрешности приближения, если:
а) а = 2,75; Е = 20 %; в) а = 237; Е = 1 %;
б) а = 1,3; Е = 10 %; г) а = 1,49; Е = 0,1 %.
3. Верные и сомнительные цифры приближенного значения числа.
|
|
|
Значащие цифры приближенного значения числа
При вычислениях часто трудно указать наряду с приближенными значениями их погрешности. А в различных справочниках указывать погрешности приближенных данных неудобно, неэкономично. Поэтому при записи приближенных значений чисел требуют, чтобы по этой записи можно было определить границу абсолютной погрешности приближения. Для этого вводится понятие верной и сомнительной цифр приближенного значения числа.
Определение: Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не превосходит (£) единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной.
Пример: Определить верные и сомнительные цифры в приближенном значении числа:
1. х = 35,4 ± 0,08
В записи приближенного значения числа цифра 4 находится в разряде десятых (0,1); граница абсолютной погрешности h = 0,08 не превосходит 0,1, следовательно, 4 – верная цифра. Очевидно, что все остальные цифры – верные.
Вывод: Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.
2. х = 9,846 ± 0,04
Цифра 6 находится в разряде 0,001; h = 0,04 £ 0,001, 6 – сомнительная цифра;
Цифра 4 в 0,01; h = 0,04 £ 0,01; 4 – сомнительная цифра;
Цифра 8 в 0,1; h = 0,04 £ 0,1; 8 – верная цифра;
Следовательно, 9 – верная цифра.
3. х = 945,673 ± 0,03
Цифра 3 в 0,001; h = 0,03 £ 0,001; 3 – сомнительная цифра;
Цифра 7 в 0,01; h = 0,03 £ 0,01; 7 – сомнительная цифра;
Цифра 6 в 0,1; h = 0,03 £ 0,1; 6 – верная цифра;
Следовательно, 5, 4, 9 – верные цифры.
При записи приближенных чисел принято соблюдать следующие правила.
Правила записи приближенных чисел:
- В записи приближенного числа сохраняют только верные цифры, сомнительные цифры округляют.
- Если в десятичной дроби последние верные цифры оказались нулями, то их надо сохранить в записи.
- Если целое число содержит в конце нули, оказавшиеся сомнительными цифрами, то они должны быть заменены на сомножитель 10 п, где п – число нулей, которые надо заменить.
Пример: Записать правильно приближенное значение числа:
|
|
|
1. х = 950,031 ± 0,04
Цифра 1 в 0,001; h = 0,04 £ 0,001, 1 – сомнительная цифра;
Цифра 3 в 0,01; h = 0,04 £ 0,01, 3 – сомнительная цифра;
Цифра 0 в 0,1; h = 0,04 £ 0,1, 0 – верная цифра;
|
|
|
