Однофакторный корреляционно-регрессионный анализ

 

Одна из задач экономической науки заключается во всестороннем изучении связей и зависимостей между явлениями и процессами. Различают два вида связей между явлениями: функциональную и корреляционную.

Функциональная связь выражается в том, что определенному значению одной переменной величины (факторный признак) соответствует строго определенное значение другой переменной величины (результативный признак). В этом случае значение результативного признака можно рассчитать по аналитической формуле, которая отражает связь между данными признаками.

Связь между социально-экономическими явлениями проявляется, главным образом, в форме корреляционной связи. При корреляционной связи на величину результативного признака, кроме факторного признака, оказывает влияние множество других причин, некоторые из которых могут быть нам неизвестны. Каждому значению факторного признака здесь будет соответствовать не одно определенное значение результативного признака, а целая совокупность их. Корреляционная связь проявляется в виде общей тенденции к возрастанию или убыванию результативного признака при возрастании или убывании факторного признака. Например, стаж рабочего и его производительность труда. Между ними существует корреляционная зависимость. Стаж работы влияет на производительность труда, но не определяет ее, так как помимо стажа на производительность труда влияют и другие факторы, такие, как квалификация, возраст, личные качества рабочего и т.д. Если бы стаж был единственным фактором, влияющим на производительность труда, между ними была бы не корреляционная, а функциональная зависимость.

Важная особенность корреляционных связей состоит в том, что они обнаруживаются не в единичных случаях, а в массе и требуют для своего исследования массовых наблюдений. В этом отношении проявление корреляционных зависимостей связано с действием закона больших чисел: лишь в достаточно большом числе фактов индивидуальные особенности и второстепенные факторы сгладятся, и зависимость, если она имеет существенную силу, проявляется достаточно отчетливо. Функциональная связь и полное отсутствие связи являются предельными случаями корреляционной связи.

Проблема измерения связи имеет две стороны: определение формы связи и установление тесноты связи. Определением формы связи занимается регрессионный анализ, а установлением тесноты связи — корреляционный анализ.

При определении формы корреляционной связи различают связь прямую и обратную. Под прямой понимают такую связь, когда с увеличением факторного признака результативный признак обнаруживает тенденцию к увеличению, а с уменьшением факторного признака – к уменьшению. При обратной же связи с увеличением (уменьшением) факторного признака результативный признак обнаруживает тенденцию к снижению (увеличению).

Задача регрессионного анализа состоит в том, чтобы подыскать такую форму функциональной связи, которая в наилучшей степени отвечала бы сущности обнаруженной корреляционной зависимости. Определение формы связи заключается в выявлении аналитической функции, с помощью которой выражается эта связь между признаками. Найденную функцию называют уравнением регрессии. В общем виде при парной зависимости уравнение регрессии может быть представлено следующим образом:

, (1)

где y_x — расчетное (теоретическое) значение результативного признака;

x — факторный признак.

 

 

Различают линейные и нелинейные уравнения регрессии. Линейное уравнение регрессии имеет следующий вид:

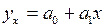, (2)

где a₀ — свободный член;

a₁ — коэффициент регрессии.

Наиболее часто в статистическом анализе взаимосвязей применяются следующие нелинейные зависимости:

уравнение гиперболы:		(3)
уравнение степенной функции:		(4)
уравнение показательной функции:		(5)
уравнение логарифмической связи:		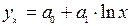(6)
уравнение полинома второго порядка:		(7)

 

В этих формулах a₀, a₁ и a₂ — постоянные величины, называемые параметрами уравнений регрессии.

Параметры уравнений регрессии определяются по методу наименьших квадратов. Сущность этого метода заключается в том, что отыскиваются такие значения коэффициентов уравнения регрессии, при которых сумма квадратов отклонений фактических значений результативного признака y от вычисленных по уравнению y_x будет наименьшей из всех возможных.

Требуется подобрать параметры функции

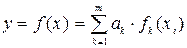
таким образом, чтобы сумма квадратов отклонений искомой аналитической функции от экспериментальной была наименьшей:

.

Для отыскания минимума этой разности необходимо найти частные производные функции Z по всем неизвестным параметрам и приравнять их к нулю. Рассмотрим в качестве примера применение метода наименьших квадратов, когда для аппроксимации экспериментальной зависимости выбрано уравнение прямой: .

Для определения неизвестных параметров a₀ и a₁ методом наименьших квадратов составим сумму квадратов отклонений искомой аналитической функции от наблюдаемых значений в точках (x₁y₁, x₂y₂,..., x_ny_n):

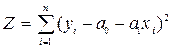. (8)

Продифференцируем функцию Z по параметрам a₀ и a₁. Приравнивая производную нулю, получим следующую систему уравнений:

- ;

-

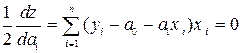
или

;

. (9)

Для нахождения параметров a₀ и a₁ в уравнении линейной регрессии (2) необходимо решить систему нормальных уравнений (9).

Аналогичным образом определяются параметры уравнений регрессии при использовании нелинейных зависимостей.

Если относительно формы связи могут быть выдвинуты различные гипотезы и качественный анализ не позволяет отдать предпочтение ни одной из них, строятся уравнения регрессии с различными формами связи и сравниваются коэффициенты детерминации (расчет этого коэффициента см. ниже), вычисленные для уравнений регрессии разного вида. Если для некоторой функции коэффициент детерминации окажется выше, чем для других, это будет свидетельствовать о том, что соответствующее уравнение регрессии лучше согласуется с эмпирическими данными и его целесообразно использовать для моделирования корреляционной связи.

Задача корреляционного анализа состоит в том, чтобы определить с помощью специальных показателей, в какой мере корреляционная связь приближается по своей силе к функциональной.

При линейной зависимости между признаками для определения тесноты корреляционной связи применяется коэффициент корреляции, который вычисляется по формуле:

R= . (10)

Коэффициент корреляции принимает значения от -1 до +1. Положительные его значения свидетельствуют о наличии прямой связи, отрицательные – обратной. Знак при R совпадает со знаком коэффициента регрессии a₁.

Абсолютная величина R, лежащая между 0 и 1, служит мерой тесноты связи. В зависимости от величины R можно сделать следующие заключения о степени тесноты связи:

0<= R<0,2 – практически нет связи;

0,2<= R< 0,5 – слабая (не тесная) связь;

0,5<= R<0,75 – средняя связь;

0,75<= R<0,95 – сильная (тесная) связь;

0,95<= R<1,00 – практически функциональная связь.

Если R по абсолютной величине равен 1, это свидетельствует о том, что связь между признаками является функциональной, т.е. факторный признак полностью определяет результативный.

При линейной и нелинейной зависимости между признаками для определения тесноты связи используется корреляционное отношение, которое рассчитывается по формуле:

, (11)

где s _ф² – дисперсия, измеряющая вариацию результативного признака за счет действия факторного признака (факторная дисперсия);

s _y² – дисперсия, измеряющая общую вариацию результативного признака за счет действия всех факторов, от которых он зависит (общая дисперсия).

Факторная и общая дисперсия определяются по формулам:

, (12)

, (13)

где – теоретические (расчетные) значения результативного признака, найденные по уравнению регрессии;

– среднее значение результативного признака;

– фактическое значение результативного признака.

Корреляционное отношение изменяется от 0 до 1. Чем ближе корреляционное отношение к 1, тем связь между признаками теснее. В случае линейной зависимости между признаками корреляционное отношение численно равно коэффициенту корреляции. Если корреляционное отношение применяется при изучении тесноты нелинейной связи между признаками, его называют индексом корреляции. Для упрощения расчетов индекс корреляции рассчитывается по следующей формуле:

, (14)

где s₀² – дисперсия, измеряющая вариацию результативного признака за счет действия остальных факторов, кроме x (остаточная дисперсия).

Остаточная дисперсия рассчитывается по формуле:

. (15)

Величина h² (при линейной связи R²) называется коэффициентом детерминаци и D. Коэффициент детерминации показывает, какая доля вариации результативного признака обусловлена вариацией факторного признака, входящего в соответствующее уравнение регрессии. Величина I - h² (или I - R²) является коэффициентом остаточной детерминации и характеризует долю вариации (можно в процентах) за счет неучтенных факторов.

Уравнение регрессии, исчисленное для ограниченной по объему совокупности, может быть искажено действием случайных факторов. Поэтому необходимо проверить, насколько это уравнение характерно для того комплекса условий, в которых находится исследуемая совокупность, не является ли оно результатом стечения случайных обстоятельств. Проверка значимости (существенности) уравнения регрессии проводится с помощью F-критерия (критерия Фишера), исчисляемого по формуле:

, (16)

где m – число параметров в уравнении регрессии.

Полученное значение F-критерия сравнивается с табличным (критическим) для выбранного уровня значимости и чисел степеней свободы k₁ = m - 1 и k₂ = n - m. Если фактическое значение F-критерия превышает его табличное значение, то уравнение регрессии признается статистически значимым.

Таким образом, однофакторный корреляционно-регрессионный анализ заключается в построении и оценке статистической модели в виде уравнения регрессии, приближенно выражающего зависимость результативного признака от одного факторного признака.

Результаты корреляционно-регрессионного анализа в значительной мере зависят от качества исходной информации, которая должна быть достаточно большой по объему, чтобы в силу действия закона больших чисел определяемые в процессе корреляционно-регрессионного анализа статистические характеристики были достаточно типичными и надежными.

Важным условием правильного применения корреляционно-регрессионного анализа является требование качественной и количественной однородности исходных данных. Качественная однородность предполагает близость условий формирования результативных и факторных признаков. Так, например, при корреляционно-регрессионном анализе зависимостей тех или иных технико-экономических показателей работы предприятий от определенных факторов необходима однородность предприятий по виду выпускаемой продукции, характеру технологического процесса и типу используемого оборудования. Количественная однородность заключается в отсутствии единиц наблюдения, которые по своим числовым характеристикам существенно отличаются от основной массы данных.

Поделиться:

Воспользуйтесь поиском по сайту: