 |
Постановка задачи векторной оптимизации. Принципы оптимальности
|
|
|
|
Н.Б. Баева, Ю.В. Бондаренко, Т.В. Азарнова, И.Л. Каширина
ТЕОРИЯ И ПРАКТИКА ВЕКТОРНОЙ ОПТИМИЗАЦИИ
Учебное пособие
Издательский дом ВГУ
Утверждено учебно-методическим советом факультета прикладной математики, информатики и механики 10 января 2017 г., протокол № 5
Рецензент: декан математического факультета ВГУ, доктор физико-математических наук, профессор А.Д. Баев
В пособии излагается теоретический и практический материал, затрагивающий основные разделы векторной оптимизации. Приведены различные алгоритмы решения задач векторной оптимизации, обоснованные доказательством теорем и проиллюстрированные примерами.
Учебное пособие подготовлено на кафедре математических методов исследования операций факультета ПММ Воронежского государственного университета. Рекомендуется для студентов, обучающихся по направлениям: "Прикладная математика и информатика", "Бизнес-информатика"
СОДЕРЖАНИЕ
| §1. Постановка задачи векторной оптимизации. Принципы оптимальности | |
| §2. Графический метод проверки эффективности точки задач векторной оптимизации | |
| §3.Классификация методов решения ЗВО | |
| §4. Методы решения ЗВМ, основанные на свертывании (скаляризации) критериев | |
| §5.Принцип максимальной эффективности и принцип гарантированного результата | |
| 5.1. Принцип максимальной эффективности и принцип гарантированного результата в случае равнозначных критериев | |
| 5.2. Принцип максимальной эффективности и принцип гарантированного результата при заданном приоритете критериев | |
| §6. Методы решения ЗВМ, основанные на лексикографическом принципе оптимальности | |
| §7. Методы, использующие ограничения на критерии | |
| 7.1. Метод ограничений | |
| 7.2. Метод последовательных уступок | |
| §8. Целевое программирование | |
| §9. Методы решения ЗВМ произвольной структуры | |
| 9.1. Дискретизация множеств | |
| 9.2. Фильтрация множеств | |
| Список литературы |
Постановка задачи векторной оптимизации. Принципы оптимальности
|
|
|
Рассмотрим задачу принятия решений, в которой качество альтернатив множества  (
( – непрерывные выпуклые функции) оценивается набором критериев – непрерывных функций
– непрерывные выпуклые функции) оценивается набором критериев – непрерывных функций  Если цель решения задачи заключается в отыскании такой альтернативы
Если цель решения задачи заключается в отыскании такой альтернативы  , в которой каждый из критериев принимает наибольшее или наименьшее значение, то в этом случае задача математически записывается следующим образом:
, в которой каждый из критериев принимает наибольшее или наименьшее значение, то в этом случае задача математически записывается следующим образом:

 (1)
(1)
и называется задачей векторной оптимизации (ЗВО), а каждая из функций  - частным критерием.
- частным критерием.
Если в исходной задаче критерии однонаправлены, т.е. все критерии, например, стремятся к максимуму (или к минимуму), то задача называется однородной. В противном случае исходная задача – неоднородная задача оптимизации.
Если  – непрерывные, вогнутые функции, а
– непрерывные, вогнутые функции, а 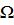 – непустой компакт (замкнутое, выпуклое множество), задача (1) называется задачей выпуклой векторной оптимизации. Именно такие задачи мы преимущественно и будем рассматривать.
– непустой компакт (замкнутое, выпуклое множество), задача (1) называется задачей выпуклой векторной оптимизации. Именно такие задачи мы преимущественно и будем рассматривать.
Если  и
и  линейны, то задача (1) называется задачей линейной векторной оптимизации. Теория решения таких задач разработана наиболее полно.
линейны, то задача (1) называется задачей линейной векторной оптимизации. Теория решения таких задач разработана наиболее полно.
С учетом того, что каждая оптимизированная задача может быть переписана в эквивалентной постановке как задача максимизации критериев, будем для удобства рассматривать задачу векторной максимизации (ЗВМ), записывая её в следующем виде:
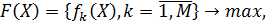
 . (2)
. (2)
Введем в рассмотрение ряд определений, связанных с понятием решения ЗВО.
Определение 1. Вектор  называется идеальным решением задачи векторной оптимизации, если для любого
называется идеальным решением задачи векторной оптимизации, если для любого  выполнены неравенства:
выполнены неравенства: 
|
|
|
Другими словами, идеальное решение задачи (2) является одновременно решением всех M частных задач:

 (3)
(3)
Требования, предъявленные к функциям  и естественное предположение о том, что
и естественное предположение о том, что 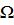 не пусто, обеспечивают существование решения частных задач. Причем, если через
не пусто, обеспечивают существование решения частных задач. Причем, если через  обозначить множество оптимальных точек каждой из частных задач, то
обозначить множество оптимальных точек каждой из частных задач, то
 –
–
множество решений исходной задачи.
Однако на практике критерии  оказываются, как правило, противоречивыми, что приводит к пустому пересечению множеств решений (3) и отсутствию идеального решения. Поэтому формальная запись задачи векторной максимизации не может быть основой для решения. В результате этого считается, что задача векторной оптимизации реализует так называемые априорные рациональные принципы оптимальности, которые полностью определяются описанием множества
оказываются, как правило, противоречивыми, что приводит к пустому пересечению множеств решений (3) и отсутствию идеального решения. Поэтому формальная запись задачи векторной максимизации не может быть основой для решения. В результате этого считается, что задача векторной оптимизации реализует так называемые априорные рациональные принципы оптимальности, которые полностью определяются описанием множества 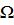 , отображениями
, отображениями  и предпочтительными направлениями изменения оценок
и предпочтительными направлениями изменения оценок  (в нашем случае - максимизация). К таким принципам оптимальности относятся принципы Слейтера и Парето.
(в нашем случае - максимизация). К таким принципам оптимальности относятся принципы Слейтера и Парето.
1.Принцип Слейтера
Определение 2. Точка 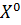 называется оптимальной по Слейтеру в задаче векторной максимизации, если не существует другой точки
называется оптимальной по Слейтеру в задаче векторной максимизации, если не существует другой точки  для которой
для которой 
Множество оптимальных по Слейтеру точек Sl называют множеством слабо эффективных точек.
Другими словами, если ввести множество
 то
то
 .
.
Замечание 1. Любое решение каждой частной задачи (3) является точкой, оптимальной по Слейтеру.
2. Принцип Парето
Определение 3. Точка 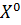 называется оптимальной по Парето в задаче векторной максимизации, если не существует другой точки
называется оптимальной по Парето в задаче векторной максимизации, если не существует другой точки  для которой
для которой  и существует такой индекс
и существует такой индекс  , что
, что 
Множество Парето – оптимальных точек Pr называют множеством эффективных точек.
Другими словами, если ввести множество
 то
то
 .
.
Замечание 2. Отметим, что в множестве решений каждой частной задачи (3) существует непустое подмножество точек, являющихся Парето – оптимальными, что обеспечивает существование решение задачи выбора с принципом Парето. Более того, если решение каждой частной задачи  единственно, то
единственно, то  Таким образом,
Таким образом, 
С понятием решения ЗВО связано понятие доминирования.
Доминирование. Недоминируемые критериальные векторы
|
|
|
Рассмотрим задачу векторной максимизации (2).
Каждой точке  может быть поставлена в соответствие точка
может быть поставлена в соответствие точка  где
где  Тогда Z – элемент из M – мерного евклидова пространства
Тогда Z – элемент из M – мерного евклидова пространства  , которое принято называть критериальным, а его элементы – критериальными векторами.
, которое принято называть критериальным, а его элементы – критериальными векторами.
Множество  называется достижимым множеством.
называется достижимым множеством.
Таким образом, каждой задаче векторной максимизации (2) может быть поставлена в соответствие задача:

 (4)
(4)
Для установления аналогий между решениями задач (2) и (4) введем в рассмотрение следующие определения.
Пусть  – критериальные векторы.
– критериальные векторы.
Определение 4. Вектор  слабо доминирует вектор
слабо доминирует вектор  , если
, если 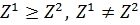 (т. е.
(т. е.  и
и  по крайней мере, для одного k).
по крайней мере, для одного k).
Определение 5. Вектор  сильно доминирует вектор
сильно доминирует вектор  , если
, если  , т. е.
, т. е. 
Определение 6. Критериальный вектор  называется недоминируемым, если не существует другого вектора
называется недоминируемым, если не существует другого вектора  такого, что
такого, что 
Иначе  называется доминируемым.
называется доминируемым.
Определение 7. Критериальный вектор  называется недоминируемым сильно, если не существует другого вектора
называется недоминируемым сильно, если не существует другого вектора  такого, что
такого, что 
В рамках введенных определений Парето – оптимальное множество задачи (2) состоит из таких точек  , критериальные векторы которых являются недоминируемыми, а множество Слейтера включает точки, критериальные векторы которых недоминируются сильно.
, критериальные векторы которых являются недоминируемыми, а множество Слейтера включает точки, критериальные векторы которых недоминируются сильно.
Замечание 3. Соотношения  понимаются выполняемыми покоординатно.
понимаются выполняемыми покоординатно.
Рассмотрим следующие примеры.
Пример 1. Представить графически достижимую область в пространстве критериев для задачи:
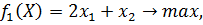


Решение. Допустимое множество задачи представлено на рисунке 1.
Вершинами многогранника  являются следующие точки:
являются следующие точки:


Каждая точка X множества  является выпуклой линейной комбинацией вершин
является выпуклой линейной комбинацией вершин  т.е.
т.е.
 где
где 

Рассмотрим отображение  определяемое правилом:
определяемое правилом:

где 
Отображение F является линейным оператором, и поэтому образ любой точки  является линейной комбинацией образов вершин допустимого множества, т.е.
является линейной комбинацией образов вершин допустимого множества, т.е.  где
где  т.е.
т.е.  является выпуклым многогранником, вершины которого находятся среди точек
является выпуклым многогранником, вершины которого находятся среди точек 
Найдем координаты точки 

 т.е.
т.е. 
Аналогично: 
Достижимое множество в пространстве критериев Q изображено на рисунке 2.
|
|
|
Пример2. Вектор  сильно доминирует вектор
сильно доминирует вектор  и слабо доминирует вектор
и слабо доминирует вектор 

Пример 3. Рассмотрим задачу:



Найти множество оптимальных по Парето и по Слейтеру точек.
Решение. Допустимая область задачи и векторы – градиенты целевых функций представлены на рисунке 3.
Точка  является оптимальной по Парето, так как в допустимом множестве не существует точек X таких, что
является оптимальной по Парето, так как в допустимом множестве не существует точек X таких, что  причем одно из неравенств – строгое. (ABC) – множество оптимальных по Слейтору точек.
причем одно из неравенств – строгое. (ABC) – множество оптимальных по Слейтору точек.

Упражнения к § 1
№ 1. Представьте графически достижимую область в пространстве критериев  для задач:
для задач:
1) 


2) 


3) 


№ 2. Для каждого из перечисленных векторов определите слабо и сильно доминирующие векторы:


№ 3. Определите, какие точки из таблицы эффективны.
| Точки | 
| 
| 
| 
| 
|

| -2 | -5 | |||

| -5 | ||||

| -1 | ||||

| -6 | ||||

| |||||

| -2 | -4 | -1 | -3 | -2 |
|
|
|


