 |
Тестовые задания для контроля конечного уровня знаний
|
|
|
|
Выберите один или несколько правильных ответов
1. ПРИ РАСЧЕТЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ СРЕДНЕЙ И ОТНОСИТЕЛЬНОЙ ВЕЛИЧИНЫ ПРИ ЧИСЛЕ НАБЛЮДЕНИЯ N<30 ДОВЕРИТЕЛЬНЫЙ КОЭФФИЦИЕНТ (T) ОПРЕДЕЛЯЕТСЯ
1) по специальной формуле
2) по таблице со специальным коэффициентом
3) по таблице Стьюдента
4) с помощью коэффициента
2. ЗА УСЛОВНУЮ СРЕДНЮЮ МОЖНО ПРИНЯТЬ
1) моду
2) моду, медиану
3) моду, медиану, любую варианту ряда
4) моду, медиану, любую варианту ряда, любое числовое значение
5) моду, медиану, любую варианту ряда, любое числовое значе ние, доверительный коэффициент.
3. ДЛЯ ОПРЕДЕЛЕНИЯ ОШИБКИ СРЕДНЕЙ ВЕЛИЧИНЫ ПРИ БОЛЬШОМ ЧИСЛЕ НАБЛЮДЕНИЙ ИСПОЛЬЗУЕТСЯ:
1) m = 
2) 
3) m = ± 
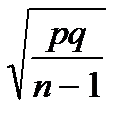4) 
4. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ПО СПОСОБУ МОМЕНТОВ РАВНА:
1) полусумме крайних показателей вариационного ряда
2) любой варианте ряде плюс среднее отклонение от нее всех вариант
3) наименьшей варианте ряда плюс среднее отклонение от нее всех вариант
5. ДЛЯ ВЫЧИСЛЕНИЯ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ВЗВЕШЕННОЙ ПРИМЕНЯЕТСЯ ФОРМУЛА:
1) M = 
2) M = 
3) M = М1 + 
4) M = М1 + i
6. ОШИБКА СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ВЕЛИЧИНЫ ПОКАЗЫВАЕТ
1) в каких пределах могут колебаться полученные средние арифметические величины
2) как отличается максимальный показатель ряда от средней арифметической величины
3) как отличается минимальный показатель ряда от средней арифметической величины
7. ДЛЯ ОЦЕНКИ ДОСТОВЕРНОСТИ РАЗНОСТИ СРАВНИВАЕМЫХ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН ИСПОЛЬЗУЕТСЯ ФОРМУЛА:
1) 
2) t = 
3) t =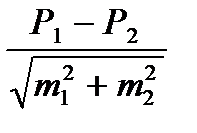 
8. СРЕДНЯЯ ВЕЛИЧИНА-ЭТО:
1) величина, делящаяся вариационный ряд на две равные части
2) варианта, имеющая наибольшее значение
3) средний показатель
4) наиболее часто встречающаяся варианта
|
|
|
5) расчетная величина, дающая обобщающую характеристику изучаемого явления
9. ЦЕЛЬ ВЫЧИСЛЕНИЯ СРЕДНЕКВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ:
1) для оценки отличия условной от средней величины
2) для определения доверительного интервала средней в вариационном ряду
3) для оценки колеблемости средней величины в вариационном ряду
4) для оценки различий между средними, вычисленных разными способами
5) для характеристики дисперсии, или изменчивости признака
10. КАКОЕ ЧИСЛО НАБЛЮДЕНИЙ СООТВЕТСТВУЕТ ТАК НАЗЫВАЕМОЙ МАЛОЙ ВЫБОРКЕ:
1) не более 5
2) меньше 100
3) меньше 30
4) меньше 40
5) меньше 50
11. КАКАЯ ДОЛЯ ВАРИАНТ ПОПАДЕТ В ИНТЕРВАЛ «СРЕДНЯЯ + 2 СИГМЫ»:
1) 95,5%
2) 99,7%
3) 100,0%
4) 68%
5) 90%
12. КАКИЕ ИЗМЕНЕНИЯ СЛЕДУЕТ СДЕЛАТЬ С ЧИСЛОМ НАБЛЮДЕНИЙ В СЛУЧАЕ, ТАК НАЗЫВАЕМОЙ, МАЛОЙ ВЫБОРКИ:
1) разделить на среднюю величину или показатель
2) оставить без изменения
3) вычесть единицу
4) умножить на среднее квадратичное отклонение
5) прибавить единицу
13. ВАРИАЦИОННЫЙ РЯД - ЭТО
1) ряд любых измерений
2) измерения, расположенные в ранговом порядке
3) однородные показатели, изменяющиеся во времени
4) ряд отвлеченных величин
5) ряд элементов статистической совокупности
14. ЦЕЛЬЮ ВЫЧИСЛЕНИЯ СРЕДНЕКВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ЯВЛЯЕТСЯ
1) оценка отличия условной от средней величины
2) определение доверительного интервала средней в вариационном ряду
3) оценка колеблемости средней величины в вариационном ряду
4) оценка различий между средними, вычисленных разными способами
15. МОДА-ЭТО
1) расчетная величина
2) варианта, чаще других встречающаяся
3) варианта, делящая вариационный ряд на две равные части
4) модальный показатель
5) условная средняя
16. МЕДИАНА - ЭТО
1) наибольшее значение и делящая вариационный ряд на
2) две равные части
3) варианта, делящая вариационный ряд на две равные части
4) условная средняя, делящая вариационный ряд на две равные части
|
|
|
5) модальный показатель
17. ПРОЦЕНТНОЕ ОТНОШЕНИЕ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ К СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ - ЭТО
1) ошибка репрезентативности
2) условная средняя
3) доверительный коэффициент
4) коэффициент вариации
5) критерий достоверности разности
18. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ – ЭТО
1) интервал, в пределах которого находятся не менее 68% вариант, близких к средней величине
2) пределы возможных колебаний средней величины (показателя) в генеральной совокупности
3) разница между максимальной и минимальной вариантами вариационного ряда.
Литература
Основная
1.Общественное здоровье и здравоохранение: учебник для студентов под ред.: В. А. Миняева, Н. И. Вишнякова М. – МЕДпресс-информ, 2009. – 655 с.
2.Руководство к практическим занятиям по общественному здоровью и здравоохранению (с применением медицинских информационных систем, компьютерных и телекоммуникационных технологий): учеб. пособие для студентов / И. Н. Денисов, Д. И. Кича, В. И. Чернов. – М.: МИА, 2009. – 464 с.
3.Общественное здоровье и здравоохранение [Электронный ресурс]: учебник для студентов учреждений высш. проф. образования /Ю. П. Лисицын, Г. Э. Улумбекова – М.: ГЭОТАР-МЕДИА, 2011. – 544 с. Режим доступа: http://www.studmedlib.ru/book/ISBN9785970419977.html
Дополнительная
1.Применение методов статистического анализа для изучения общественного здоровья и здравоохранения [Электронный ресурс]: учебное пособие для практ. занятий под ред. В.З. Кучеренко. - М.: ГЭОТАР-Медиа, 2011. - 256 с. – Режим доступа: http://www.studmedlib.ru/book/ISBN9785970419151.html
2.Избранные лекции по общественному здоровью и здравоохранению [Электронный ресурс]: учеб. пособие. - Электрон. текстовые дан. под ред. В. З. Кучеренко М.: Медицина, 2010. – Режим доступа http://www.studmedlib.ru/book/ISBN5225034640.html
Информационный блок
Вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по величине, расположенных в определенном порядке. Вариационный ряд состоит из вариант (V) и соответствующих им частот (Р).
Варианта (V) – это каждое числовое значение изучаемого признака. Частота (Р) – это абсолютная численность отдельных вариант в совокупности, указывающая, сколько раз встречается данная варианта в вариационном ряду.
|
|
|
Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой n.
Вариационный ряд, в котором каждая варианта встречается только один раз (т.е. все Р = 1) называется простым. Если варианты встречаются более одного раза, такой ряд называется взвешенным.
При большом числе наблюдений (более 30) вариационный ряд рекомендуется группировать. Для выбора количества групп в вариационном ряду необходимо учитывать число наблюдений, а также разность между максимальным и минимальным значениями вариант.
Построение из индивидуальных данных вариационного ряда – это только первый шаг к осмысливанию особенностей всей совокупности. Далее необходимо определить средний уровень изучаемого количественного признака. В медицинской статистике широко используются средние величины. Они применяются для характеристики здоровья населения: рождаемости, заболеваемости, инвалидности, смертности, в описании симптомов и течения различных болезней, физического развития отдельных контингентов, при обобщении результатов научных экспериментов. При характеристике организации амбулаторно-поликлинической помощи населению используются такие понятия, как среднее число врачебных посещений на одного жителя в год, средняя численность населения на терапевтическом и педиатрическом участке и т.д. Таким образом, средние величины чрезвычайно широко используются в медицинской статистике.
Средняя - это величина, которая одним числовым значением дает представление обо всей статистической совокупности. Средние величины следует вычислять только на качественно однородном материале. Так, например, при характеристике физического развития новорожденных в исследуемую группу должны быть отобраны младенцы одного пола. Во-вторых, при определении средних величин должно быть достаточное число наблюдений в выборочной совокупности.
Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, мода, медиана и др.
|
|
|
Из этих характеристик в медицинской статистике наиболее часто пользуются средними арифметическими величинами. Средние арифметические величины, в свою очередь, в зависимости от метода расчета делятся на:
· среднюю арифметическую простую,
· среднюю арифметическую взвешенную,
· среднюю арифметическую способом моментов,
· среднюю арифметическую в сгруппированном (интервальном) ряду.
Для расчета средней арифметической величины, прежде всего числовые значения (варианты) располагают в возрастающем или, напротив, в убывающем порядке, т.е. составляют вариационный ряд.
Пример 1. Вычисление средней арифметической простой:
| Vcм | P |
| n=9 |
В простом вариационном ряду средняя арифметическая простая определяется по формуле
cм
Когда отдельные значения вариант начинают повторяться, нужно указать частоту встречаемости (Р) каждой варианты (взвешенный вариационный ряд).
Во взвешенном вариационном ряду среднюю арифметическую можно определить двумя методами: средняя арифметическая «взвешенная» и по способу моментов.
Пример 2. Вычисление средней арифметической «взвешенной».
| Vcм | P | V·P |
| n=73 | ∑VP |
Средняя арифметическая взвешенная определяется по формуле:
cм
Этот способ определения средней величины является неудобным ввиду необходимости проведения больших расчетов и применяется, в основном, при наличии счетной техники.
Следующий способ (способ моментов) более удобен для расчета.
Пример 3. Вычисление средней арифметической способом моментов:
| Vcм | P | а·=(V- М1) | а·Р |
| -9 | - 9 | ||
| -7 | -28 | ||
| -6 | -42 | ||
| -4 | -32 | ||
| -3 | -30 | ||
| 125 | |||
| n =73 | ∑aP=-71 |
В вариационном ряду выбирается варианта, которая наиболее часто встречается (мода) и её принимают за условную среднюю величину (М1). В нашем примере 125. Находим отклонения всех других вариант от условной средней, затем сумму произведений отклонений всех вариант (∑aP) делим на общее число наблюдений (∑aP момент первой степени).
n
Момент первой степени и является той величиной, которая показывает, насколько условная средняя варианта отличается от фактической или истинной средней. Напишем формулу:
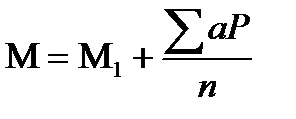
cм
При большом количестве наблюдений число встречающихся размеров вариант может быть очень большим; тогда рекомендуются варианты объединять в группы, причем каждая группа должна иметь равное число значений вариант (иметь равный интервал) 2, 3.... и т.д.
|
|
|
Пример 4. Вычисление средней арифметической в сгруппированном вариационном ряду.
| V1 -V2 (cм) | P | ai | ai·P |
| 110-112 | -4 | - 4 | |
| 113-115 | -3 | -15 | |
| 116-118 | -2 | -22 | |
| 119-121 | -1 | -12 | |
| 122-124 | |||
| 125-127 | |||
| 128-130 | |||
| 131-133 | |||
| n=73 | ∑aiP=-9 |
Условной средней (M1) в сгруппированном вариационном ряду является середина наиболее часто встречающейся группы (122-124), которая определяется в зависимости от изучаемого признака двумя способами:
1. В непрерывном вариационном ряду, когда числовые значения изучаемого признака могут выражаться дробными числами (рост, вес, масса тела, содержание в крови и мочи их ингредиентов и т.д.) как полусумма первых значений смежных (соседних) групп.
2. В дискретном вариационном ряду, когда признаки выражены целыми числами (частота дыхания, пульс, артериальное давление и т.д.) - как полусумма начала и конца наиболее часто встречающейся группы, взятой за условную среднюю.
Наш вариационный ряд непрерывный (рост восьмилетних мальчиков). Поэтому середина равняется М1 = 
см
Отклонения (ai) в сгруппированном вариационном ряду определяем как условные, выраженные в интервальных значениях (при определении отклонения пренебрегаем интервалом).
Для расчета интервал (разница между значениями групп) i используем формулу:
i = Vmax - Vmi n , где n1 – число групп
n1
В нашем примере интервал i = 3 см:
i = 133 - 110 = 2,8 ≈ 3 (года)
Напишем формулу: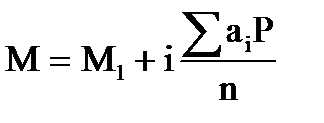 
см
Таким образом, мы рассмотрели четыре способа определения средней арифметической величины: среднюю арифметическую в простом вариационном ряду, во взвешенном вариационном ряду - среднюю арифметическую «взвешенную» и по способу моментов и среднюю арифметическую в сгруппированном вариационном ряду.
Кроме средней арифметической величины в медицинской статистике пользуются модой и медианой.
Модой в вариационном ряду называется варианта, которая среди других встречается наиболее часто. Практическое значение моды заключается в том, что, не проводя порой достаточно сложных расчетов, а, ориентируясь на моду, можно знать примерное значение средней величины.
Медианой называется варианта, делящая вариационный ряд пополам. Практическое значение медианы заключается в том, что в симметричном вариационном ряду, котором в обе стороны от середины находится равное число вариант, она по своему значению наиболее близка к средней величине.
Среднее квадратическое отклонение (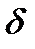
) – степень колеблемости (вариабельности) вариационного ряда, наиболее точно характеризует степень варьирования. Выражается в тех же единицах, что и варианты ряда.
Пример 5. Расчет среднего квадратического отклонения в простом вариационном ряду:
| Vcм | P | d=(V-M) | d2 |
| -6,9 | 47,6 | ||
| -4,9 | 24,0 | ||
| -3,9 | 15,2 | ||
| -1,9 | 3,6 | ||
| -0,9 | 0,8 | ||
| 2,1 | 4,4 | ||
| 4,1 | 16,8 | ||
| 5,1 | 26,0 | ||
| 7,1 | 50,4 | ||
| n=9 | 
|
Последовательность расчета:
1. Находим отклонение (d) каждой варианты от истинной средней (V-M). Для данного вариационного ряда М = 122,9 (пример 1).
2. Отклонение возводим в квадрат (d2).
3. Находим сумму квадратов отклонений (d2).
4. Сумму квадратов отклонений делим на число наблюдений и извлекаем корень квадратный.
Напишем формулу: 
При числе наблюдений n < 30 формула следующая: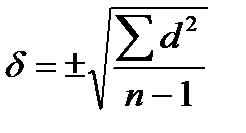 
см
Пример 6. Расчет среднего квадратичного отклонения во взвешенном вариационном ряду (способ среднеарифметический):
| Vсм | P | d | d2 | d2P |
| -8 | ||||
| -6 | ||||
| -5 | ||||
| -3 | ||||
| -2 | ||||
| n=73 | ∑d2P=878 |
Последовательность расчета:
1. Находим отклонения вариант от истинной средней М=124,03 (пример 2). Для упрощения расчетов возьмем М =124 см.
2. Отклонения возводим в квадрат (d2).
3. Квадрат отклонений умножаем на частоту (d2P).
4. Находим сумму квадратов отклонений (
).
5. Сумму квадратов отклонений делим на число наблюдений и извлекаем корень квадратный.
Напишем формулу: 
см
Если средняя арифметическая рассчитывалась по способу моментов. То среднее квадратичное отклонение определяется по следующей методике.
Пример 7. Расчет среднего квадратического отклонения во взвешенном вариационном ряду моментов.
| Vсм | P | a | aP | a2 | a2P |
| -9 | -9 | ||||
| -7 | -28 | ||||
| -6 | -42 | ||||
| -4 | -32 | ||||
| -3 | -30 | ||||
| 125 | |||||
| n=73 | 
| 
|
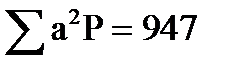
Последовательность расчета:
1 Находим отклонения (а) вариант от условной средней (М1=125).
2.Отклонения умножаем на частоту встречаемости вариант (аP).
3.Находим сумму отклонений (∑aP) и делим на число наблюдений (∑ aP)
n
- момент первой степени.
4.Отклонения возводим в квадрат (а2).
5.Квадрат отклонений умножаем на частоту (а2P).
6.Находим сумму квадратов отклонений (∑a2P) и делим на число наблюдений (∑a2P)
n
- момент второй степени.
7.Из момента второй степени вычитаем момент первой степени, возведенный в квадрат, извлекаем корень квадратный.
Напишем формулу и определим сигму:
cм
При определении средней арифметической величины в сгруппированном вариационном ряду отклонения (а) определяются в условных интервальных отклонениях (пример 4.) Формула расчета среднего квадратичного отклонения в этом случае следующая:
, где
i - интервальное отклонение.
В целях экономии времени, затрачиваемого на расчеты, среднее квадратичное отклонение можно найти упрощенным способом:
, где
К- специальный коэффициент, величина которого определяется числом наблюдений по таблице С.И. Ермолаевой.
Значение К для вычисления квадратичного отклонения(δ) по амплитуде
| - | - | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 | |
| 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3,69 | |
| 3,73 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 | |
| 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,28 | 4,30 | |
| 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 | |
| 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 | |
| 4,64 | 4,65 | 4,66 | 4,68 | 4,69 | 4,70 | 4,71 | 4,72 | 4,73 | 4,74 | |
| 4,75 | 4,77 | 4,78 | 4,79 | 4,80 | 4,81 | 4,82 | 4,83 | 4,83 | 4,84 | |
| 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 | |
| 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 | |
| 5,02 | 5,49 | 5,76 | 5,94 | 6,07 | 6,18 | 6,28 | 6,35 | 6,42 | 6,48 |
Для нашего примера среднее квадратичное отклонение упрощенным методом: δ =± 130-116 =±2,9 см
4,79
|
|
|
