 |
Задание 1. Линейное программирование.
|
|
|
|
1. Решить задачу линейного программирования графически.
2. Привести задачу к каноническому виду и решить её аналитически, симплекс-методом.
3. Указать соответствие между графическим и аналитическим решением.
4. Составить модель двойственной задачи.
5. Используя последнюю симплекс-таблицу найти решение двойственной задачи линейного программирования, проверить правильность решения графически.
6. Проверить выполнение теорем двойственности. Дать экономическую интерпретацию полученного решения.
max f (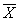
) = 2x1 + 2x2
2x1 + 3x2 
12
2x1 + x2 8
x1, x2 
0
1. Решить задачу линейного программирования графически.
1. Множество решений каждого нестрогого неравенства – объединение решений уравнения и строгого неравенства. Заданы уравнения прямых, для построения каждой прямой достаточно двух точек. Удобно строить прямые по точкам пересечения их с осями координат (когда одна из координат равна нулю).
Найдем точки пересечения прямых с осями координат:
2x1 + 3x2 = 12 x1 = 0, x2 = 12/3=4 Þ (0, 4)
x2 = 0, x1 = 12/2 Þ (6, 0)
2x1 + x2 = 8 x1 = 0, x2 = 8 Þ (0, 8)
x2 = 0, x1 = 8/2 Þ (4, 0)
Если в произвольно взятой точке, не принадлежащей прямой, неравенство выполняется, то оно выполняется и во всех точках той полуплоскости, которой принадлежит контрольная точка, и не выполняется во всех точках другой полуплоскости. В качестве такой точки удобно брать начало координат.
Множество решений 1-го неравенства – полуплоскость, лежащая ниже построенной I-й прямой. Это выясним, взяв контрольную точку, например, (0; 0): 2*0 + 3*0 = 0 < 12.
 |
Множество решений 2-го неравенства – полуплоскость, лежащая ниже построенной II-й прямой. Это выясним, взяв контрольную точку, например, (0; 0): 2*0 + 0 = 0 < 8.
|
|
|
С учетом прямых ограничений х1, x2 
0 получаем многоугольник решений (заштрихованный), обозначим вершины полученного многоугольника решений ABCO. Координаты этих вершин являются допустимыми решениями данной задачи линейного программирования. Их можно определить, решая систему уравнений двух пересекающихся соответствующих прямых.
б) Приравняем целевую функцию F к постоянной величине а:
2x1 + 2x2 = а.
Это уравнение – множество точек, в котором целевая функция принимает значение, равное а. Построим линию уровня при а = 0 (пунктирная прямая): 2x1 + 2x2 = 0.
Точка пересечения этой прямой с осями координат: (0; 0).
При х2 = 1 2*х1 + 2*1 = 0 
х1 = -2/2 = – 1 (– 1, 1).
Для определения направления к оптимуму построим вектор-градиент 
, координаты которого – частные производные функции F, т.е. = (с1; с2) = (2; 2). Для построения соединим точку (2; 2) с началом координат.
Для нахождения максимума целевой функции смещаем линию уровня параллельно самой себе в направлении вектора-градиента. Максимум достигается в точке С – пересечении прямой I и II.
2х1 + 3х2 = 12, 2х1 + 3(8-2х1) = 12, 2х1 – 6х1 +24 = 12, -4х1 = -12, х1 = 3
2х1 + х2 = 8 х2 = 8 – 2х1 х2 = 8 – 2*3= 2
Получили точку С с координатами (3, 2).
max F = 2*3+2*2=10.
2. Привести задачу к каноническому виду и решить её аналитически, симплекс-методом.
Решение. Приведем эту задачу к каноническому виду, введя дополнительные переменные х3, х4
или
Задавая свободным переменным значения х1 = х2 = 0, получим одно из решений данной задачи х1 = 0, х2 = 0, х3 = 12, х4 = 8,, следовательно, задача обладает исходным опорным планом Х=(0; 0; 12; 8), и для нахождения оптимального плана ее можно решить симплексным методом. Решим эту прямую ЗЛП в симплекс-таблицах:
| № итерации | Базис | cj ci | План | Оценка Q | |||||||
| А1 | А2 | А3 | А4 | ||||||||
| А3 | 12/2 = 6 | ||||||||||
| А4 | 8/2 = 4 | ||||||||||
| F(X) = 0 | 
| – 2 | – 2 | ||||||||
|
|
|
В исходной (нулевой) симплекс-таблице в базис всегда вводятся дополнительные векторы, имеющие нулевые коэффициенты. Рассчитаем строку оценок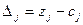 
для каждого столбца А1, А2, А3, А4:
∆1 = 0*2+ 0*2 – 2 = – 2
∆2 = 0 *3+ 0*1 – 2 = – 2
∆3 = 0 * 1+ 0*0 – 0 = 0
∆4 = 0 *0+ 0*1 – 0 = 0
Исходный опорный план Х= (0; 0; 12; 8) не является оптимальным, так как среди оценок есть отрицательные. Переход к новому опорному плану осуществим, введя в базис новой симплекс-таблицы (итерация I) вектор А1, имеющий наименьшую отрицательную оценку ∆1 = –2.
Определим вектор, выходящий из базиса нулевой симплекс-таблицы:
Q = min {6, 4} = 4,
т.е. вектор А4 следует вывести из базиса. Строка А4 будет направляющей строкой, столбец А1 – направляющим столбцом, и на пересечении их будет находиться разрешающий элемент а 21 = 2.
В новой симплекс-таблице (итерация I) в базисе место вектора А4 занимает вектор А1, а вектор А3 остается на своем месте. Столбец А1, соответствующий направляющему столбцу, записывается всегда так: на месте разрешающего элемента пишется единица, а все остальные элементы этого столбца – нули. Заполнение столбцов А2, А3, А4 и В производим с помощью формул (а 21 = 1 - разрешающий элемент).
| № итерации | Базис | cj ci | План | Оценка Q | ||||||
| А1 | А2 | А3 | А4 | |||||||
| I | ←А3 | -1 | 4/2=2 | |||||||
| А1 | 0,5 | 0,5 | 4/0,5=8 | |||||||
| F(X) = 2*2 = 4 |
| -1 | ||||||||
, 
, 
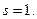
Столбец В: 
, 
,
Строка А1:
, 
, 
.
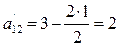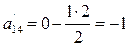Строка А2:
, 
, 
.
Получили еще одно решение задачи: х2 = х4 = 0, т.к. векторов А2, А4 нет в базисе первой итерации, и х1 = 4, х3 = 4, т.к. векторы А1 и А3 находятся в базисе и им соответствуют значения плана В (4; 4), значит, задача обладает новым опорным планом Х=(4; 0; 4; 0).
Рассчитаем строку оценок 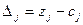для каждого столбца А1, А2, А3, А4:
∆1 = 0*4+ 2*1 – 2 = 0
∆2 = 0 *2+ 2*0,5 – 2 = -1
∆3 = 0 * 1+ 2*0 – 0 = 0
∆4 = 0 *(-1)+ 2*1 – 0 = 2
Найденный опорный план Х=(4; 0; 4; 0) не является оптимальным, так как среди оценок есть отрицательные.
Переход к новому опорному плану осуществим, введя в базис новой симплекс-таблицы (итерация II) вектор А3, имеющий наименьшую отрицательную оценку ∆2 = –1.
Определим вектор, выходящий из базиса нулевой симплекс-таблицы:
Q = min {2, 8} = 2,
т.е. вектор А3 следует вывести из базиса. Строка А3 будет направляющей строкой, столбец А1 – направляющим столбцом, и на пересечении их будет находиться разрешающий элемент а 12 = 2.
|
|
|
В новой симплекс-таблице (итерация II) в базисе место вектора А3 занимает вектор А2, а вектор А1 остается на своем месте. Столбец А2, соответствующий направляющему столбцу, записывается всегда так: на месте разрешающего элемента пишется единица, а все остальные элементы этого столбца – нули. Заполнение столбцов А1, А3, А4 и В производим с помощью формул (а 12 = 2 - разрешающий элемент).
| № итерации | Базис | cj ci | План | Оценка Q | ||||||
| А1 | А2 | А3 | А4 | |||||||
| II | А2 | 0,5 | -0,5 | |||||||
| А1 | -0,25 | 0,75 | ||||||||
| F(X) = 2*3+2*2 = 10 |
| 0,5 | 0,5 | |||||||
, ,
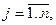
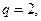
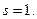
Столбец В: 
, 
,
Строка А1:
, 
, 
.
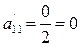Строка А2:
, 
, 
.
Получили еще одно решение задачи: х3 = х4 = 0, т.к. векторов А3, А4 нет в базисе первой итерации, и х1 = 3, х2 = 2, т.к. векторы А1 и А2 находятся в базисе и им соответствуют значения плана В (3; 2), значит, задача обладает новым опорным планом Х=(3; 2; 0; 0).
Рассчитаем строку оценок 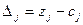для каждого столбца А1, А2, А3, А4:
∆1 = 2*0+ 2*1 – 2 = 0
∆2 = 2 *1+ 2*0 – 2 = 0
∆3 = 2 * 0,5+ 2*(-0,25) – 0 = 0,5
∆4 = 2 *(-0,5)+ 2*0,75 – 0 = 0,5
Найденный опорный план Х=(3; 2; 0; 0) является оптимальным, так как среди оценок нет отрицательных.
Находим оптимум целевой функции:
max f(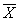) = 2 x1 + 2 x2 = 2*3 + 2*2 = 10.
3. Указать соответствие между графическим и аналитическим решением.
Видим, что графическое решение и аналитическое совпадают.
4. Составить модель двойственной задачи.
Найдем двойственные оценки.
Расширенная матрица коэффициентов при неизвестных в системе ограничений исходной задачи аij и свободных членов bi; коэффициенты целевой функции:
Транспонируя данную матрицу, получим коэффициенты для системы ограничений двойственной задачи:
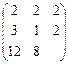
В результате получим искомую двойственную задачу:
Для нахождения оценок у1, у2 используем последнюю симплекс-таблицу.
| № итерации | Базис | cj | План | Оценка Q | ||||||
| ci | А1 | А2 | А3 | А4 | ||||||
| II | А2 | 0,5 | -0,5 | |||||||
| А1 | -0,25 | 0,75 | ||||||||
  F(X) = 10
|
| 0,5 | 0,5 | |||||||
|
|
|
у1 = 0,5,
у 2 = 0,5,
Т.е. у1* = 0,5, у2* = 0,5.
Вычислим значение целевой функции двойственной задачи:
Z(0,5; 0,5)= 12*0,5+8*0,5 =6+4 = 10.
По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.
Экономико-математический анализ оптимальных решений базируется на свойствах двойственных оценок.
1. Величина двойственной оценки того или иного ресурса показывает насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу (двойственные оценки измеряют эффективность малых приращения объемов ресурсов в конкретных условиях данной задачи).
В задаче увеличение ресурса I вида на 1 ед. привело бы к росту максимальной суммы прибыли на 0,5 у.е. (у1=0,5), а увеличение ресурса II вида привело бы к росту максимальной суммы прибыли на 0,5 у.е. (у2=0,5).
2. Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем не дефицитными (избыточны).
В задаче оба ресурса одинаково дефицитны, поскольку у2=0,5 = y1 = 0,5.
Ответ: Х* = (3; 2; 0; 0) – оптимальный план.
Двойственные оценки: Y* = (0,5; 0,5)
Оптимумы целевых функций совпадают Max f(
) = min Z(
) = 10
Экономическая интерпретация оптимальных решений взаимодвойственных задач: предприятию безразлично, производить ли продукцию по оптимальному плану () и получить максимальную прибыль или продать ресурсы по оптимальным ценам (
) и возместить от продажи равные ей минимальные затраты на ресурсы.
Задание 2. Матричные игры
1. Задана платёжная матрица матричной игры с нулевой суммой. Найти верхнюю и нижнюю чистую цену игры.
2. Произвести все возможные упрощения платёжной матрицы.
3. Свести матричную игру к паре двойственных задач линейного программирования и найти решение задачи на минимум в смешанных стратегиях (использовать M-метод).
4. Решить матричную игру графически.
| -1 | -2 | ||||
| -1 | |||||
| -1 |
Решение.
1. Задана платёжная матрица матричной игры с нулевой суммой. Найти верхнюю и нижнюю чистую цену игры.
1) Для определения максиминной и минимаксной стратегии предприятий вычислим для каждой строки матрицы минимальные элементы, а для каждого столбца матрицы − максимальные элементы. Получим:
|
|
|
| В1 | В2 | В3 | В4 | В5 | В6 | min | ||
| A1 | -1 | -2 | -2 | |||||
| A2 | ||||||||
| A3 | ||||||||
| A4 | ||||||||
| A5 | -1 | -1 | ||||||
| A6 | -1 | -1 | ||||||
| max |
Выберем наибольший из минимальных элементов строк. Это будет число 3. Итак, максимин будет равен max(min a ij) = 3, а максиминной стратегией игрока A является стратегия А4. Выберем наименьший из максимальных элементов столбцов. Это будет число 4. Итак, минимакс будет равен min(max a ij) = 4, а минимаксной стратегией игрока B является стратегия B3.
2. Произведем все возможные упрощения платёжной матрицы.
Заметим, что элементы 3-ой строки матрицы превосходят соответствующие элементы 1-й и 2-ой строки, т.е. 3-я строка является доминирующей над 1-й и 2-ой строками, поэтому 1-ю и 2-ю строки опускаем.
Заметим, что элементы 4-ой строки матрицы превосходят соответствующие элементы 5-й и 6-ой строки, т.е. 4-я строка является доминирующей над 5-й и 6-ой строками, поэтому 5-ю и 6-ю строки опускаем.
Далее замечаем, что элементы 1-ого, 2-ого и 5-ого столбцов матрицы превосходят соответствующие элементы 3-го столбца, поэтому 1-й, 2-й и 5-й столбцы опускаем.
3. Свести матричную игру к паре двойственных задач линейного программирования и найти решение задачи на минимум в смешанных стратегиях (использовать M-метод).
Решим матричную игру, сведя матричную игру к паре двойственных задач линейного программирования.
Составим математическую модель.
φ = х1 + х2 + х3 → max.
Составим модель двойственной задачи:
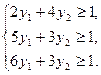
f = y1 + y2 → min.
Найти решение задачи на минимум в смешанных стратегиях.
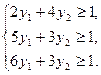
f = y1 + y2 → min.
Для использования данного симплекс-метода будем искать максимум функции g(Х). Помножим неравенства на – 1, чтобы поменять знаки на противоположные, и приведем ЗЛП к каноническому виду, введя дополнительные переменные х4, х5, х6, и искусственные переменные х7, х8 и х9, чтобы знаки последних переменных в левой части и правой части всех неравенств были одинаковые
Приведем эту задачу к каноническому виду, введя дополнительные переменные х3, х4
Если не ввести искусственные переменные во все уравнения, то в базисном решении будут отрицательные компоненты. Задавая свободным переменным значения х1 = х2 = х3 = х4 = х5 = 0, получим одно из решений данной задачи х1 = 0, х2 = 0, х3 = 0, х4 = 0, х5 = 0, х6 = 1, х7 = 1, х8 = 1, следовательно, задача обладает исходным опорным планом Х=(0; 0; 0; 0; 0; 1; 1; 1), и для нахождения оптимального плана ее можно решить симплексным методом. Решим эту прямую ЗЛП в симплекс-таблицах:
| № итерации | Базис | cj ci | План | -1 | -1 | М1 | М2 | М3 | Оценка Q | |||||
| А1 | А2 | А3 | А4 | A5 | А6 | А7 | А8 | |||||||
| А6 | М1 | -1 | 1/2 | |||||||||||
| А7 | М2 | -1 | 1/5 | |||||||||||
| А8 | М3 | -1 | 1/6 | |||||||||||
| F(X) = М1+М2+М3 |
| 2М1+ 5М2+ 6М3+1 | 4М1 + 3М2+ 3М3+1 | -М1 | -М2 | -М3 | ||||||||
В исходной (нулевой) симплекс-таблице в базис всегда вводятся дополнительные векторы, имеющие нулевые коэффициенты. Рассчитаем строку оценок 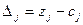для каждого столбца А1, А2, А3, А4:
∆1 = 2М1+5М2 + 6М3+1
∆2 = 4М1 +3М2+3М3+1
∆3 = М 1*(-1)+ М2*0+М3*0 – 0 = –М1
∆4 = М 1*0+ М2*(-1)+М3*0 – 0 = –М2
∆5 = М 1*0+ М2*0+М3*(-1) – 0 = –М3
Исходный опорный план Х=(0; 0; 0; 0; 0; 1; 1; 1) не является оптимальным, так как среди оценок есть отрицательные. Переход к новому опорному плану осуществим, введя в базис новой симплекс-таблицы (итерация I) вектор А1, имеющий наименьшую отрицательную оценку ∆1.
Определим вектор, выходящий из базиса нулевой симплекс-таблицы:
Q = min {1/2, 1/5, 1/6} = 1/6,
т.е. вектор А8 следует вывести из базиса. Строка А8 будет направляющей строкой, столбец А1 – направляющим столбцом, и на пересечении их будет находиться разрешающий элемент а 31 = 6.
В новой симплекс-таблице (итерация I) в базисе место вектора А8 занимает вектор А1, а вектора А6 и А7 остаются на своем месте. Столбец А1, соответствующий направляющему столбцу, записывается всегда так: на месте разрешающего элемента пишется единица, а все остальные элементы этого столбца – нули. Заполнение столбцов А2, А3, А4 и В производим с помощью формул (а 31 = 6 - разрешающий элемент).
| № итерации | Базис | cj ci | План | -1 | -1 | М1 | М2 | Оценка Q | ||||||
| А1 | А2 | А3 | А4 | A5 | А6 | А7 | ||||||||
| I | А6 | М1 | 2/3 | -1 | 1/3 | 2/9 | ||||||||
| А7 | М2 | 1/6 | 1/2 | -1 | 5/6 | 1/3 | ||||||||
| А1 | -1 | 1/6 | 1/2 | -2/3 | 1/3 | |||||||||
| F(X) = 2/3М1+1/6М2 -1/6 |
| 3М1 + 1/2М2- 1/2+1 | -М1 | -М2 | 1/3М1 + 5/6М2+2/3 | |||||||||
Получили еще одно решение задачи: х2 = х3 = х4 = х5 = 0, т.к. векторов А2, А3, А4, А5 нет в базисе первой итерации, и х1 = 1/6, х6 = 2/3, х7 = 1/3, т.к. векторы А1, А6 и А7 находятся в базисе и им соответствуют значения плана В (1/6; 2/3; 1/6), значит, задача обладает новым опорным планом Х=(1/6; 0; 0; 0; 0; 2/3; 1/6).
Найденный опорный план не является оптимальным, так как среди оценок есть отрицательные. Переход к новому опорному плану осуществим, введя в базис новой симплекс-таблицы (итерация II) вектор А2, имеющий наименьшую отрицательную оценку ∆2.
Определим вектор, выходящий из базиса нулевой симплекс-таблицы:
Q = min {2/9, 1/3, 1/3} = 2/9,
т.е. вектор А6 следует вывести из базиса. Строка А6 будет направляющей строкой, столбец А2 – направляющим столбцом, и на пересечении их будет находиться разрешающий элемент а 12 = 3.
В новой симплекс-таблице (итерация II) в базисе место вектора А6 занимает вектор А2, а вектора А1 и А7 остаются на своем месте. Столбец А2, соответствующий направляющему столбцу, записывается всегда так: на месте разрешающего элемента пишется единица, а все остальные элементы этого столбца – нули. Заполнение столбцов А3, А4, А5, А7 и В производим с помощью формул (а 12 = 3 - разрешающий элемент).
| № итерации | Базис | cj ci | План | -1 | -1 | М2 | Оценка Q | |||
| А1 | А2 | А3 | А4 | A5 | А7 | |||||
| II | А2 | -1 | 2/9 | -1/3 | 1/9 | |||||
| А7 | М2 | 5/90 | 1/6 | -1 | 7/9 | 5/70 | ||||
| А1 | -1 | 5/90 | 1/6 | -2/9 | ∞ | |||||
| F(X) = 2/3М1+1/6М2 -1/6 |
| 1/6+М2 | -М2 | 1/3М1 + 5/6М2+2/3 |
Получили еще одно решение задачи: х3 = х4 = х5 = 0, т.к. векторов А3, А4, А5 нет в базисе первой итерации, и х1 = 5/90, х2 = 2/9, х7 = 5/90, т.к. векторы А1, А2 и А7 находятся в базисе и им соответствуют значения плана В (5/90; 2/9; 5/90), значит, задача обладает новым опорным планом Х=(5/90; 2/9; 0; 0; 0; 5/90).
Найденный опорный план не является оптимальным, так как среди оценок есть отрицательные. Переход к новому опорному плану осуществим, введя в базис новой симплекс-таблицы (итерация III) вектор А5, имеющий наименьшую отрицательную оценку ∆5.
Определим вектор, выходящий из базиса нулевой симплекс-таблицы:
Q = min {2, 5/70, ∞} = 5/70,
т.е. вектор А7 следует вывести из базиса. Строка А7 будет направляющей строкой, столбец А5 – направляющим столбцом, и на пересечении их будет находиться разрешающий элемент а 25 = 7/9.
В новой симплекс-таблице (итерация III) в базисе место вектора А7 занимает вектор А5, а вектора А1 и А2 остаются на своем месте. Столбец А5, соответствующий направляющему столбцу, записывается всегда так: на месте разрешающего элемента пишется единица, а все остальные элементы этого столбца – нули. Заполнение столбцов А3, А4 и В производим с помощью формул (а 25 = 7/9 - разрешающий элемент).
| № итерации | Базис | cj ci | План | -1 | -1 | Оценка Q | |||
| А1 | А2 | А3 | А4 | A5 | |||||
| III | А2 | -1 | 3/14 | -5/14 | 1/7 | ||||
| А5 | 5/70 | 3/14 | -9/7 | ||||||
| А1 | -1 | 5/70 | 3/14 | -2/7 | |||||
| F(X) = -3/14- 5/70 = -2/7 |
| 1/7 |
Получили еще одно решение задачи: х4 = х3 = 0, т.к. векторов А4, А3 нет в базисе первой итерации, и х1 = 5/70, х2 = 3/14, х5 = 5/70, т.к. векторы А1, А2 и А5 находятся в базисе и им соответствуют значения плана В (5/70; 3/14; 5/70), значит, задача обладает новым опорным планом Х=(5/70; 3/14; 0; 0; 5/70).
Найденный опорный план является оптимальным, так как среди оценок нет отрицательных.
Находим оптимум целевой функции:
min f(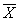) = - max g(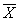) = - (x1 + x2) = - (- 2/7) = 2/7.
4. Решить матричную игру графически.
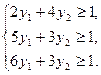
f = y1 + y2 → min.
Область допустимых решений – неограниченна (заштрихована на рисунке).
Граничными точками являются А(0; 1/3), В (5/70; 3/14) и С (1/2; 0).
Построив вектор-градиент получаем оптимальное решение – точку В.
Оптимальным является решение в точке В(5/70; 3/14).
Значение целевой функции в точке В равно f = 5/70 + 3/14 = 2/7
|
|
|
