 |
Свободные незатухающие колебания
|
|
|
|
Колебания системы, выведенной из положения равновесия и далее предоставленной самой себе, называются свободными. В этом случае при отстутствии сил сопротивления уравнение движения имеет вид:
. (3)
Действующая сила пропорциональна смещению (k – коэффициент пропорциональности, а в случае пружинного маятника, коэффициент жесткости пружины) и всегда направлена к положению равновесия. Такой силой является, например, сила упругости. Любая другая сила, неупругая по природе, но удовлетворяющая соотношению F = – kx, называется квазиупругой.
Решение уравнения (3) имеет вид
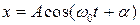, (4)
где x – величина, периодически меняющаяся во времени (для механических колебаний это смещение точки от положения равновесия); А – модуль ее максимального значения (амплитуда); t – время; 
– фаза колебаний; 
– циклическая (собственная или круговая) частота; α – начальная фаза.
Простейший вид колебаний, происходящих по закону косинуса или синуса, называется гармоническими, а система в этом случае называется гармоническим осциллятором.
Скорость и ускорение гармонического осциллятора находят, взяв первую, а затем вторую производные от смещения x:
, (5)
(6)
Тогда сила
(7)
При гармонических колебаниях происходят периодические взаимные превращения энергии, в частности, для механической системы – превращения кинетической энергии в потенциальную.
W пот= 
= 
, (8)
W кин = 
= 
. (9)
Полная энергия гармонического осциллятора:
W полн = W кин + W пот = 
. (10)
Пружинный маятник – система, состоящая из груза массы m, прикрепленного к пружине, массой которой можно пренебречь по сравнению с массой груза. Уравнение движения этой системы (по II закону Ньютона): 
, или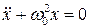 
, где циклическая частота и период:
|
|
|
; 
, (11)
а решение этого дифференциального уравнения имеет вид
.
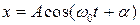Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая движение по дуге окружности в вертикальной плоскости под действием силы тяжести. Уравнение движения этой системы на основании основного уравнения динамики вращательного движения имеет вид: 
. Для случая малых колебаний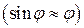 
уравнение принимает вид 
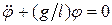. Решением его является функция
, (12)
где 
– амплитуда колебаний, т.е. наибольший угол, на который отклоняется маятник, а циклическая частота и период колебаний:
, 
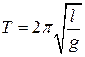. (13)
Физический маятник – твердое тело, совершающее колебания вокруг горизонтальной оси, проходящей через точку подвеса, расположенную выше его центра масс. Уравнение движения этого тела имеет вид: 
(
– момент инерции маятника относительно оси, проходящей через точку подвеса). Для случая малых колебаний уравнение 
имеет решение
,
где циклическая частота и период колебаний:
, 
. (14)
Приведенная длина физического маятника (
) – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника:
. (15)
При сложении двух гармонических колебаний одного направления и одинаковой частоты 
и 
получается гармоническое колебание 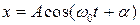, где амплитуда результирующего колебания находится из выражения:
, (16)
а начальная фаза – из выражения:
. (17)
При сложении двух взаимно перпендикулярных колебаний, заданных уравнениями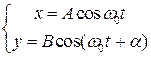 
где 
имеет смысл разности фаз складываемых колебаний в общем случае движение происходит по кривой, уравнений которой имеет вид:
. (18)
Это уравнение эллипса, оси которого повернуты относительно координатных осей. В зависимости от разности фаз могут быть следующие частные случаи:
1). 
. Результирующее движение происходит по прямой 1 на рисунке, уравнение которой
|
|
|
, (19)
с частотой и амплитудой, равной 
.
2). 
. Результирующее движение происходит по прямой 2, уравнение которой
, (20)
с частотой и амплитудой, равной .
3). 
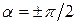. Траектория результирующего движения – эллипс (кривая 3), приведенный к главным осям, уравнение которого имеет вид
. (21)
Полуоси эллипса равны соответствующим амплитудам колебаний А и В.
При А = В эллипс вырождается в окружность (кривая 
).
|
|
|
