11.Матрицы смежности и инцидентности, их основные свойства. Смежностные (реберные) графы.

11. Матрицы смежности и инцидентности, их основные свойства. Смежностные (реберные) графы.

Определим матрицу смежности как симметричную квадратную матрицу А=[a_{i, j}] порядка п, в которой элемент Cjj равен 1, если в графе есть ребро {vi, Vj}, т. е. Vi и Vj смежны, и 0, если такого ребра нет.

Из определения следует, что 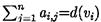при любом i,  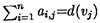при любом j и , т. е. коли­чество единиц в любой строке или столбце матрицы смежнос­ти равно степени соответствующей вершины графа, а общее количество единиц равно удвоенному числу его ребер.

Очевидно, что матрица смежности пустого графа состо­ит из одних нулей, т. е. А(О_п)=0. Матрица смежности полно­го графа состоит из одних единиц, кроме диагональных эле­ментов, которые равны 0.

Также неориентированный граф G может быть полностью описан с помощью его матрицы инцидентности. Определим матрицу инцидент­ности графа как прямоугольную матрицу В=[b_{i, j}] размера n× m, в которой элемент bij равен 1, если вершина v_iинци­дентна ребру e_j, и 0 в противном случае.

Как следует из определения, общее количество единиц в матрице инцидентности равно удвоенному числу ребер гра­фа, количество единиц в любой строке равно степени соот­ветствующей вершины, а столбцы содержат по две единицы. Поэтому между строками матрицы существует простая зави­симость: элементы любой строки могут быть получены сложе­нием одноименных элементов остальных строк по модулю 2. Используя понятие вектора инцидентности, можно записать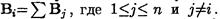

Построение графа можно проводить, начиная с 0-графа (или любого другого), путем добавления нужных вершин и ребер, а также, исходя из полного графа (или любого другого), путем удаления нужных вершин и ребер.

Смежностные (реберные) графы.

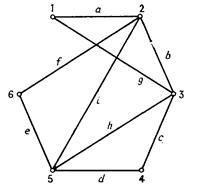
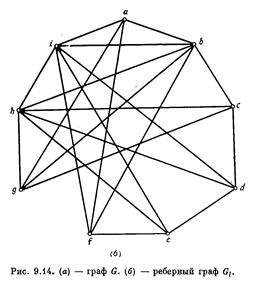
Если рассматривать матрицу смежности ребер как матрицу смежности вершин, то можно получить смежностный или рёберный или покрывающий граф. Такой переход соответствует преобразованию ребра в вершину

Реберный граф L(G) простого графа G — это такой граф, в котором вершины сопоставлены рёбрам G. Вершины в L(G) смежные, если соответствующие им рёбра в G смежные.

Для построения смежностного графа поставим в середине каждого ребра исходного графа точки. Это — вершины смежностного графа. Соединим полученные вершины между собой, если они лежат на смежных ребрах.

12. Изоморфизм графов.

Имеются изобра­жения графов одного порядка с одинаковым числом ребер. Не­обходимо установить, разные это графы или один, только по-разному представленный. Чтобы различать подобные ситуа­ции используют понятие изоморфизма.

Изоморфизмом называют взаимно-однозначное соответ­ствие между множествами вершин двух графов G₁ и G₂, сохраняющее отношение смежности, а сами графы называ­ют изоморфными. Отображая это, пишут: G₁=G

Изоморфизм графов есть отношение эквивалентности. Действительно, изомор­физм обладает всеми необходимыми свойствами:

. 1. рефлексивность: G ~ G, где требуемая биекция суть тождественная функция;

2. симметричность: если G₁ ~ G₂ с биекцией h, то G₂ ~ G₁ с биекцией h^-1;

3. транзитивность: если G₁ ~ G₂ с биекцией h и G₂ ~ Сз с биекцией g, то G₁ ~ Сз с биекцией g h.

Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма