 |
Характеристики – линии распространения разрывов производных решений интегрального аналога (1.56) волнового уравнения (линии слабого разрыва).
|
|
|
|
Т. о., если у решений линеаризованной системы уравнений квазиодномерной ( ) газовой динамики имеют место быть сильные разрывы, то они распространяются только по характеристикам семейств.
Выпишем теперь условия, которым должны удовлетворять скачки 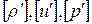 на разрывах:
на разрывах:
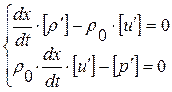 , где
, где 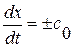 (1. 52. 22)
(1. 52. 22)
Система (1. 52. 2) может быть преобразована к эквивалентной форме, левые части которой имеют важное значение для дальнейшего анализа течений с малыми возмущениями параметров газа:
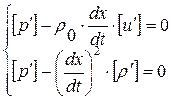 , где
, где 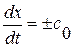 (1. 52. 23)
(1. 52. 23)
или
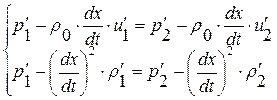 , где
, где 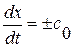 (1. 52. 24)
(1. 52. 24)
Смысл первого из соотношений (1. 52. 4) состоит в инвариантности величины 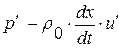 при переходе через сильный разрыв
при переходе через сильный разрыв 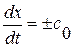 и более подробно будет обьяснен чуть позже. Второе же соотношение в (1. 52. 4), если вспомнить вид линеаризованного уравнения состояния
и более подробно будет обьяснен чуть позже. Второе же соотношение в (1. 52. 4), если вспомнить вид линеаризованного уравнения состояния
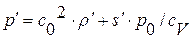 термически и калорически совершенного газа, дает, что
термически и калорически совершенного газа, дает, что 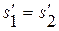 . Т. е. энтропия непрерывна на сильном разрыве или, другими словами, является инвариантом. Заметим, что в полной нелинейной постановке такого свойства не наблюдается, т. е. энтропия разрывна на сильных скачках и поэтому уравнения состояния газа слева и справа от разрыва отличаются в виду различия величины энтропии
. Т. е. энтропия непрерывна на сильном разрыве или, другими словами, является инвариантом. Заметим, что в полной нелинейной постановке такого свойства не наблюдается, т. е. энтропия разрывна на сильных скачках и поэтому уравнения состояния газа слева и справа от разрыва отличаются в виду различия величины энтропии  в выражении
в выражении 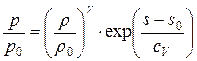 . В нашем же линейном случае мы вправе работать с уравнением состояния для газа одного и того же вида по обе стороны от сильного разрыва.
. В нашем же линейном случае мы вправе работать с уравнением состояния для газа одного и того же вида по обе стороны от сильного разрыва.
Теперь, после такого продолжительного отступления, вернемся на наш второй путь – путь изменения формы записи волнового уравнения с целью понижения уровня требований к дифференцируемости входящей в него функции. Для построения интегрального аналога полученного ранее волнового уравнения для потенциала скорости 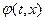 существуют два способа. Первый способ аналогичен выполненной нами ранее линеаризации дифференциальной системы уравнений (1. 13. 1)-(1. 13. 3), но теперь предстоит выполнить линеаризацию уравнений (1. 52. 4)-(1. 52. 6) в интегральной форме записи. Этот способ достаточно громоздок по сравнению со вторым способом, когда из дифференциальной формы записи волнового уравнения путем интегрирования по времени и пространству мы получим интегральный аналог волнового уравнения, не требующий от искомого потенциала
существуют два способа. Первый способ аналогичен выполненной нами ранее линеаризации дифференциальной системы уравнений (1. 13. 1)-(1. 13. 3), но теперь предстоит выполнить линеаризацию уравнений (1. 52. 4)-(1. 52. 6) в интегральной форме записи. Этот способ достаточно громоздок по сравнению со вторым способом, когда из дифференциальной формы записи волнового уравнения путем интегрирования по времени и пространству мы получим интегральный аналог волнового уравнения, не требующий от искомого потенциала 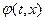 быть дважды дифференцируемым. Итак, проинтегрируем обе части волнового уравнения
быть дважды дифференцируемым. Итак, проинтегрируем обе части волнового уравнения  , выполненного во всех точках верхней полуплоскости
, выполненного во всех точках верхней полуплоскости 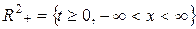 , по области прямоугольной формы
, по области прямоугольной формы 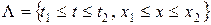 и получим
и получим 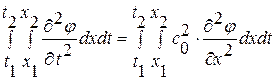 (1. 53. 1)
(1. 53. 1)
|
|
|
 преобразуем полученное интегральное уравнение, взяв соответствующие однократные интегралы (фактически выполнив переход от интегрирования по области
преобразуем полученное интегральное уравнение, взяв соответствующие однократные интегралы (фактически выполнив переход от интегрирования по области  к интегрированию по границе области
к интегрированию по границе области  (Рис. 2. 2). ), и перенесем все члены в левую часть
(Рис. 2. 2). ), и перенесем все члены в левую часть
Рис. 2. 2
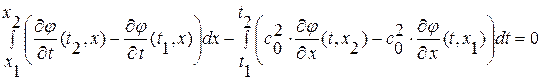
Далее, умножим обе части на “-1”, перегруппируем слагаемые и, поменяв местами в двух последних интегралах пределы интегрирования, получим:
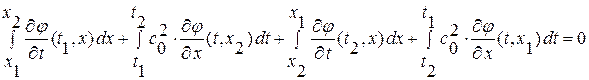
теперь, добавив к каждой из подынтегральных функций слагаемое равное нулю для данного пути интегрирования, получим интеграл по контуру  (контур обходится против часовой стрелки, поэтому-то в интегралах и был изменен порядок пределов интегрирования) от общей подынтегральной функции
(контур обходится против часовой стрелки, поэтому-то в интегралах и был изменен порядок пределов интегрирования) от общей подынтегральной функции 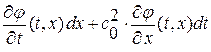 :
:
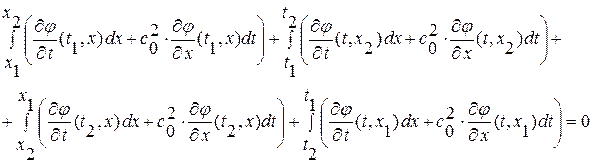
и далее, переписав полученное интегральное уравнение в более компактном виде, имеем
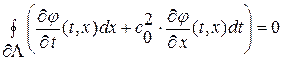 (1. 53. 2)
(1. 53. 2)
|
|
|
Интеграл по контуру  (1. 53. 2) был получен указанным выше способом из интеграла по области
(1. 53. 2) был получен указанным выше способом из интеграла по области  (1. 53. 1), который для удобства дальнейшего применения перепишем в виде:
(1. 53. 1), который для удобства дальнейшего применения перепишем в виде:
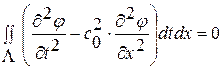 (1. 53. 3)
(1. 53. 3)
Полученный интеграл (1. 53. 2) вместе с (1. 53. 3) – это частный случай формулы Грина для плоской области прямоугольной формы. В общем виде формула Грина для плоской области преобразует двойной интеграл по области  в криволинейный интеграл по границе
в криволинейный интеграл по границе  (причем криволинейный интеграл по границе
(причем криволинейный интеграл по границе  берется в положительном направлении, т. е. с направлением обхода против часовой стрелки Рис. 2. 2):
берется в положительном направлении, т. е. с направлением обхода против часовой стрелки Рис. 2. 2):
 , (1. 54)
, (1. 54)
эта формула справедлива, если область  - односвязная, граница
- односвязная, граница  - непрерывная кусочно-гладкая функция, а функции
- непрерывная кусочно-гладкая функция, а функции 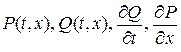 непрерывны на
непрерывны на  .
.
Применяя формулу Грина (1. 54) с указанными ограничениями на область, границу и функции для нашего волнового уравнения получим:
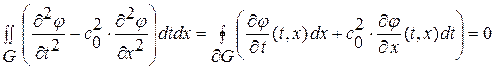 , (1. 55)
, (1. 55)
Сформулируем интегральный аналог задачи Коши для волнового уравнения на неограниченной прямой  :
:
Найти функцию 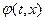 , определенную и кусочно-гладкую в области
, определенную и кусочно-гладкую в области 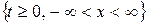 , удовлетворяющую интегральному уравнению
, удовлетворяющую интегральному уравнению
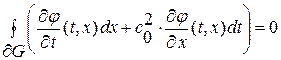 (1. 56)
(1. 56)
и начальным условиям 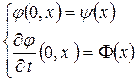 , где функции
, где функции 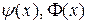 - кусочно-непрерывны. Контур
- кусочно-непрерывны. Контур  - произвольный кусочно-гладкий контур, лежащий в области
- произвольный кусочно-гладкий контур, лежащий в области 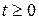 .
.
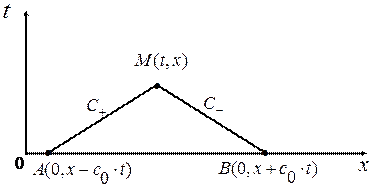 Решение: Пусть функция
Решение: Пусть функция 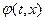 представляет решение задачи. Тогда, выбрав в качестве контура
представляет решение задачи. Тогда, выбрав в качестве контура  треугольник АВМ, образованный отрезками АМ и МВ двух характеристик
треугольник АВМ, образованный отрезками АМ и МВ двух характеристик  и
и 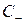 плюс отрезок АВ оси
плюс отрезок АВ оси  , заключенный между характеристиками (Рис. 2. 3),
, заключенный между характеристиками (Рис. 2. 3),
Рис. 2. 3
получим:
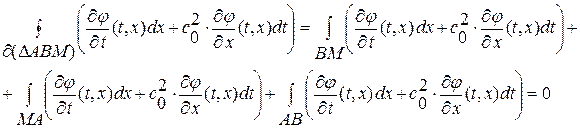 (1. 57)
(1. 57)
Вычислим интегралы вдоль отрезков прямых ВМ, МА, АВ. Для этого заметим, что вдоль отрезка МА ввиду определения характеристики 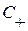 имеет место равенство
имеет место равенство 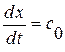 , т. е.
, т. е.
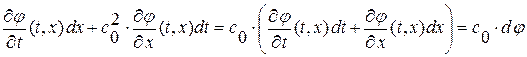 , аналогично
, аналогично
вдоль отрезка ВМ ввиду опред. характеристики  имеет место равенство
имеет место равенство 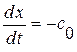 , т. е.
, т. е. 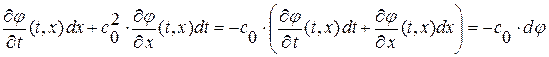 .
.
След., подынтегральное выражение вдоль характеристик является полным дифференциалом. Производя искомое интегрирование вдоль отрезков ВМ и МА, получаем: 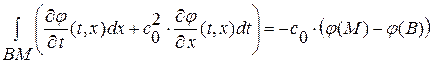 ,
,
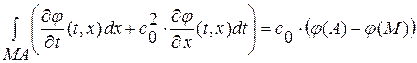 ,
,
|
|
|
далее 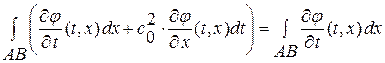 ,
,
поэтому формула (1. 57) примет вид: 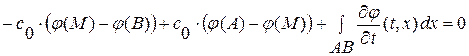 , разрешая которую относительно искомого значения
, разрешая которую относительно искомого значения 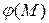 находим:
находим:
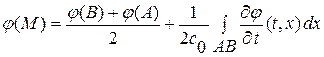 или в исходных переменных
или в исходных переменных 
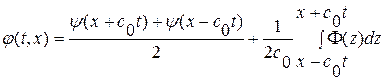 . (1. 58)
. (1. 58)
Тем самым доказано существование решения нашей задачи. Заметим теперь, что полученное решение совпадает с формулой Д' Аламбера. Отсюда следует теорема единственности для нашей задачи. С помощью прямой подстановки нетрудно убедиться, что функции типа 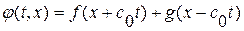 , где
, где  и
и 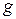 - кусочно-гладкие функции, удовлетворяют уравнению (1. 56), что также доказывает существование решения.
- кусочно-гладкие функции, удовлетворяют уравнению (1. 56), что также доказывает существование решения.
Сформулируем интегральный аналог первой краевой задачи для волнового уравнения на полуограниченной прямой 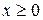 :
:
Найти функцию 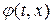 , определенную и кусочно-гладкую в области
, определенную и кусочно-гладкую в области 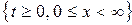 , удовлетворяющую интегральному уравнению
, удовлетворяющую интегральному уравнению
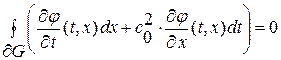 (1. 56)
(1. 56)
начальным условиям 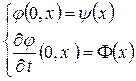 , где функции
, где функции 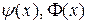 - кусочно-непрерывны.
- кусочно-непрерывны.
и граничному условию 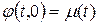 , где
, где  .
.
Контур  - произвольный кусочно-гладкий контур, лежащий в области
- произвольный кусочно-гладкий контур, лежащий в области  .
.
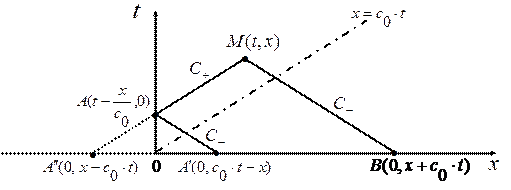
Рис. 2. 4
Решение: Будем искать решение  уравнения (1. 56) в некоторой точке М
уравнения (1. 56) в некоторой точке М  длязначений
длязначений 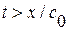 . Т. к. в области
. Т. к. в области 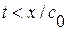 (т. е. под характеристикой
(т. е. под характеристикой 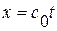 ) влияние граничного условия не сказывается и, след., решение определяется формулой (1. 58) как и в задаче Коши. Применим формулу (1. 56) к четырехугольнику
) влияние граничного условия не сказывается и, след., решение определяется формулой (1. 58) как и в задаче Коши. Применим формулу (1. 56) к четырехугольнику 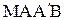 , образованному из 3-х отрезков характеристик и части оси
, образованному из 3-х отрезков характеристик и части оси  (Рис. 2. 4). Выполнив интегрирование вдоль отрезков характеристик
(Рис. 2. 4). Выполнив интегрирование вдоль отрезков характеристик 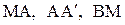 , получим:
, получим:
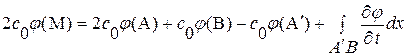 ,
,
подставив в полученную формулу координаты точек 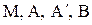 , найдем:
, найдем:
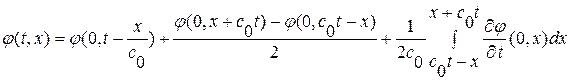 ,
,
или, подставляя заданные начальные и граничные условия, найдем окончательный вид искомого решения
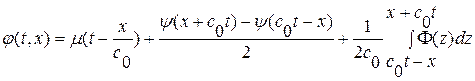 , при
, при 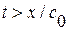 (1. 57)
(1. 57)
Из (1. 57) непосредственно следует единственность решения рассматриваемой задачи.
Аналогично может быть получено решение второй и третьей краевых задач.
Характеристики – линии распространения разрывов производных решений интегрального аналога (1. 56) волнового уравнения (линии слабого разрыва).
|
|
|
Покажем теперь, что для уравнения (1. 56) линиями разрыва производных функции 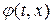 , получивших название линий слабого разрыва, могут быть только линии семейств характеристик
, получивших название линий слабого разрыва, могут быть только линии семейств характеристик 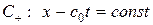 и
и 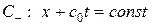 .
.
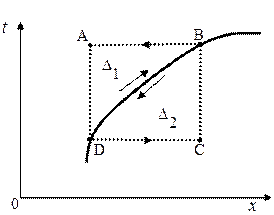 Док-во. Рассмотрим произвольную дифференцируемую кривую
Док-во. Рассмотрим произвольную дифференцируемую кривую  в фазовой плоскости и предположим, что эта линия является линией разрыва непрерывной, кусочно-дифференцируемой функции
в фазовой плоскости и предположим, что эта линия является линией разрыва непрерывной, кусочно-дифференцируемой функции 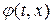 . Предположим для определенности, что
. Предположим для определенности, что  - возрастающая функция (Рис. 2. 5).
- возрастающая функция (Рис. 2. 5).
 | ||||
 | ||||
 | ||||
Рис. 2. 5
Теперь применим формулу (1. 56) последовательно - к прямоугольнику BADC,
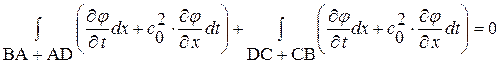 (1. 58)
(1. 58)
а также к криволинейным треугольникам 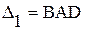 и
и 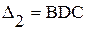 :
:
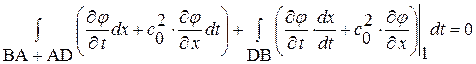 , (1. 59)
, (1. 59)
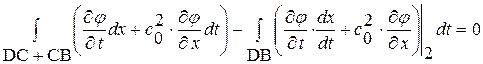 , (1. 60)
, (1. 60)
где символьное обозначение 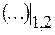 показывает, что выражения внутри скобок берутся как предельные значения на линии DB изнутри треугольников
показывает, что выражения внутри скобок берутся как предельные значения на линии DB изнутри треугольников 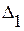 или
или 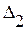 . Вычитая из суммы равенств (1. 59)+(1. 60) равенство (1. 58), получим:
. Вычитая из суммы равенств (1. 59)+(1. 60) равенство (1. 58), получим:
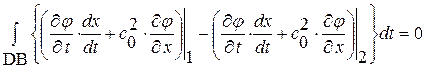 или, в силу произвольной малости дуги DB, найдем:
или, в силу произвольной малости дуги DB, найдем:
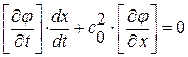 , (1. 61)
, (1. 61)
| |
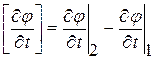 .
.
Равенства типа (1. 61) получили название динамических условий на кривой  слабого разрыва.
слабого разрыва.
Вычислим производную по времени от величины 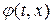 вдоль линии разрыва производных:
вдоль линии разрыва производных: 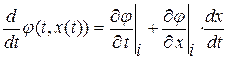 , где
, где 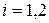 , причем в качестве значений производных можно брать предельные значения как со стороны
, причем в качестве значений производных можно брать предельные значения как со стороны 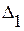 , так и
, так и 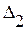 . Разность правых частей при
. Разность правых частей при 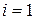 и
и 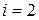 в виду непрерывности
в виду непрерывности 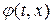 на кривой
на кривой  дает:
дает:
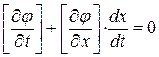 (1. 62)
(1. 62)
Равенства типа (1. 62) получили название кинематических условий на кривой  слабого разрыва.
слабого разрыва.
Рассмотрим теперь уравнения (1. 61) и (1. 62) как систему двух уравнений относительно двух неизвестных величин 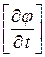 и
и 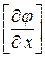 :
:
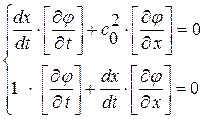 (1. 63)
(1. 63)
Как видно из этой однородной системы уравнений (1. 63), существование ненулевого решения (ненулевого значения по крайней мере одного из разрывов 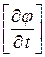 ,
, 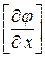 ) возможно только в случае, если главный определитель системы равен нулю, т. е.
) возможно только в случае, если главный определитель системы равен нулю, т. е.
если 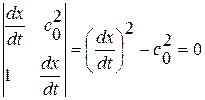 или, интегрируя,
или, интегрируя, 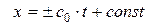 .
.
Таким образом, линии разрыва производных решения уравнения (1. 56) - линии слабого разрыва, являются характеристиками, что и требовалось доказать. Очевидно, что характеристики также могут являться и линиями гладкости решения уравнения (1. 56).
Проведенной вывод позволяет сформулировать еще одно определение характеристик – как линий в фазовой плоскости при постановке начальных условий на которых задача Коши для уравнения (1. 56) имеет неединственное решение. Действительно, мы показали, что при переходе через характеристику производные 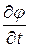 ,
, 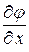 могут терпеть разрыв и, в частности, отличаться от значений на характеристике, следовательно, решение вне характеристики определяемое в ее малой окрестности как сумма
могут терпеть разрыв и, в частности, отличаться от значений на характеристике, следовательно, решение вне характеристики определяемое в ее малой окрестности как сумма 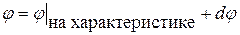 , где
, где 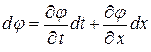 может быть найдено (продолжено в область вне характеристики) неоднозначно.
может быть найдено (продолжено в область вне характеристики) неоднозначно.
|
|
|
Математическое доказательство этого определения характеристик получим чуть позже в дифференциальной форме, путем перехода от одного волнового уравнения с одной искомой функцией  к эквивалентной ему линейной системе двух уравнений в частных производных первого порядка относительно двух искомых функций
к эквивалентной ему линейной системе двух уравнений в частных производных первого порядка относительно двух искомых функций 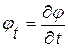 ,
, 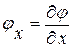 , т. е. к исходной линеаризованной системе уравнений (1. 26).
, т. е. к исходной линеаризованной системе уравнений (1. 26).
Сейчас же покажем, что характеристики семейств  – это линии слабого разрыва искомых функций
– это линии слабого разрыва искомых функций 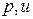 в фазовой плоскости
в фазовой плоскости  исходной линеаризованной системы уравнений квазиодномерной газовой динамики:
исходной линеаризованной системы уравнений квазиодномерной газовой динамики:
 , (1. 26. 1)
, (1. 26. 1)
 , (1. 26. 2)
, (1. 26. 2)
Доказательство: Рассмотрим произвольную дифференцируемую кривую  в фазовой плоскости и предположим, что при переходе через эту линию искомые функции
в фазовой плоскости и предположим, что при переходе через эту линию искомые функции 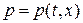 ,
, 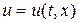 непрерывны, а частные производные от них (по крайней мере хотя бы одна) – разрывны. Примем также, что площадь
непрерывны, а частные производные от них (по крайней мере хотя бы одна) – разрывны. Примем также, что площадь 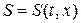 меняется гладким образом при переходе через линию
меняется гладким образом при переходе через линию  .
.
Отметим индексами 1 и 2 величины по разные стороны линии разрыва производных  . Тогда
. Тогда 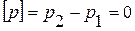 ,
, 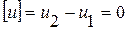 ,
, 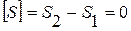 . Запишем систему уравнений (1. 26. 1-2) для точек, стремящихся к точке
. Запишем систему уравнений (1. 26. 1-2) для точек, стремящихся к точке  кривой
кривой  со стороны 1 и со стороны 2. В переделе имеем
со стороны 1 и со стороны 2. В переделе имеем
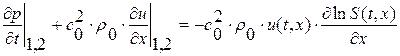 ,
,
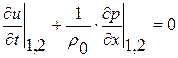 ,
,
Как видим, правая часть в первом уравнении одинакова как для системы уравнений с индексом 1, так и для системы с индексом 2. Вычитая из системы с индексом 2 систему уравнений с индексом 1 получаем динамические условия на кривой слабого разрыва  :
:
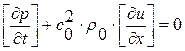 , (Д. У. 1)
, (Д. У. 1)
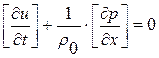 , (Д. У. 2)
, (Д. У. 2)
где, как и прежде, скачок  и т. д.
и т. д.
Получим теперь систему кинематических условий на кривой  слабого разрыва.
слабого разрыва.
Для этого вычислим производную по времени от величин 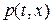 и
и  вдоль линии разрыва производных: например,
вдоль линии разрыва производных: например, 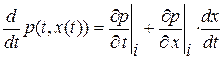 , где
, где 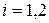 , причем в качестве значений производных можно брать предельные значения как со стороны кривой с индексом 1, так и 2. Разность правых частей при
, причем в качестве значений производных можно брать предельные значения как со стороны кривой с индексом 1, так и 2. Разность правых частей при 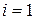 и
и 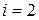 в виду непрерывности функций
в виду непрерывности функций 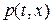 и
и  на кривой
на кривой  дает:
дает:
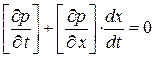 (К. У. 1)
(К. У. 1)
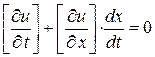 (К. У. 2)
(К. У. 2)
Рассмотрим теперь уравнения (Д. У. 1), (Д. У. 2), (К. У. 1), (К. У. 2) как систему четырех уравнений относительно четырех неизвестных величин 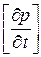 ,
, 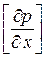 ,
, 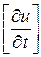 ,
, 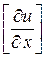 :
:
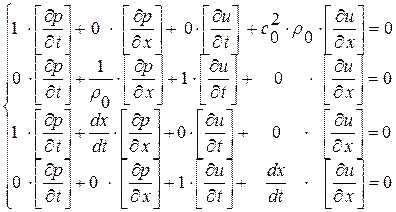
Для существования ненулевого решения данной линейной однородной алгебраической системы уравнений необходимо, чтобы главный определитель системы 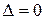 . Вычислим его:
. Вычислим его:
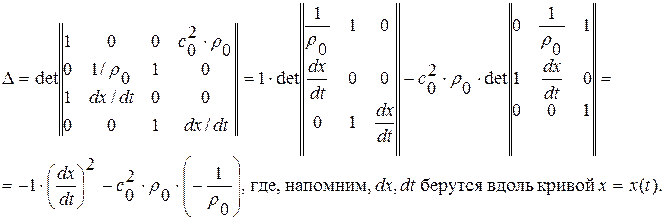
Из условия 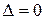 получим
получим 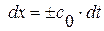 , что и требовалось доказать.
, что и требовалось доказать.
Докажем еще одно удивительное свойство характеристик семейств  : Для линеаризованной системы уравнений квазиодномерной (
: Для линеаризованной системы уравнений квазиодномерной (  ) газовой динамики сильные разрывы искомых функций
) газовой динамики сильные разрывы искомых функций 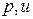 распространяются только по характеристикам.
распространяются только по характеристикам.
Док-во. Напомним, что случай 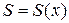 описывает распространение возмущений с плоской (
описывает распространение возмущений с плоской ( 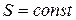 ), цилиндрической (
), цилиндрической ( 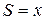 ) и сферической (
) и сферической ( 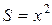 ) симметрией. Запишем исходную линеаризованною систему уравнений (1. 26. 1-2) в следующем виде:
) симметрией. Запишем исходную линеаризованною систему уравнений (1. 26. 1-2) в следующем виде:
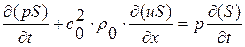 , (1. 26. 1)’
, (1. 26. 1)’
 , (1. 26. 2)’
, (1. 26. 2)’
Перейдем к интегральной форме записи уравнений (1. 26. 1)’, (1. 26. 2)’. Для этого проинтегрируем уравнения (1. 26. 1)’, (1. 26. 2)’ по односвязной области  с границей
с границей  - непрерывной кусочно-гладкой функцией и воспользуемся формулой Грина:
- непрерывной кусочно-гладкой функцией и воспользуемся формулой Грина:
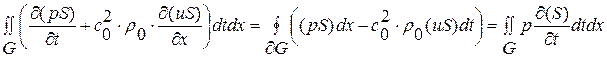 ,
,
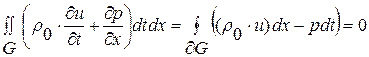
Получим интегральный аналог исходной линейной системы уравнений (1. 26) квазиодномерной газовой динамики для случая  :
:
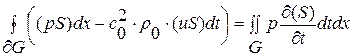 (1. 26. 1)-И
(1. 26. 1)-И
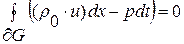 (1. 26. 2)-И
(1. 26. 2)-И
Р-м произвольную дифференцируемую кривую  в фазовой плоскости
в фазовой плоскости  и предположим, что эта линия является линией разрыва искомых функций
и предположим, что эта линия является линией разрыва искомых функций  и
и  . Примем также, что
. Примем также, что  - непрерывная функция. Пусть
- непрерывная функция. Пусть  - возрастающая функция (Рис. 2. 5).
- возрастающая функция (Рис. 2. 5).
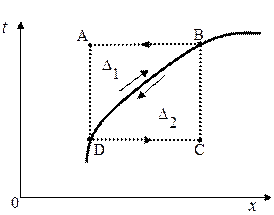 | |||
 | |||
Рис. 2. 5
Теперь применим формулы (1. 26. 1)-И и (1. 26. 2)-И последовательно - к прямоугольнику BADC, а также к криволинейным треугольникам 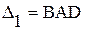 и
и 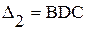 . Вычитая из суммы равенств, полученных для треугольников
. Вычитая из суммы равенств, полученных для треугольников 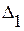 и
и 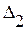 , равенство для прямоугольни-ка BADC и, учитывая, что
, равенство для прямоугольни-ка BADC и, учитывая, что 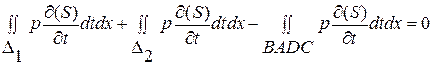 , получим два следствия из исходных уравнений (1. 26. 1)-И, (1. 26. 2)-И:
, получим два следствия из исходных уравнений (1. 26. 1)-И, (1. 26. 2)-И:
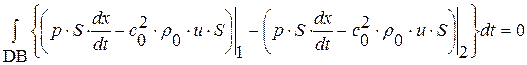 ,
,
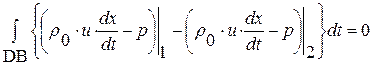 ,
,
далее, в силу произвольной малости дуги DB, получим:
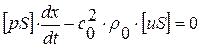 или, т. к. скачок
или, т. к. скачок 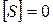 ,
, 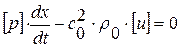
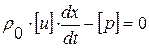 . Рассмотрим теперь полученные соотношения как систему 2-х линейных однородных алгебраических уравнений относительно 2-х неизвестных
. Рассмотрим теперь полученные соотношения как систему 2-х линейных однородных алгебраических уравнений относительно 2-х неизвестных 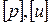 :
: 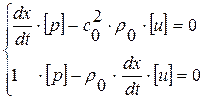 (С/Р)
(С/Р)
Для существования ненулевого решения системы необходимо, чтобы главный определитель системы 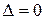 , т. е.
, т. е. 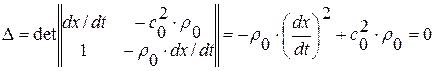 , следовательно,
, следовательно, 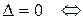
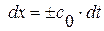 , т. е. линия
, т. е. линия  является характеристикой.
является характеристикой.
Т. о., если у решений линеаризованной системы уравнений квазиодномерной (  ) газовой динамики имеют место быть сильные разрывы, то они распространяются только по характеристикам семейств
) газовой динамики имеют место быть сильные разрывы, то они распространяются только по характеристикам семейств  .
.
Подведем некоторые итоги:
- У линеаризованной системы уравнений квазиодномерной (
 ) газовой динамики (1. 26. 1-2) имеется два семейства характеристик
) газовой динамики (1. 26. 1-2) имеется два семейства характеристик 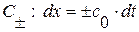 .
. - Эти и только эти характеристики семейств
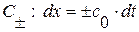 могут быть:
могут быть:
а). линиями гладкости решения, если решение гладкое,
б). линиями слабого разрыва, если решение – непрерывно, а производные – разрывны. При этом скачки производных связаны между собой системой кинематических (К. У. 1-2) и динамических (Д. У. 1-2) соотношений на слаб. разрыве,
в). линиями сильного разрыва (разрыва первого рода), если решение – разрывно. При этом скачки искомых функций 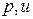 связаны соотношением (С/Р) на сильном разрыве:
связаны соотношением (С/Р) на сильном разрыве: 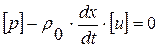 .
.
Перейдем теперь к доказательству того факта, что характеристики семейств  – это линии в фазовой плоскости
– это линии в фазовой плоскости  , при постановке начальных условий на которых задача Коши как для волнового уравнения (1. 29. 2), так и для системы уравнений (1. 26. 1-2) имеет неединственное решение.
, при постановке начальных условий на которых задача Коши как для волнового уравнения (1. 29. 2), так и для системы уравнений (1. 26. 1-2) имеет неединственное решение.
Для этого перейдем от одного волнового уравнения с одной искомой функцией  к эквивалентной ему линейной системе двух уравнений в частных производных первого порядка относительно двух искомых функций
к эквивалентной ему линейной системе двух уравнений в частных производных первого порядка относительно двух искомых функций 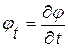 ,
, 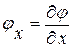 . Далее для компактности примем обозначения, что
. Далее для компактности примем обозначения, что 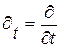 и
и 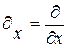 . Тогда указанная система примет вид:
. Тогда указанная система примет вид:
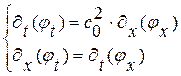 (1. 64)
(1. 64)
первое уравнение в (1. 64)– прямое следствие исходного волнового уравнения, второе уравнение – условие равенства смешанных производных – необходимо для того, чтобы указать, что новые искомые функции 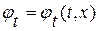 ,
, 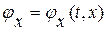 - суть частные производные по разным аргументам одной и той же исходной функции
- суть частные производные по разным аргументам одной и той же исходной функции  .
.
Заметим, что система (1. 64) – это равносильная форма записи исходной линеаризованной системы (1. 26. 1-2), записанной с учетом формул (1. 29. 1) для случая 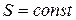 в терминах производных от потенциала
в терминах производных от потенциала  . Поэтому все рассуждения, в которых участвуют
. Поэтому все рассуждения, в которых участвуют 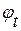 ,
, 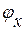 , фактически являются рассуждениями относительно величин давления (возмущения)
, фактически являются рассуждениями относительно величин давления (возмущения) 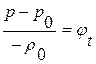 и скорости (возмущения)
и скорости (возмущения) 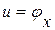 .
.
Вначале поставим задачу нахождения непрерывно дифференцируемого решения 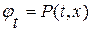 ,
, 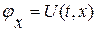 системы (1. 64) в окрестности произвольной дифференцируемой кривой
системы (1. 64) в окрестности произвольной дифференцируемой кривой  , на которой заданы значения функций
, на которой заданы значения функций 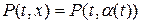 ,
, 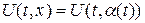 (т. е. поставим задачу Коши для системы (1. 64) на произвольной кривой
(т. е. поставим задачу Коши для системы (1. 64) на произвольной кривой  ). Задание начальных значений искомых функций на кривой
). Задание начальных значений искомых функций на кривой  позволяет вычислить значение производной от искомых решений вдоль кривой, но этого недостаточно для того, чтобы определить решение в окрестности кривой. Действительно, решение в точке расположенной вблизи нашей кривой может быть вычислено как сумма значений решения на кривой
позволяет вычислить значение производной от искомых решений вдоль кривой, но этого недостаточно для того, чтобы определить решение в окрестности кривой. Действительно, решение в точке расположенной вблизи нашей кривой может быть вычислено как сумма значений решения на кривой 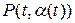 или
или 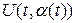 плюс приращение
плюс приращение 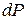 или
или 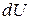 , где
, где 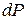 и
и 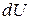 определяются из соотношений (1. 65) по известным значениям приращений координат
определяются из соотношений (1. 65) по известным значениям приращений координат 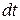 или
или 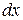 из точки кривой
из точки кривой 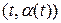 до выбранной точки вне кривой
до выбранной точки вне кривой 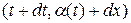 и значениям частных производных
и значениям частных производных 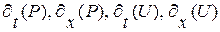 в точке кривой
в точке кривой 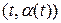 .
.
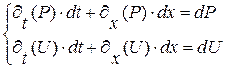 (1. 65)
(1. 65)
Рассматривая теперь систему (1. 65), как систему уравнений для определения 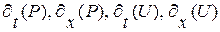 на кривой
на кривой  (т. е. когда: 1). известны
(т. е. когда: 1). известны 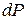 ,
, 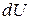 , 2).
, 2). 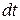 и
и 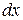 связаны между собой требованием
связаны между собой требованием 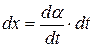 ) мы вынуждены признать, что двух уравнений (1. 65) недостаточно для вычисления 4-х производных. И здесь нам на помощь приходит система (1. 64) если принять, что она выполняется не только для точек вне кривой
) мы вынуждены признать, что двух уравнений (1. 65) недостаточно для вычисления 4-х производных. И здесь нам на помощь приходит система (1. 64) если принять, что она выполняется не только для точек вне кривой  , но и для точек, принадлежащих этой кривой.
, но и для точек, принадлежащих этой кривой.
Выпишем эту линейную, неоднородную алгебраическую систему 4-х уравнений (1. 64), (1. 65) относительно 4-х неизвестных 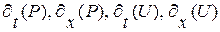 , выполненную для каждой точки
, выполненную для каждой точки  кривой
кривой  . Для удобства дальнейших выкладок выпишем в каждом из уравнений этой системы все неизвестные даже если они имеют нулевые коэффициенты:
. Для удобства дальнейших выкладок выпишем в каждом из уравнений этой системы все неизвестные даже если они имеют нулевые коэффициенты:
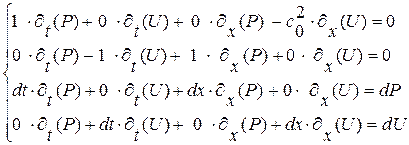 (1. 66)
(1. 66)
Для существования и единственности решения линейной алгебраической системы уравнений (1. 66) с неизвестными 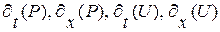 необходимо и достаточно, чтобы главный определитель системы
необходимо и достаточно, чтобы главный определитель системы 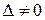 . Вычислим его:
. Вычислим его:
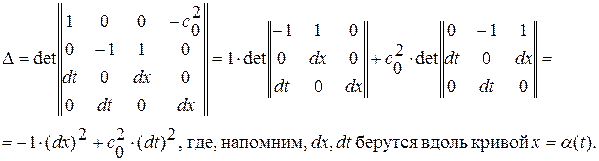
Условие 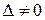 означает, что
означает, что 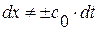 , т. е., что
, т. е., что 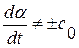 или, другими словами, что кривая
или, другими словами, что кривая  не является характеристикой.
не является характеристикой.
Итак, решение задачи нахождения непрерывно дифференцируемого решения 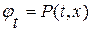 ,
, 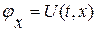 системы (1. 64) в окрестности произвольной дифференцируемой кривой
системы (1. 64) в окрестности произвольной дифференцируемой кривой  , на которой заданы значения функций
, на которой заданы значения функций 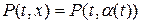 ,
, 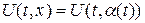 , существует и единственно, если кривая
, существует и единственно, если кривая  не является характеристикой.
не является характеристикой.
Возникает естественный вопрос: как быть, если все-таки кривая  является характеристикой? Ответ на этот вопрос отчасти был дан на
является характеристикой? Ответ на этот вопрос отчасти был дан на
|
|
|


