 |
Метод математической индукции
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
 |
ФГБОУ ВО
“Воронежский государственный УНИВЕРСИТЕТ
ИНЖЕНЕРНЫХ технологиЙ”
Кафедра информационных технологий,
Моделирования и управления
 |
МНОЖЕСТВА. ЭЛЕМЕНТЫ
КОМБИНАТОРНОГО АНАЛИЗА
Методические указания
К практическим занятиям
Для студентов, обучающихся по направлениям
09.03.02 – “Информационные системы и технологии”
09.03.03 – “Прикладная информатика”
Очной формы обучения
ВОРОНЕЖ
УДК 517.8; 519.1
Множества. Элемента комбинаторного анализа [Электронный ресурс]: метод. указания к практическим занятиям / Воронеж. гос. ун-т инж. технол.; сост. Ю. В. Бугаев, И. Ю. Шурупова,. – Воронеж: ВГУИТ, 2016. – 32 с. – [ЭИ]
Методические указания разработаны в соответствии с требованиями ФГОС ВО подготовки выпускников по направлениям 09.03.02 – “Информационные системы и технологии”, 09.03.03 – “Прикладная информатика”. Они предназначены для закрепления теоретических знаний дисциплин “Теоретические основы информационных технологий”, “Теоретическая информатика”.
Библиогр.: 5 назв.
Составители: профессор Ю.В. БУГАЕВ,
доцент И.Ю. ШУРУПОВА,
ассистент Д.А. ЛИТВИНОВ
Научный редактор доцент Л.А. КОРОБОВА
Рекомендуется к размещению
в ЭОС и ЭБ ВГУИТ
Ó Бугаев Ю.В., Шурупова И.Ю.,
Литвинов Д.А., 2016
Ó ФГБОУ ВО “Воронежский
государственный университет
инженерных технологий”, 2016
Оригинал-макет данного издания является собственностью Воронежского государственного университета инженерных технологий, его репродуцирование (воспроизведение) любым способом без согласия университета запрещается.
|
|
|
Метод математической индукции
Метод математической индукции – универсальный способ доказательства утверждений, зависящих от натурального аргумента n. Он основан на следующем принципе математической индукции: утверждение 
справедливо для любого натурального 
, если:
10 оно справедливо для n = n 0;
20 из того, что оно верно для всех n £ k (k ³ n 0) следует его справедливость для n = k + 1.
Этот принцип, являющийся одной из аксиом натурального ряда можно перефразировать так: если в цепочке утверждений первое утверждение 
верно, а из справедливости 
следует справедливость 
, то вся цепочка состоит из верных утверждений.
Задача 1. Найти сумму 
.
Решение. Имеем: 
; 
; 
; 
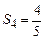. Есть подозрение, что 
. Докажем эту формулу.
10. При n 0 = 1 
– формула верна.
20. Предположим, что для произвольного k ³1 для всех n £ k . В частности, для n = k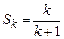 
. Найдем 
. Имеем 
. По предположению это равно
= 
= 
= 
,
что и требовалось доказать.
Однако индуктивное утверждение может быть неверным, простая индукция позволяет лишь выдвинуть гипотезу, которую надо доказать. Например, анализируя числа 1, 3, 5, 7 можно прийти к неверному заключению, что все нечетные числа являются простыми.
“Докажем”, что все натуральные числа равны между собой. Предположим, что k = k + 1. Прибавим по 1 к обеим частям этого равенства. Получим k + 1 = k + 2, что и требовалось доказать. Ошибка этого “доказательства” состоит в отсутствии проверки утверждения при n 0 = 1.
Задача 2. Доказать неравенство 2 n > 2 n + 1 при n ³ 3.
Решение.
10. При n 0 = 3 имеем 23 > 7 верное неравенство.
20. 2 k + 1= 2×2 k > 2(2 k + 1) = 4 k + 2 = (2 k + 3) + (2 k – 1) > 2 k + 3.
Задача 3. Доказать, что для любого n ³ 0 число 11 n +2 +122 n +1 делится на 133.
Решение.
10. 112 + 121 = 133 – верно при n = 0.
20. 11 k +3 + 122( k + 1) +1 = 11×11 k + 2 + 144×122 k + 1 = (144–133) ×11 k + 2 + +144×122 k + 1 = 144 × (11 k + 2 + 122 k + 1) – 133×11 k + 2.
|
|
|
В полученной разности уменьшаемое делится на 133 по предположению, а вычитаемое содержит множитель 133. Следовательно, все выражение делится на 133.
Контрольные вопросы и задания
1. Доказать формулу Sn = 12+22+32+…+ n 2 = n (n +1)(2 n +1)/6.
2. Обозначим Hn = 1 + 1/2 + 1/3 +…+ 1/ n – гармонические числа. Доказать, что Нn неограниченно сверху, т.е. что Нn ® +¥ (
).
3. Доказать, что любую сумму денег более 7 копеек можно уплатить монетами достоинством 3 и 5 копеек.
4. Найти формулы для вычисления:
а) 
б) 
Доказать формулы и утверждения (5 – 18).
5. 
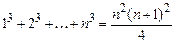
6. 
.
7. При любом х ¹ 1, 
.
8. Сумма кубов трех последовательных натуральных чисел n 3 + (n + 1)3 + (n + 2)3 делится на 9.
9. Выражение 
делится без остатка на 9.
10. Число диагоналей выпуклого n -угольника k = n (n –2) /2.
11. Последовательность аn = 
(n корней) возрастает.
12. cos a×cos 2a×… ×cos 2na =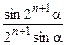 
.
13. 
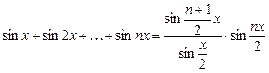
14. 
.
15. 
.
16. 
17. 
18. 
|
|
|
