 |
Длинная линия с потерями. Телеграфные уравнения.
|
|
|
|
Рассмотрим отрезок dx длинной линии с потерями, представленный на рис. 3.26, погонными параметрами которой являются  .
.

Рис.3.26. Отрезок длинной линии с потерями.
Приращения напряжения и тока на отрезке линии dx можно представить следующими дифференциальными уравнениями:
 , (3.147)
, (3.147)
 . (3.148)
. (3.148)
Разделив оба уравнения на 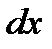 , получим
, получим
 , (3.149)
, (3.149)
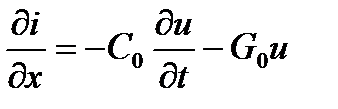 . (3.150)
. (3.150)
Дифференцируя уравнение (3.149) по x, а уравнение (3.150) по t, получим:
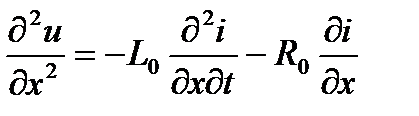 , (3.151)
, (3.151)
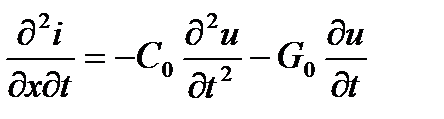 . (3.152)
. (3.152)
Подставив (3.150) и (3.152) в (3.151), получим дифференциальное уравнение второго порядка, называемое телеграфным уравнением для напряжения:
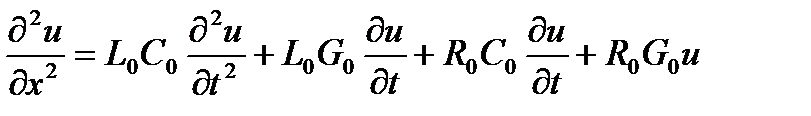 . (3.153)
. (3.153)
Это уравнение упрощается, если для его коэффициентов выполняется следующее условие, называемое условием Хевисайда:
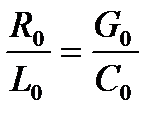 . (3.154)
. (3.154)
Это условие можно записать в другом виде:
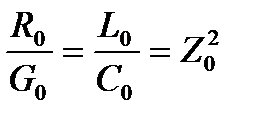 . (3.155)
. (3.155)
Отсюда следует:
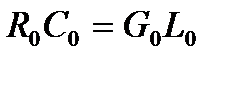 . (3.156)
. (3.156)
Подставив (3.156) в телеграфное уравнение (3.153), получим:
 . (3.157)
. (3.157)
Разделив (3.157) на  , получим:
, получим:
 , (3.158)
, (3.158)
где: 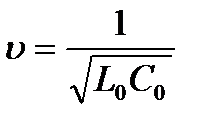 - скорость распространения волны в линии.
- скорость распространения волны в линии.
Обозначив 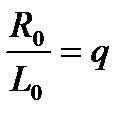 , получим:
, получим:
 . (3.159)
. (3.159)
Введем новую переменную u 0, положив  . Найдём производные:
. Найдём производные:


Подставив производные в (3.159), получим следующее уравнение для напряжения:
 . (3.160)
. (3.160)
Аналогичное уравнение может быть получено для тока.
Таким образом, при выполнении условия Хевисайда телеграфное уравнение приводится к волновому. Это означает, что в линии с потерями может распространяться волна любой формы без искажений. Отличие решения этого уравнения по сравнению с уравнениями для линии без потерь заключается в наличии множителя 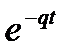 , с которым связаны u и u 0, что означает затухание прямой и обратной волны. При выполнении условий Хевисайда затухание на высоких частотах минимально и равно затуханию на низких частотах. При несоблюдении условий Хевисайда передаваемые колебания сложной формы искажаются вследствие неодинакового затухания для разных частот и зависимости скорости распространения от частоты.
, с которым связаны u и u 0, что означает затухание прямой и обратной волны. При выполнении условий Хевисайда затухание на высоких частотах минимально и равно затуханию на низких частотах. При несоблюдении условий Хевисайда передаваемые колебания сложной формы искажаются вследствие неодинакового затухания для разных частот и зависимости скорости распространения от частоты.
|
|
|
30
Прямоугольный волновод
Прямоугольный волновод является длинной линией в диапазоне сверхвысоких частот. Прямоугольный волновод представляет собой полую трубу из проводящего материала, служащую для передачи энергии электромагнитной волны, распространяющейся внутри волновода. Если электрический и магнитный векторы 

 и
и 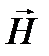 лежат в плоскости, нормальной к направлению линии, то имеется поток энергии, направленный вдоль линии, выражаемый вектором Пойнтинга:
лежат в плоскости, нормальной к направлению линии, то имеется поток энергии, направленный вдоль линии, выражаемый вектором Пойнтинга:
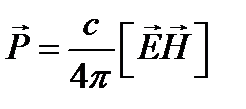 . (3.196)
. (3.196)
В основе теории волноводов лежат уравнения Максвелла. Для случая, когда диэлектрическая проницаемость ε=1, магнитная проницаемость μ=1 и проводимость σ=0 (это справедливо для воздуха и вакуума), можно записать уравнения Максвелла в векторной форме:
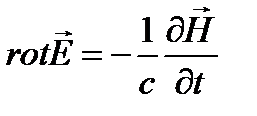 , (3.197)
, (3.197)
 , (3.198)
, (3.198)
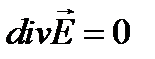 , (3.199)
, (3.199)
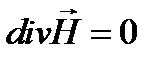 , (3.200)
, (3.200)
где c – скорость света в вакууме.
Для установившегося синусоидального режима:
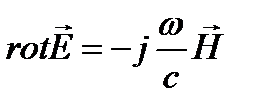 , (3.201)
, (3.201)
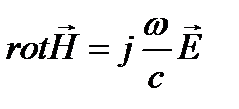 . (3.202)
. (3.202)
Найдем  из уравнения (3.201):
из уравнения (3.201):
 , (3.203)
, (3.203)
где  - волновое число.
- волновое число.
Подставим значение 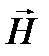 в уравнение (3.202):
в уравнение (3.202):

 . (3.204)
. (3.204)
Учитывая, что
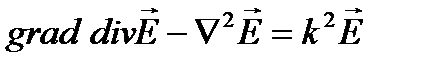 (3.205)
(3.205)
и
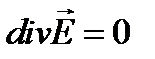 , (3.206)
, (3.206)
получим:
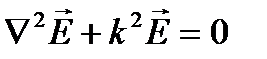 . (3.207)
. (3.207)
Аналогичное уравнение можно получить и для вектора напряженности магнитного поля:
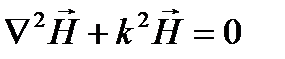 . (3.208)
. (3.208)
Уравнения (3.207) и (3.208) - это векторная форма волновых уравнений.
Для перехода от векторной формы уравнений к скалярной выберем прямоугольную систему координат:  Будем рассматривать проекции электрического вектора
Будем рассматривать проекции электрического вектора 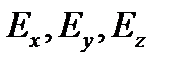 на координатные оси. Каждая составляющая поля зависит от координат и от времени. Закон изменения каждой составляющей от времени выражается множителем
на координатные оси. Каждая составляющая поля зависит от координат и от времени. Закон изменения каждой составляющей от времени выражается множителем 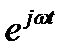 . Опустив этот множитель, мы придадим величинам
. Опустив этот множитель, мы придадим величинам 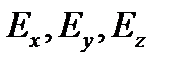 смысл комплексных амплитуд составляющих электрического поля.
смысл комплексных амплитуд составляющих электрического поля.
Запишем уравнение (2.206) в виде трех уравнений для составляющих поля:
|
|
|
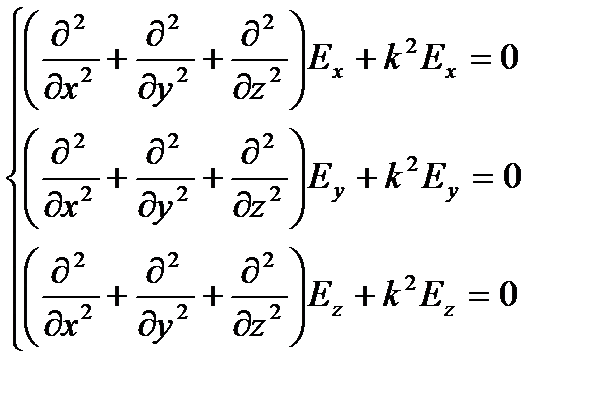 (3.209)
(3.209)
Решением этих уравнений являются функции трёх переменных 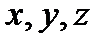 . Будем искать решение в виде произведения трёх функций, каждая из которых зависит только от одного аргумента:
. Будем искать решение в виде произведения трёх функций, каждая из которых зависит только от одного аргумента:
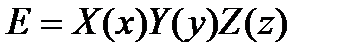 . (3.210)
. (3.210)
Это решение подставляется в уравнения (3.209) и эти уравнения интегрируются. В интегралы вводятся граничные условия.
Для выяснения граничных условий будем считать, что стенки волновода идеально проводят. Поэтому касательная составляющая вектора  около самой стенки равна 0. То есть вектор
около самой стенки равна 0. То есть вектор  должен быть нормален к стенке волновода на ее поверхности. Будем рассматривать волновод прямоугольного сечения.
должен быть нормален к стенке волновода на ее поверхности. Будем рассматривать волновод прямоугольного сечения.

Рис.3.31. к определению граничных условий
Граничные условия запишутся следующим образом:
 =0 при
=0 при  , (3.211)
, (3.211)
 =0 при
=0 при  , (3.212)
, (3.212)
 =0 при
=0 при 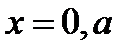 и
и  . (3.213)
. (3.213)
Считаем, что волновод бесконечно длинный вдоль оси  . При некоторых условиях вдоль оси
. При некоторых условиях вдоль оси  может распространяться бегущая волна, которая выражается функцией
может распространяться бегущая волна, которая выражается функцией
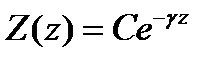 , (3.214)
, (3.214)
где 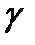 - постоянная распространения.
- постоянная распространения.
Функции 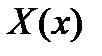 и
и 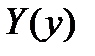 представляют зависимость амплитуды от координат точки в сечении волновода. Эти функции представляют собой волны, распространяющиеся поперек волновода, т.е. перпендикулярно к стенкам. Так как стенки бесконечно проводящие, то в направлении осей
представляют зависимость амплитуды от координат точки в сечении волновода. Эти функции представляют собой волны, распространяющиеся поперек волновода, т.е. перпендикулярно к стенкам. Так как стенки бесконечно проводящие, то в направлении осей 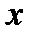 и
и  могут существовать только стоячие волны. Для касательных составляющих на стенках получаются узлы, для нормальных – пучности. Исходя из этих представлений, можно записать для уравнений (3.209) решения вида (3.210), удовлетворяющие граничным условиям:
могут существовать только стоячие волны. Для касательных составляющих на стенках получаются узлы, для нормальных – пучности. Исходя из этих представлений, можно записать для уравнений (3.209) решения вида (3.210), удовлетворяющие граничным условиям:
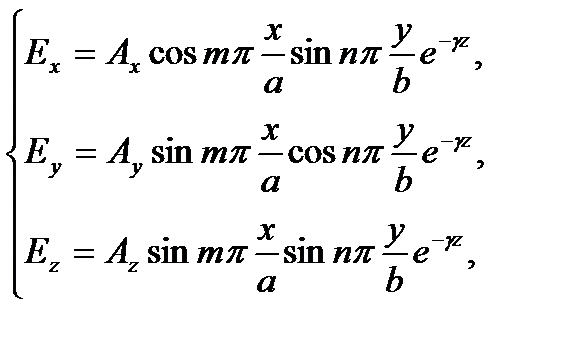 (3.215)
(3.215)
где:
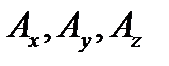 - постоянные, зависящие от условий возбуждения волновода;
- постоянные, зависящие от условий возбуждения волновода;
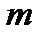 и
и  – любые положительные целые числа.
– любые положительные целые числа.
Найдём вторые производные  :
:
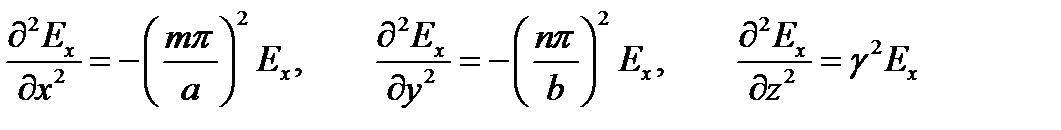 .
.
Подставим производные в первое уравнение (3.209):
 . (3.216)
. (3.216)
Электромагнитная волна в волноводе будет распространяться без затуханий, если постоянная распространения будет мнимой. А это будет при условии:
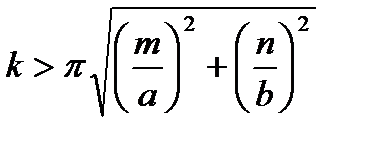 (3.217)
(3.217)
или
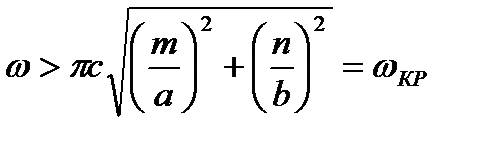 , (3.218)
, (3.218)
где 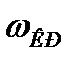 - критическая частота.
- критическая частота.
При этом
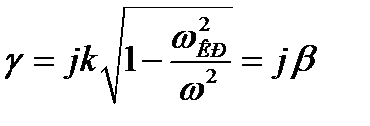 . (3.219)
. (3.219)
При 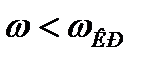 постоянная распространения
постоянная распространения 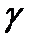 вещественна и волна будет затухать.
вещественна и волна будет затухать.
Итак, волновод обладает свойствами фильтра верхних частот: в нём распространяются без затухания волны с частотой выше некоторой граничной частоты  . Граничная частота
. Граничная частота  тем выше, чем меньше размеры волновода. В полосе прозрачности, т.е. при
тем выше, чем меньше размеры волновода. В полосе прозрачности, т.е. при  , постоянная распространения
, постоянная распространения  является мнимой величиной. Это значит, что вектор
является мнимой величиной. Это значит, что вектор  , не изменяя своей величины при распространении волны вдоль волновода, изменяется по фазе. Фазовый сдвиг равен
, не изменяя своей величины при распространении волны вдоль волновода, изменяется по фазе. Фазовый сдвиг равен
|
|
|
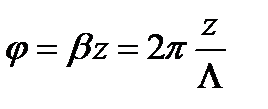 , (3.220)
, (3.220)
где 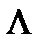 - длина волны в волноводе.
- длина волны в волноводе.
Из предыдущего выражения следует, что
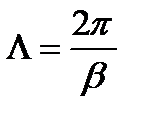 . (3.221)
. (3.221)
Подставляя значение 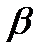 , получаем
, получаем
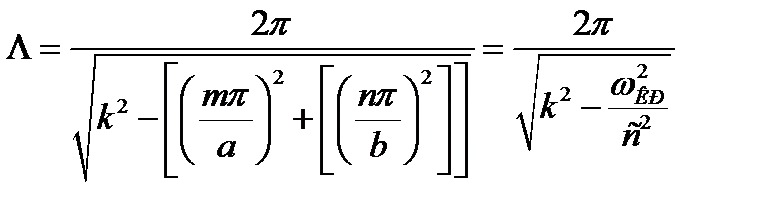 . (3.222)
. (3.222)
Так как 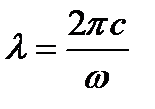 ,
,
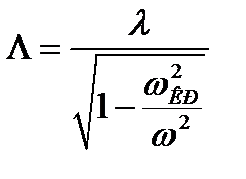 . (3.223)
. (3.223)
Поскольку длина волны пропорциональна скорости распространения, то
 . (3.224)
. (3.224)
Отсюда скорость распространения волны в волноводе:
 . (3.225)
. (3.225)
Из этого выражения видно, что скорость распространения волны в волноводе всегда больше скорости света в открытом пространстве. Имеется ввиду фазовая скорость, то есть скорость перемещения в пространстве точек, в которых наблюдается определенная фаза колебаний, например максимум или ноль. Групповая скорость или скорость распространения энергии волны ни при каких обстоятельствах не может превзойти скорость света. Скорость распространения становится равной бесконечности при 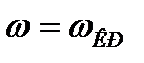 . Скорость распространения становится мнимой при
. Скорость распространения становится мнимой при 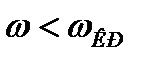 . Это означает, что на частотах ниже критической частоты в волноводе имеется быстро затухающее по длине волновода колебание вектора
. Это означает, что на частотах ниже критической частоты в волноводе имеется быстро затухающее по длине волновода колебание вектора 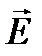 . Зависимость фазовой скорости от частоты в физике называется дисперсией.
. Зависимость фазовой скорости от частоты в физике называется дисперсией.
Критическая длина волны в волноводе равна:
 . (3.226)
. (3.226)
Граничная длина волны имеет порядок периметра сечения волновода. Поэтому волноводы приемлемых размеров могут применяться лишь при очень высоких частотах. Наиболее широкое применение получили волноводы с длиной волны 3 см и 10 см. Волноводы являются составной частью аппаратуры СВЧ.
31
|
|
|


