 |
Ускорение точки. Угловое ускорение тела
|
|
|
|
Метод полюса. Дифференцируя (14.1) по времени, получим
 ,
,
то есть вектор ускорения любой точки тела при плоском движении равен геометрической сумме векторов ускорения полюса и ее ускорения во вращении вокруг этого полюса (рис. 14.11).

|
| A |
| B |

|

|

|

|
| Рис. 14.11 |

|
 ,
,
где  (
( - угловое ускорение тела),
- угловое ускорение тела),  .
.
Модуль относительного ускорения
 .
.
Тогда
 .
.
Полное ускорение  составляет с прямой
составляет с прямой  угол
угол  , не зависящий от выбора полюса:
, не зависящий от выбора полюса:  .
.
Билет№5 Начало в билете№8
В каждый момент времени при движении плоской фигуры в своей плоскости, если угловая скорость и угловое ускорение не равны нулю одновременно ( ), имеется единственная точка
), имеется единственная точка  этой фигуры, ускорение которой в данный момент времени равно нулю (рис. 14.12). Эта точка называется мгновенным центром ускорений (МЦУ).
этой фигуры, ускорение которой в данный момент времени равно нулю (рис. 14.12). Эта точка называется мгновенным центром ускорений (МЦУ).
| Q |
| A |
| B |
| C |
| μ |
| μ |
| μ |

|

|

|
| Рис. 14.13 |
| ε |
| ω |

|
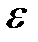
|

|
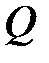
|
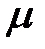
|

|

|
| Рис. 14.12 |
| O |
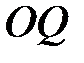 , полученном поворотом вектора
, полученном поворотом вектора  на угол
на угол 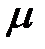 в направлении
в направлении 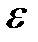 . Только в этом случае векторы
. Только в этом случае векторы 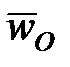 и
и 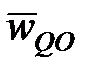 могут иметь одинаковые модули и быть противоположно направлены, то есть
могут иметь одинаковые модули и быть противоположно направлены, то есть
 , или
, или  ,
,
где  .
.
Следовательно,
 .
.
Из приведенных рассуждений следует, что МЦУ является единственной точкой, имеющей ускорение, равное нулю. В общем случае МЦУ изменяет свое положение с течением времени.
Выбрав точку 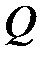 за полюс (рис. 14.13), имеем
за полюс (рис. 14.13), имеем
 , так как
, так как  .
.
Следовательно,  ,
,
как и для других точек, например:
 .
.
Ускорения точек прямо пропорциональны их расстояниям до МЦУ:
 .
.
Ускорения точек тела при плоском движении можно определить так же, как при его вращательном движении вокруг МЦУ с угловой скоростью  и угловым ускорением
и угловым ускорением  .
.
|
|
|
В общем случае МЦС и МЦУ не совпадают, являясь разными точками подвижной плоскости.

| Рис. 14.14 |
|

|
|
1.  (рис. 14.14).
(рис. 14.14).
Угол 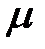 равен нулю:
равен нулю:  .
.

| Рис. 14.15 |
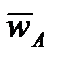
|

|

|
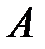 расстояние
расстояние 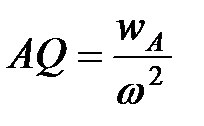 . Векторы ускорений точек направлены к мгновенному центру ускорений
. Векторы ускорений точек направлены к мгновенному центру ускорений 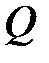 .
.
2.  (рис. 14.15).
(рис. 14.15).
Угол  равен
равен  :
:  . При известном ускорении точки
. При известном ускорении точки  расстояние
расстояние  .
.
| Q |
| A |
| B |
| μ |
| μ |
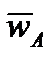
|
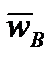
|
| ε |
| Рис. 14.16 |
3.  (рис. 14.16).
(рис. 14.16).
Находим угол 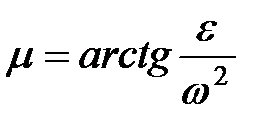 . В сторону вращения
. В сторону вращения  поворачиваем на угол
поворачиваем на угол  известный вектор
известный вектор  и на полученном луче откладываем отрезок
и на полученном луче откладываем отрезок  .
.
Векторы ускорений всех точек тела направлены под углом  к отрезкам, соединяющим точки с мгновенным центром ускорений.
к отрезкам, соединяющим точки с мгновенным центром ускорений.
Билет№4
Вращением твердого тела вокруг неподвижной точки, или сферическим движением твердого тела, называется такое движение, при котором одна точка тела остается все время неподвижной. Все точки тела движутся по траекториям, расположенным на поверхностях сфер, описанных из неподвижной точки.
Как известно, свободное тело в пространстве имеет шесть степеней свободы, а закрепление одной точки уменьшает это число на три. Таким образом, тело, вращающееся вокруг неподвижной точки, имеет всего три степени свободы. Для определения его положения необходимо иметь три независимые величины.
Наибольшее применение получили углы Эйлера.
Через неподвижную точку О твердого тела проведем неподвижную систему координат 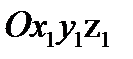 , относительно которой рассматриваем движение тела
, относительно которой рассматриваем движение тела
(рис. 15.1). Подвижную систему координат 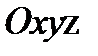 жестко скрепим с телом.
жестко скрепим с телом.
Положение подвижной системы координат относительно неподвижной, то есть положение тела, будем характеризовать следующими тремя углами Эйлера.
|
|
|
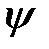 – угол прецессии, то есть угол между осью
– угол прецессии, то есть угол между осью  и линией узлов ОК (линия пересечения подвижной координатной плоскости
и линией узлов ОК (линия пересечения подвижной координатной плоскости  с неподвижной
с неподвижной  ). Этим углом определяется вращение тела вокруг неподвижной оси
). Этим углом определяется вращение тела вокруг неподвижной оси  , называемой осью прецессии. Положение линии узлов ОК изменяется одновременно относительно подвижной и неподвижной систем координат
, называемой осью прецессии. Положение линии узлов ОК изменяется одновременно относительно подвижной и неподвижной систем координат 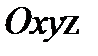 и
и  .
.
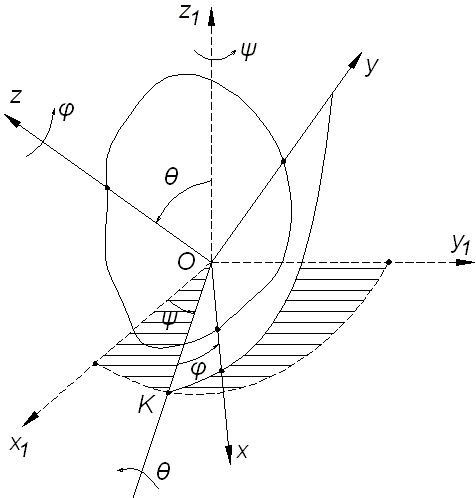
| Рис. 15.1 |
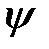 между положительными направлениями оси
между положительными направлениями оси 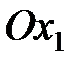 и линии узлов ОК считается положительным при его отсчете против часовой стрелки, если смотреть с конца оси
и линии узлов ОК считается положительным при его отсчете против часовой стрелки, если смотреть с конца оси 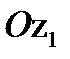 . Положительным направлением линии узлов ОК считается то, при котором, глядя с конца ее, можно видеть поворот оси
. Положительным направлением линии узлов ОК считается то, при котором, глядя с конца ее, можно видеть поворот оси 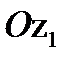 до совмещения с осью
до совмещения с осью 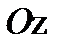 кратчайшим путем против часовой стрелки.
кратчайшим путем против часовой стрелки.
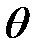 - угол нутации, то есть двугранный угол между координатными плоскостями
- угол нутации, то есть двугранный угол между координатными плоскостями 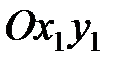 и
и  , определяемый как угол между перпендикулярными к этим плоскостям координатными осями
, определяемый как угол между перпендикулярными к этим плоскостям координатными осями  и
и  . Он считается положительным, если его отсчет с конца линии узлов ОК виден против часовой стрелки. Поэтому линию узлов ОК называют осью нутации.
. Он считается положительным, если его отсчет с конца линии узлов ОК виден против часовой стрелки. Поэтому линию узлов ОК называют осью нутации.
 - угол собственного вращения, то есть угол между осью координат
- угол собственного вращения, то есть угол между осью координат  и положительным направлением линии узлов ОК. Он считается положительным, если с конца оси
и положительным направлением линии узлов ОК. Он считается положительным, если с конца оси  , перпендикулярной к плоскости, образованной прямыми ОК и
, перпендикулярной к плоскости, образованной прямыми ОК и  , поворот от ОК до
, поворот от ОК до  виден против часовой стрелки. Ось
виден против часовой стрелки. Ось  называется осью собственного вращения.
называется осью собственного вращения.
При вращении тела вокруг неподвижной точки в общем случае одновременно изменяются все углы Эйлера  ,
,  ,
,  . Однако из одного в другое положение тело можно переместить, меняя углы Эйлера не все одновременно, а последовательно в любом порядке. Изменения углов
. Однако из одного в другое положение тело можно переместить, меняя углы Эйлера не все одновременно, а последовательно в любом порядке. Изменения углов  ,
,  ,
,  для двух рассматриваемых положений тела будут такими же, как и при одновременном их изменении. Поэтому углы Эйлера являются независимыми параметрами или обобщенными координатами, характеризующим и положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера является необходимым и достаточным условием для полного описания движения тела с одной закрепленной точкой.
для двух рассматриваемых положений тела будут такими же, как и при одновременном их изменении. Поэтому углы Эйлера являются независимыми параметрами или обобщенными координатами, характеризующим и положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера является необходимым и достаточным условием для полного описания движения тела с одной закрепленной точкой.
Эти углы изменяются со временем и могут быть описаны зависимостями
 ,
,  ,
,  (15.1).
(15.1).
Уравнения (15.1) называются кинематическими уравнениями вращения твердого тела вокруг неподвижной точки. С их помощью можно определить положение твердого тела относительно неподвижной системы координат  в любой момент времени.
в любой момент времени.
|
|
|
Билет№3

| I |
| II |
| Рис. 15.2 |
Доказательство
Построим сферическую поверхность с центром в точке О (рис. 15.2). Отметим положения двух точек А и В на этой сфере, характеризующих положение тела I, и положения  и
и 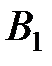 , характеризующих положения тела II. Дуги
, характеризующих положения тела II. Дуги  и
и  принадлежат сфере.
принадлежат сфере.
Соединим точку  с
с  и
и 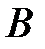 с
с  дугами большего круга (они лежат в плоскостях точек
дугами большего круга (они лежат в плоскостях точек  ,
,  ,
,  и
и  ,
,  ,
,  ). В серединах дуг
). В серединах дуг 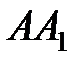 и
и  отмечаем точки
отмечаем точки  и
и  , из которых проводим сферические перпендикуляры, то есть дуги большого круга СР и DP (их касательные в точках С и D перпендикулярны к касательным к дугам
, из которых проводим сферические перпендикуляры, то есть дуги большого круга СР и DP (их касательные в точках С и D перпендикулярны к касательным к дугам  и
и  в тех же точках).
в тех же точках).
Эти перпендикуляры пересекаются в точке Р. Заметим, что сферические прямоугольные треугольники 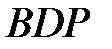 и
и 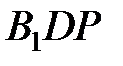 равны между собой, так как имеют общий катет
равны между собой, так как имеют общий катет  и равные катеты
и равные катеты 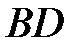 и
и  . Таким образом, в них равны и гипотенузы
. Таким образом, в них равны и гипотенузы  , то есть точки
, то есть точки  и
и  равноудалены от точки Р.
равноудалены от точки Р.
Можно доказать равноудаленность точек  и
и  от точки Р (
от точки Р ( ).
).
Если повернуть заштрихованный сферический  вокруг оси
вокруг оси  , то он, перемещаясь по сфере, совпадет с равным ему сферическим треугольником
, то он, перемещаясь по сфере, совпадет с равным ему сферическим треугольником  , так как сферический угол, на который надо повернуть вокруг ОР дугу АР до совпадения с дугой
, так как сферический угол, на который надо повернуть вокруг ОР дугу АР до совпадения с дугой 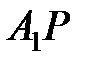 , равен сферическому углу на той же сфере, на который надо повернуть дугу ВР до совпадения с дугой
, равен сферическому углу на той же сфере, на который надо повернуть дугу ВР до совпадения с дугой  .
.
Таким образом, путем поворота вокруг оси, перпендикулярной к поверхности сферы и проходящей через точку Р и, следовательно, через неподвижную точку тела, тело можно переместить из одного положения в другое. Заметим, что точка Р и, следовательно, конечная ось вращения соответствуют выбранным двум положениям тела.
|
|
|


