Преобразование параллельного соединения ветвей с источниками ЭДС и источниками тока

 

Если сложная электрическая схема имеет одну или несколько групп параллельно соединенных ветвей с источниками ЭДС, то расчет такой схемы можно значительно облегчить, заменив каждую группу параллельных ветвей одним источником с эквивалентной ЭДС и эквивалентным внутренним сопротивлением.

На рис. 1.4,а показана группа из m параллельно соединенных ветвей, выделенная в электрической схеме. Остальная часть схемы обозначена прямоугольником.

Требуется заменить параллельные ветви одной эквивалентной ветвью (рис. 1.4,б) так, чтобы ток I и напряжение U в эквивалентной схеме, а значит, все токи и напряжения в остальной части схемы были такими же, как в заданной.

Для токов ветвей и суммарного тока I схемы на рис. 1.4,а справедливо выражение:

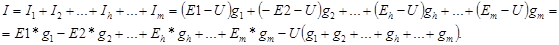(1.15)

В схеме на рис. 4,б

. (1.16)

Т.к. условия эквивалентности должны быть выполнены при любых токе I и напряжении U, то, приравнивая правые части выражений (1.15), (1.16), нужно положить:

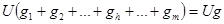; (1.17)

. (1.18)

 

а) б)

 

Рисунок 1.4

 

Тогда

; (1.19)

. (1.20)

При вычислении эквивалентной ЭДС Е с положительным знаком записываются те ЭДС, которые направлены к тому же узлу, что и эквивалентная ЭДС, и с отрицательным знаком – направленные к другому узлу. Если какая-либо ветвь не содержит источник ЭДС, то в числителе выражения (1.20) она не учитывается, но в состав проводимости g ее проводимость входит.

Эквивалентная проводимость g не зависит от ЭДС, в то время как эквивалентная ЭДС Е зависит не только от ЭДС ветвей, но и от их проводимостей.

Несмотря на неизменность токов и напряжений в той части схемы, которая не затронута преобразованием, мощность, развиваемая источниками ЭДС до преобразования, не равна мощности, развиваемой эквивалентным источником ЭДС после преобразования схемы.

Если к узлам 1 и 2 (рис. 1.4,а) присоединены кроме m ветвей с источниками ЭДС еще n ветвей с источниками тока, то при вычислении эквивалентной ЭДС нужно учесть токи заданных источников тока:

. (1.21)

 

Принцип наложения

При рассмотрении метода контурных токов было получено выражение для определения контурных токов

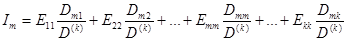. (1.22)

Если в уравнении (1.22) заменить все контурные ЭДС алгебраическими суммами ЭДС ветвей, то после группировки слагаемых получится выражение для контурного тока I_m в виде алгебраической суммы составляющих токов, вызванных каждой их ЭДС ветвей в отдельности. При этом каждая составляющая тока равна произведению ЭДС ветви на алгебраическую сумму коэффициентов вида , входящих в уравнение (1.22).

Это важное свойство носит название принципа наложения и непосредственно вытекает из линейности уравнений электрического состояния для цепей с линейными элементами. Принцип наложения справедлив не только для контурных токов, но и для токов ветвей, так как систему независимых контуров всегда можно выбрать так, что рассматриваемая ветвь войдет только в один контур, т.е. контурный ток будет равен действительному току ветви.

Рассмотрим электрическую схему, приведенную на рис. 1.5.

 

 

Рисунок 1.5

 

Пользуясь методом контурных токов, запишем следующие уравнения:

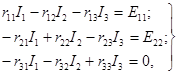(1.23)

где

;

Из уравнений (1.23):

, (1.24)

где

; ; ;

; .

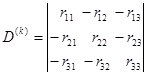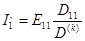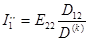Аналогично определяются токи I₂ и I₃.

Если в выражении (1.24) контурные ЭДС заменить через ЭДС ветвей, то получим:

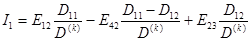. (1.25)

Из выражения (1.25) следует, что контурный ток I₁ равен алгебраической сумме составляющих токов, вызываемых каждой из ЭДС в отдельности. Кроме того, этот контурный ток равен действительному току ветви с сопротивлением r₁ и ЭДС Е₁₂, так как по этой ветви другие контурные токи не замыкаются.

Таким образом, при определении токов ветвей при помощи принципа наложения можно поочередно оставлять в схеме по одной ЭДС, считая все остальные ЭДС источников равными нулю, но сохраняя в схеме их внутренние сопротивления. Действительные токи ветвей определятся как алгебраические суммы токов, вызываемых каждой ЭДС. Если схема содержит не только источники ЭДС, но и источники тока, то следует найти составляющие токов, вызываемые каждой ЭДС и каждым источником тока, посте чего определить действительные токи путем алгебраического суммирования этих составляющих.

В применении к электрическим цепям можно определять не только токи по заданным ЭДС и сопротивлениям, но и напряжения по заданным токам и известным сопротивлениям. Однако этим принципом нельзя пользоваться для вычисления мощностей, так как мощность – квадратичная функция тока или напряжения.

 

Свойство взаимности

 

Пользуясь методом контурных токов можно установить еще одно важное свойство линейных электрических цепей – свойство взаимности (принцип взаимности).

Пусть в схеме произвольной конфигурации единственный источник ЭДС E_q действует в ветви с сопротивлением r_q в направлении от точки b к точке а (рис. 1.6,а) и создает в ветви с сопротивлением r_k ток I_k, направленный от точки d к точке с.

Тогда такой же единственный источник ЭДС E_k = E_q, включенный в ветвь с сопротивлением r_k и действующий в направлении от d к c (рис. 1.6,б), создаст в ветви с сопротивлением r_q ток I_q, направленный от b к а и равный току I_k.

На рис. 1.6,а изображены ветви ab и cd с сопротивлениями r_q и r_k, а остальная часть схемы, не содержащая источники энергии, условно показана в виде прямоугольника с буквой П (пассивная).

Для доказательства свойства взаимности воспользуемся выражением, определяющем ток в любом контуре. Пусть ветвь cd является частью контура k, а ветвь ab входит в состав другого контура q и, как указано, других источников ЭДС, кроме Е_q, эта цепь не содержит. Контуры выберем так, чтобы ветви ab и cd вошли каждая в свой контур, соответственно q и k.

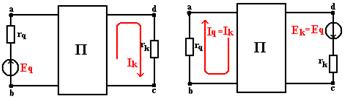
а) б)

 

Рисунок 1.6

 

Тогда ток I_k в контуре k, равный току ветви dc, определится выражением

. (1.26)

Если источник ЭДС Е_q переставить в ветвь cd контура k (рис. 1.6,б), то после этого ток I_q в контуре q, т.е. ток ветви ab, определится выражением

. (1.27)

Алгебраическое дополнение вида D_kq получается из определителя D^(m) путем вычеркивания в нем столбца k и строки q и умножения получаемого определителя на (-1)^k+q, а алгебраическое дополнение вида D_qk – вычеркиванием столбца q и строки k и умножением получаемого определителя на (-1)^q+k. Так как в контурных уравнениях общие сопротивления r_qk и r_kq равны друг другу, то и D_kq = D_qk. Следовательно, при равенстве ЭДС E_q = E_k токи в ветвях cd и аb равны друг другу.

 

Теорема о компенсации

В электрической схеме, показанной на рис. 1.7,а, выделена ветвь с сопротивлением r₁ и током I₁.

 

а) б) в)

 

Рисунок 1.7

Включим в эту ветвь два источника ЭДС Е1^́ и Е1 (рис. 1.7,б), численно равными напряжению U₁ = r₁I₁ и направленными навстречу друг другу. Очевидно, что при этом токи во всех ветвях схемы не изменятся. При переходе из точки d в точку с потенциал повышается на величину ЭДС Е1^́ = U₁, а при переходе из точки с в точку b понижается на ту же величину, вследствие чего потенциалы точек d и b равны. Эти точки можно закоротить, как показано на рисунке 1,б синей линией, т.е. источник ЭДС Е1^́ = U₁ и сопротивление r₁ удалить из схемы, не изменив токи во всех ветвях (рис. 1.7,в).

Из сравнения схем на рис. 1.7,а и 1.7,в следует, что любое сопротивление можно заменить источником ЭДС, направленной навстречу току и равной напряжению на этом сопротивлении. Это положение называется теоремой о компенсации.

 

Двухполюсники

При исследовании процессов в сложных электрических цепях часто необходимо определить ток, напряжение и мощность только в одной ветви. В этом случае выделяется ветвь, присоединенная к сложной цепи в двух точках. Часть электрической цепи произвольной конфигурации с двумя выделенными зажимами, именуемыми полюсами, называется двухполюсником.

Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источники электрической энергии,- пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной – сопротивлением r_в. Поэтому на эквивалентной схеме пассивный двухполюсник может быть представлен одним элементов – сопротивлением r_в, называемым внутренним или входным сопротивлением пассивного двухполюсника.

Если известна схема пассивного двухполюсника, то для определения входного сопротивления r_в нужно тем или иным способом ее «свернуть» относительно двух заданных режимов.

Рассмотрим схему на рис. 1.8,а.

 

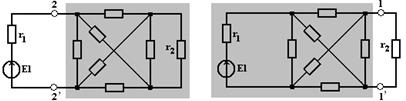
а) б)

 

Рисунок 1.8

 

Если выделить в этой схеме ветвь с источником Е1 и сопротивлением r₁, то остальную часть схемы можно рассматривать относительно зажимов 2-2́ как пассивный двухполюсник. Часть той же схемы относительно зажимов 1-1́ ветви с сопротивлением r₂ можно рассматривать как активных двухполюсник.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: